2023-2024学年北师大版数学八年级上册5.5应用二元一次方程组——里程碑上的数同步练习（培优卷）

试卷更新日期：2023-11-27 类型：同步测试

进入出卷网下载

一、选择题

1. 小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路．她去学校共用了16分钟．假设小颖上坡路的平均速度是3千米/时，下坡路的平均速度是5千米/时，若设小颖上坡用了x分钟，下坡用了y分钟，根据题意可列方程组为（　　）

A、 ${\begin{array}{l} 3 x + 5 y = 1200 \\ x + y = 16 \end{array}$ B、 ${\begin{array}{l} \frac{3}{60} x + \frac{5}{60} y = 1.2 \\ x + y = 16 \end{array}$ C、 ${\begin{array}{l} 3 x + 5 y = 1.2 \\ x + y = 16 \end{array}$ D、 ${\begin{array}{l} \frac{3}{60} x + \frac{5}{60} y = 1200 \\ x + y = 16 \end{array}$

查看试题解析
2. 为提高学生学习兴趣，增强动手实践能力，某校为物理兴趣小组的同学购买了一根长度为150cm的导线，将其全部截成10cm和20cm两种长度的导线用于实验操作（每种长度的导线至少一根），则截取方案共有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析
3. 一个两位数，十位上的数字比个位上的数字大2；交换十位上的数字与个位上的数字后得到的两位数比原数小18．设十位上的数字为x，个位上的数字为y，列方程组为（）

A、 ${\begin{array}{l} x - y = 2 \\ 10 x + y - (10 y + x) = 18 \end{array}$ B、 ${\begin{array}{l} x - y = 2 \\ 10 y + x - (10 x + y) = 18 \end{array}$ C、 ${\begin{array}{l} y - x = 2 \\ 10 y + x - (10 x + y) = 18 \end{array}$ D、 ${\begin{array}{l} y - x = 2 \\ 10 x + y - (10 y + x) = 18 \end{array}$

查看试题解析
4. 在一个3×3的方格中填写9个数字，使得每行每列每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．如图所示的方格中填写了一些数和字母，为使该方格构成一个三阶幻方，则x+2y的值是（）
﹣3
y

1

4
x

A、15 B、17 C、19 D、21

查看试题解析
5. 如图，长青化工厂与 $A$ ， $B$ 两地有公路、铁路相连．这家工厂从 $A$ 地购买一批每吨1000元的原料运回工厂，制成每吨6000元的产品运到 $B$ 地．公路运价为1.6元 $/ (t • k m)$ ，铁路运价为1.2元 $/ (t • k m)$ ，这两次运输共支出公路运费16000元，铁路运费97200元．这批产品的销售款比原料费与运输费的和多（）元．

A、1286800 B、299000 C、1286000 D、298000

查看试题解析

6. 爸爸骑摩托车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数如下：

时刻	9：00	10：00	11：30
里程碑上的数	是一个两位数，它的两个数字之和是6	是一个两位数，它的十位与个位数字与9：00所看到的正好互换了	是一个三位数，它比9：00时看到的两位数中间多了个0

则10：00时看到里程碑上的数是（）

A、15 B、24 C、42 D、51

查看试题解析

7. 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 ${\begin{cases} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{cases}$ ，在图2所示的算筹图中有一个图形被墨水覆盖了，如果图2所表示的方程组中x的值为3，则被墨水所覆盖的图形为（）

A、| B、|| C、||| D、||||

查看试题解析

8. 爸爸开车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数如下

时刻	9：00	9：45	12：00
碑上的数	是一个两位数，数字之和是9	十位与个位数字与9：00时所看到的正好相反	比9：00时看到的两位数中间多了个0

9：00时看到的两位数是（）

A、54 B、45 C、36 D、27

查看试题解析

9. 有一个两位数和一个一位数，它们的和为39，若将两位数放在一位数的前面，得到的三位数比将一位数放在两位数的前面得到的三位数大27，求这两个数．若设两位数是x，一位数是y，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 39 \\ x y - y x = 27 \end{array}$ B、 ${\begin{array}{l} x + y = 39 \\ 10 x + y + 27 = 100 y + x \end{array}$ C、 ${\begin{array}{l} x + y = 39 \\ 10 x + y - 27 = 10 y + x \end{array}$ D、 ${\begin{array}{l} x + y = 39 \\ 10 x + y - (100 y + x) = 27 \end{array}$

查看试题解析
10. 甲、乙两地相距60千米，一艘轮船往返两地，顺流用2小时，逆流用3小时，那么这艘轮船在静水中的速度是（）

A、5千米/时 B、20千米/时 C、25千米/时 D、30千米/时

查看试题解析

二、填空题

11. 课余活动中，小杰、小明和小丽一起玩飞镖游戏，飞镖盘上A区域所得分值和B区域所得分值不同，每人投5次飞镖，其落点如图所示，已知小杰和小明的5次飞镖总分分别为39分和43分，小丽的5次飞镖总分为分．

查看试题解析
12. 江津花椒以“鲜香麻”闻名，深受重庆人民的喜爱．其中甲品种最麻，乙品种次之，丙品种最后．去年，江津某县种植的甲、乙、丙三种品种的面积之比为 2：3： 5．今年因需求量的增加，该县决定将其种植面积扩大．计划将扩大部分的 $\frac{3}{8}$ 用于种植丙品种，则丙品种的种植面积将达到这三种花椒种植总面积的 $\frac{4}{9}$ ；扩大部分的剩余面积全部用于种植甲品种和乙品种，为了使甲品种的种植面积与乙品种的种植面积之比达到 $4 ： 3$ ，则该县种扩大种植甲品种的面积与该县种植这三种花椒的总面积之比是．

查看试题解析
13. 对于一个三位数 $n$ ，如果 $n$ 满足∶ 它的百位数字、十位数字之和与个位数字的差等于 7 ，那么称这个数 $n$ 为 “幸福数”. 例如∶ $n_{1} = 722 ， ∵ 7 + 2 - 2 = 7 ， ∴ 722$ 是“幸福数”； $n_{2} = 913 ， ∵ 9 + 1 - 3 = 7 ， ∴ 913$ 是“幸福数”； $n_{3} = 285 ， ∵ 2 + 8 - 5 \neq 7 ， ∴ 285$ 不是“幸福数”. 若将一个“幸福数” $m$ 的个位数的 2 倍放到十位，原来的百位数变成个位数，原来的十位数变成百位数，得到一个新的三位数 $t$ (例如∶ 若 $m = 654$ ，则 $t = 586$ )，若 $t$ 也是一个“幸福数”，则满足条件的所有 $m$ 的值.

查看试题解析
14. 如图所示的两架天平保持平衡，且每块巧克力的质量相等，每个果冻的质量也相等，则每块巧克力的质量为g．

查看试题解析
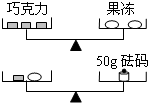15. “八月十五月儿圆，中秋月饼香又甜”，每中秋，皓月当空，阖家团聚，品饼赏月，谈天说地，尽享天伦之乐.今年中秋节前夕某商场结合当地情况，决定启动一笔专项资金用于月饼进货，经过一段时间，该商场已购进的京式、广式、苏式月饼总价之比为2：3：4，根据市场需求，将把余下的资金继续购进这三种月饼，经测算需将余下资金的 $\frac{1}{3}$ 购买京式月饼，则京式月饼的总价将达到这三种月饼总价的 $\frac{4}{15}$ .为了使广式月饼总价与苏式月饼的总价达到9：13，则该商场还需购买的广式月饼总价与苏式月饼的总价之比是.

查看试题解析

三、综合题

16. 如图，在 $3 \times 3$ 的方格内，填写了一些代数式和数．

(1)、在图1中各行、各列及对角线上三个数之和都相等，请你求出 $x$ ， $y$ 的值；

(2)、把满足（1）的其它6个数填入图2中的方格内．

查看试题解析
17. 娄底市出租车收费规定：起步价所包含的路程为0～1.5千米，超过1.5千米的部分按每千米另收费．
刘同学说：“我乘出租车从市政府到娄底汽车站走了4.5千米，付车费11元．”
李同学说：“我乘出租车从市政府到娄底火车站走了6.5千米，付车费15元．”
问：

(1)、出租车的起步价是多少元？超过1.5千米后每千米收费多少元？

(2)、小张乘出租车从家里到娄底南站（高铁站）走了9.5千米，应付车费多少元？

查看试题解析
18. 某公司在手机网络平台推出的一种新型打车方式受到大众的欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/千米计算，耗时费按y元/分钟计算．小聪、小明两人用该打车方式出行，按上述计价规则，他们打车行驶里程数、所用时间及支付车费如下表：

里程数（千米）

时间（分钟）

车费（元）

小聪

3

10

9

小明

6

18

17.4

(1)、求x ， y的值；

(2)、该公司现推出新政策，在原有付费基础上，当里程数超过8千米后，超出的部分要加收0.6元/千米的里程费，小强使用该方式从家打车到郊区，总里程为23千米，耗时30分钟，求小强需支付多少车费．

查看试题解析
19. 如图， $A$ ， $B$ 两地由公路和铁路相连，在这条路上有一家食品厂，它到 $B$ 地的距离是到 $A$ 地距离的 $2$ 倍，现该食品厂从 $A$ 地购买原料，全部制成食品制作过程中有损耗 $)$ 卖到 $B$ 地，两次运输 $($ 第一次： $A$ 地 $\to$ 食品厂，第二次：食品厂 $\to B$ 地 $)$ 共支出公路运费 $15600$ 元，铁路运费 $20600$ 元．已知公路运费为 $1.5$ 元 $/ ($ 千米 $\cdot$ 吨 $)$ ，铁路运费为 $1$ 元 $/ ($ 千米 $\cdot$ 吨 $)$ ．

(1)、求该食品厂到 $A$ 地， $B$ 地的距离分别是多少千米？

(2)、求该食品厂买进原料及卖出食品各多少吨？

(3)、若该食品厂此次买进的原料每吨花费5000元，要想该批食品销售完后工厂共获利863800元，求卖出的食品每吨售价是多少元？（利润 $=$ 总售价 $-$ 总成本 $-$ 总运费）

查看试题解析
20. 下面是学习二元一次方程组时，老师提出的问题和两名同学所列的方程.
问题：某个工人一天工作6个小时，可以生产零件一整箱和不足一箱的20个；由于特殊情况，今天他只工作4个小时，生产零件一整箱和不足一箱的4个，问这一箱零件和该工人每小时能生产的零件数分别是多少？
小明所列方程： ${\begin{array}{l} 6 y = x + 20 \\ 4 y = x + 4 \end{array}$ 小亮所列方程： $\frac{4 (x + 20)}{6} = x + 4$
根据以上信息，解答下列问题.

(1)、以上两个方程（组）中x意义是否相同？（填“是”或“否”）；

(2)、小亮的方程所用等量关系（填序号，“①每个小时生产的零件数”或“②4个小时生产的零件数相等”）；

(3)、从以上两个方程（组）中任选一个求解，完整解答老师提出的问题.

查看试题解析
21. 一个n位数（ $n \geq 2$ ，n为正整数），我们把最高位上的数移到它的右侧，得到一个新数，再将新数的最高位上的数移到它的右侧，又得到一个新数，…，依次类推，我们把这样操作得到的新数都叫做原数的“谦虚数”.比如56有一个“谦虚数”是65；156有两个“谦虚数”分别是561、615；2834有三个“谦虚数”分别是8342、3428、4283.

(1)、请写出四位数5832的三个“谦虚数”.

(2)、一个两位数，个位上的数与十位上的数和为9，如果这个两位数比它的“谦虚数”少9，求这个两位数.

(3)、一个三位数，百位上的数为a，十位上的数为1，个位上的数为b，如果这个三位数与它的两个“谦虚数”的和能被5整除，求 $a + b$ 的值.

查看试题解析

	里程数（千米）	时间（分钟）	车费（元）
小聪	3	10	9
小明	6	18	17.4

﹣3	y
	1
4		x

2023-2024学年北师大版数学八年级上册5.5应用二元一次方程组——里程碑上的数 同步练习（培优卷）

一、选择题

二、填空题

三、综合题

2023-2024学年北师大版数学八年级上册5.5应用二元一次方程组——里程碑上的数同步练习（培优卷）