浙江省丽水市龙泉市2023-2024学年七年级第一学期数学期中考试试卷

试卷更新日期：2023-11-27 类型：期中考试

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分)

1. 实数2的相反数是（）

A、 $\frac{1}{2}$ B、-2 C、 $- \frac{1}{2}$ D、2

查看试题解析
2. 下列四个数中，最小的数是（）

A、-1 B、0 C、3 D、 $\sqrt{2}$

查看试题解析
3. 据世卫组织统计数据，至2022年10月8日，全球累计新冠确诊病例约6180000000例，6180000000用科学记数法可表示为（）

A、 $61.8 \times 1 0^{7}$ B、 $6.18 \times 1 0^{8}$ C、 $0.618 \times 1 0^{10}$ D、 $6.18 \times 1 0^{9}$

查看试题解析
4. 某天，厦门的最低气温 $1 5^{°} C$ ，哈尔滨的最低气温是 $- 1^{°} C$ ，这天两个城市的最低气温相差（）

A、 $1 4^{°} C$ B、 $1 5^{°} C$ C、 $1 6^{°} C$ D、 $1 7^{°} C$

查看试题解析
5. 单项式 $- 15 x^{2} y$ 的系数和次数分别是（）

A、 $- 15 ， 3$ B、 $- 15 ， 2$ C、15，3 D、15，2

查看试题解析
6. 下列运算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt[3]{- 27} = - 3$ C、 $- 2^{2} = 4$ D、 $(- 2)^{3} = - 6$

查看试题解析
7. 一台冰箱的原价是4000元，先提价 $10 %$ ，再打九折销售.则这台冰箱现在的价格和原来的价格比（）

A、提高了 B、不变 C、降低了 D、无法确定

查看试题解析
8. 已知 $| a - 1 | + \sqrt{3 - b} = 0$ ，则 $a + b$ 的值为（）

A、-4 B、-2 C、2 D、4

查看试题解析
9. 如图，面积为2的正方形ABCD的顶点 $A$ 在数轴上，以 $A$ 为圆心，AB为半径画弧交数轴于点 $E$ ，点 $E$ 表示的数为 $\sqrt{3}$ ，则点 $A$ 表示的数是（）

A、 $- \sqrt{3}$ B、 $\sqrt{2}$ C、 $\sqrt{3} - 1$ D、 $\sqrt{3} - \sqrt{2}$

查看试题解析
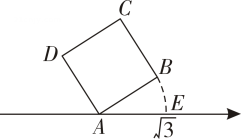10. 一个自然数，把它各数位上的数字从最高位到个位依次排列得到一串数字，再把它各数位上的数字从个位到最高位依次排列，得到另一串数字，如果两串数字完全相同，我们就把这样的自然数称为“回文数”.例如22，323，4664，567765等都是“回文数”.已知一个三位数是能被11整除的“回文数”，则符合条件的三位数的个数有（）

A、4个 B、9个 C、24个 D、33个

查看试题解析

二、填空题(本题有6小题,每小题4分,共24分)

11. -5的倒数是.

查看试题解析
12. 将3.14159精确到0.01的近似值为.

查看试题解析
13. 用代数式表示“a的平方与b的2倍的和”是.

查看试题解析
14. 数轴上在原点右侧，且到原点距离为3个单位长度的点所表示的数是.

查看试题解析
15. 定义“★”是一种新运算，对于任意有实数，a，b（a≠b）.当a＞b时， $a ★ b = a^{2} - b$ ；当 $a < b$ 时， $a ★ b = a - b^{2}$ .例如： $2 ★ 1 = 2^{2} - 1 = 3 ，$ $1 ★ 2 = 1 - 2^{2} = - 3$ ，那么 $2 ★ [(- 2) ★ (- \sqrt{3})] =$ .

查看试题解析
16. 如图1，一个边长为6的正方形被分割成四个完全相同的直角三角形和一个阴影小正方形(无缝隙、不重叠)，现将这四个直角三角形分别沿着正方形四条边向外翻折，翻折后得到图2所示的大正方形.

(1)、若阴影小正方形的边长为1，则图2中大正方形的面积为.

(2)、若图2中大正方形的边长为正整数，则阴影小正方形的边长为.

查看试题解析

三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分，第22,23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)

17. 计算：

(1)、7+(-3)

(2)、3x(-2)

查看试题解析
18. 计算：

(1)、 $\sqrt[3]{- 64} + \sqrt{16} + | - 2 |$

(2)、 $(- 6)^{2} \times (\frac{2}{3} - \frac{1}{2})$

查看试题解析
19. 在数轴上表示下列各数，并把这些数按从小到大的顺序排列，用“<”连接.
-1，0， $- \frac{3}{2}$ ， $\frac{1}{2}$ ， 3.

查看试题解析
20. 把下列各数填入相应括号里： $3.1 \overset{•}{4}$ ， -2，0，-0.01001， $- \frac{1}{2}$ ， $π$ ， $\sqrt{3}$ ， $\frac{22}{7}$
负分数：（）；整数：（）；无理数：（）；正有理数：（）.

查看试题解析
21. 在2023年杭州亚运会上，我国获得金牌总数又突破历史新高.其中赛程前5日，如果以每日获20枚金牌为基准，记超过20枚的金牌数为正.获金牌情况如下表所示：
日期
9月24日
9月25日
9月26日
9月27日
9月28日
金牌数(枚)
0
-1
-6
3
-6

(1)、前5日我国总共获得几枚金牌?

(2)、在剩下的赛程中，我国获得金牌数是前5日总共获得金牌数的 $\frac{4}{3}$ 倍少9枚，求这届亚运会上我国共获得多少枚金牌?

查看试题解析
22. 2023年10月26日，“神州十七号”飞船成功出征太空.同学们倍受鼓舞，某同学绘制了如图所示的火箭模型截面图，上面是三角形，中间是长方形，下面是梯形.

(1)、用含有x，y的代数式表示该截面的面积S；

(2)、当x=3，y=2时，求这个截面的面积.

查看试题解析
23. 阅读材料：我们知道，4x-2x+x=(4-2+1)x=3x，类似地，我们把(a+b)看成一个整体，则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).“整体思想”是数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛。尝试应用整体思想解决下列问题：

(1)、把 $(a - b)^{2}$ 看成一个整体，合并 $2 (a - b)^{2} - 6 (a - b)^{2} + 3 (a - b)^{2}$ ；

(2)、若 $a (x^{2} - 2 y) + b (x^{2} - 2 y)$ $= x^{2} - 2 y$ ，且 $x^{2} - 2 y \neq 0$ ，求 $a + b + 2023$ 的值；

(3)、若对于任意 $x$ 都有 $(a x^{5} + b x^{4} + x^{3} + x^{2} + x) +$ $(c x^{5} + c x^{4} + x^{3} + x^{2} + x) =$ $2 (x^{3} + x^{2} + x)$ 成立，且 $a b c d \neq 0$ ，比较 $\frac{c}{a}$ 与 $\frac{d}{b}$ 的大小，并说明理由.

查看试题解析
24. 如图，数轴上从左到右排列的A，B，C三点的位置如图所示.点B表示的数是3，A和B两点间的距离为8，B和C两点间的距离为4.

(1)、求A，C两点分别表示的数；

(2)、若动点P从点A出发，以每秒2个单位长度的速度向右运动，运动时间为t秒.
①当点P运动到与点B和点C的距离相等时，求t的值；
②若同时，有M，N两动点分别从点B，C同时出发，都以每秒1个单位长度的速度沿着数轴向左运动，把点P与点M之间的距离表示为PM，点P与点N之间的距离表示为PN，当PM+PN取最小值时，求t的最大值和最小值.

查看试题解析

日期	9月24日	9月25日	9月26日	9月27日	9月28日
金牌数(枚)	0	-1	-6	3	-6