浙江省湖州市安吉县2023-2024学年八年级第一学期数学期中阶段性检测试卷
试卷更新日期:2023-11-27 类型:期中考试
一、仔细选一选(本题有10个小题,每小题3分,共30分)
-
1. 下列四组线段中,能组成三角形的是 ( )A、2cm,3 cm,4 cm B、3 cm,4 cm,7 cm C、4 cm,6 cm,2 cm D、7 cm,10 cm,2 cm2. 如图,下列图案是我国几家银行的标志,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 > C、x+3>y+3 D、-3x>-3y4. 下列对△ABC的判断,错误的是( )A、若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 B、若∠A=30°,∠B=50°,则△ABC是锐角三角形 C、若AB=AC,∠B=40°,则△ABC是钝角三角形 D、若2∠A=2∠B=∠C,则△ABC是等腰直角三角形5. 在数轴上表示不等式x≥-2的解集,正确的是( )A、
3. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 > C、x+3>y+3 D、-3x>-3y4. 下列对△ABC的判断,错误的是( )A、若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 B、若∠A=30°,∠B=50°,则△ABC是锐角三角形 C、若AB=AC,∠B=40°,则△ABC是钝角三角形 D、若2∠A=2∠B=∠C,则△ABC是等腰直角三角形5. 在数轴上表示不等式x≥-2的解集,正确的是( )A、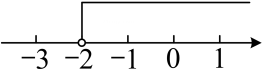 B、
B、 C、
C、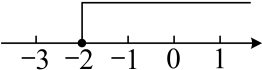 D、
D、 6. 如图,尺规作图,作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )
6. 如图,尺规作图,作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )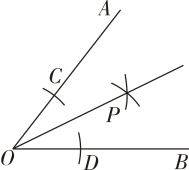 A、SAS B、ASA C、AAS D、SSS7. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1 , S2 , S3 , S4 . 若S1=48,S2+S3=135,则S4=( )
A、SAS B、ASA C、AAS D、SSS7. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1 , S2 , S3 , S4 . 若S1=48,S2+S3=135,则S4=( )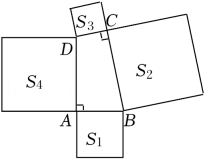 A、183 B、87 C、119 D、818. 直角三角形的两条边长分别是5和12,则斜边上的中线长是( )A、6.5 B、6 C、6或2.5 D、6或6.59. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于,则DE的长为( )
A、183 B、87 C、119 D、818. 直角三角形的两条边长分别是5和12,则斜边上的中线长是( )A、6.5 B、6 C、6或2.5 D、6或6.59. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于,则DE的长为( )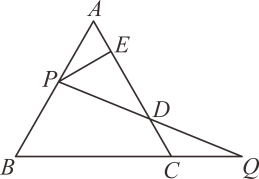 A、 B、 C、 D、10. 如图是一张长方形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF、EF,若MF=CD,则∠DAF的度数为( )
A、 B、 C、 D、10. 如图是一张长方形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF、EF,若MF=CD,则∠DAF的度数为( )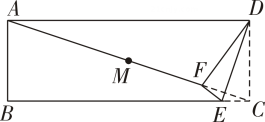 A、15° B、16° C、18° D、20°
A、15° B、16° C、18° D、20°二、认真填一填(本题有6个小题,每小题4分,共24分)
-
11. 命题:“两直线平行,则同旁内角互补”的逆命题为.12. 关于x的不等式2x+a≤0的解集如图所示,则a的值是.
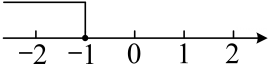 13. 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
13. 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是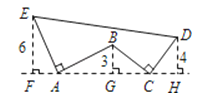 14. 如图,△ABC中,AB=AC,点D在AC上,点E在AB上,且AD=DE=EB,BD=BC,那么∠A= .
14. 如图,△ABC中,AB=AC,点D在AC上,点E在AB上,且AD=DE=EB,BD=BC,那么∠A= .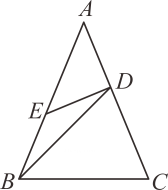 15. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AC=3、AB=5,则BD= .
15. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AC=3、AB=5,则BD= .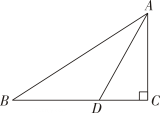 16. 如图,等腰Rt△ABC的直角边长为 , D,E分别为边AB,AC上两个动点,且AE=BD,则CD+BE的最小值.
16. 如图,等腰Rt△ABC的直角边长为 , D,E分别为边AB,AC上两个动点,且AE=BD,则CD+BE的最小值.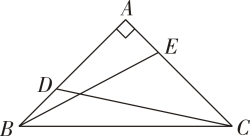
三、解答题(本题有8个小题,第17-19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,解答需写出必要文字说明、验算步骤或证明过程)
-
17. 在如图所示的正方形网格中,已有两个正方形涂黑,请再将其中的一个空白正方形涂黑,使整个图形是一个轴对称图形最少三种不同方法.
 18. 如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
18. 如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.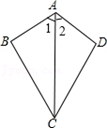 19. 如图,在△ABC中,AD,AE分别是边BC上的中线和高.
19. 如图,在△ABC中,AD,AE分别是边BC上的中线和高.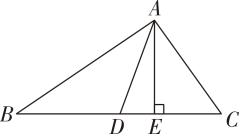 (1)、若AE=5cm,面积S△ABC=30cm2 , 求DC的长;(2)、若∠B=40°,∠C=50°,求∠DAE的大小.20. 如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE.求证:
(1)、若AE=5cm,面积S△ABC=30cm2 , 求DC的长;(2)、若∠B=40°,∠C=50°,求∠DAE的大小.20. 如图,△ABC中,AB=AC,AD⊥BC垂足为点D,CE⊥AB垂足为点E,AE=CE.求证: (1)、△AEF≌△CEB;(2)、AF=2CD.21. 若a、b是△ABC的两边且|a-3|+(b-4)2=0.(1)、试求a、b的值,并求第三边c的取值范围;(2)、若△ABC是等腰三角形,试求此三角形的周长.22. 某游乐场部分平面图如图所示,点C、E、A在同一直线上,点D、E、B在同一直线上,DB⊥AB.测得A处与E处的距离为80m,C处与E处的距离为40m,∠C=90°,∠BAE=30°.
(1)、△AEF≌△CEB;(2)、AF=2CD.21. 若a、b是△ABC的两边且|a-3|+(b-4)2=0.(1)、试求a、b的值,并求第三边c的取值范围;(2)、若△ABC是等腰三角形,试求此三角形的周长.22. 某游乐场部分平面图如图所示,点C、E、A在同一直线上,点D、E、B在同一直线上,DB⊥AB.测得A处与E处的距离为80m,C处与E处的距离为40m,∠C=90°,∠BAE=30°.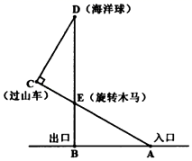 (1)、请求出旋转木马E处到出口B处的距离;(2)、请求出海洋球D处到出口B处的距离;(3)、判断入口A到出口B处的距离与海洋球D到过山车C处的距离是否相等?若相等,请证明;若不相等,请说明理由.23. 如图,B为∠A边上一点,AB=5,BC⊥AC,P为线段AC上一点,点Q,P关于直线BC对称,QD⊥AB于点D,直线DQ,BC交于点E,连结DP,设AP=m.
(1)、请求出旋转木马E处到出口B处的距离;(2)、请求出海洋球D处到出口B处的距离;(3)、判断入口A到出口B处的距离与海洋球D到过山车C处的距离是否相等?若相等,请证明;若不相等,请说明理由.23. 如图,B为∠A边上一点,AB=5,BC⊥AC,P为线段AC上一点,点Q,P关于直线BC对称,QD⊥AB于点D,直线DQ,BC交于点E,连结DP,设AP=m.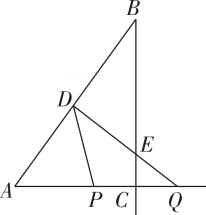 (1)、若BC=4,求用含m的代数式表示PQ的长;(2)、在(1)的条件下时,若AP=PD,求CP的长;(3)、连结PE,若∠A=60°,△PCE与△PDE的面积之比为1:2,求m的值.24. 【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,AD是△ABC的中线,若AB=5,AC=3,求AD的取值范围.
(1)、若BC=4,求用含m的代数式表示PQ的长;(2)、在(1)的条件下时,若AP=PD,求CP的长;(3)、连结PE,若∠A=60°,△PCE与△PDE的面积之比为1:2,求m的值.24. 【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,AD是△ABC的中线,若AB=5,AC=3,求AD的取值范围.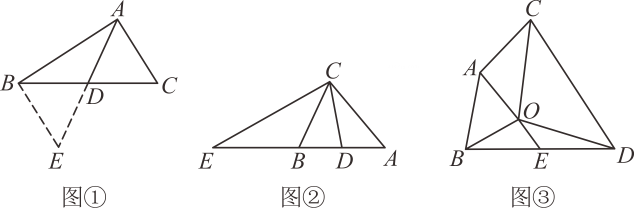 (1)、【探究方法】
(1)、【探究方法】小强所在的小组通过探究发现,延长AD至点E使ED=AD,连接BE.
可以证出△ADC≌△EDB,利用全等三角形的性质可将已知的边长与AD转化到到△ABE中,进而求出AD的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线AD延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
请你利用上面解答问题的思路方法,求出求AD的取值范围的过程.
(2)、【问题解决】如图②,CB是△AEC的中线,CD是△ABC的中线,且AB=AC,下列四个选项中:A.AC=BE B.CE=2CD C.∠BCD=∠BCE D.∠ACD=∠BCD.直接写出所有正确选项的序号是.
(3)、【问题拓展】如图③,在△ABO和△CDO中,OA=OB,OC=OD,∠AOB与∠COD互补,连接AC、BD,E是BD的中点,求证:OE=AC.