上海市复旦附高2023-2024学年高三上学期数学期中试卷

试卷更新日期：2023-11-27 类型：期中考试

进入出卷网下载

一、填空题(本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分)

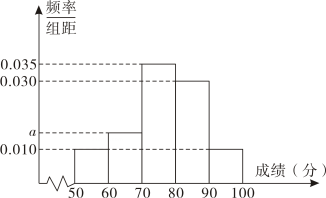
1. 已知复数 $z = \frac{1 - 2 i}{i}$ (i是虚数单位)，则z的虚部是.

查看试题解析
2. 已知3sinα=cosα，则tan(π-α)的值是.

查看试题解析
3. 已知某班全体学生在某次数学考试中的成绩(单位：分)的频率分布直方图如图所示，则图中a所代表的数值是.

查看试题解析
4. 已知两点P(3，4)，Q(-5，6)，则以线段PQ为直径的圆的标准方程是.

查看试题解析
5. 已知向量 $\vec{a} = (3, 4) ， \vec{b} = (1, 2) ，$ 则向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量的坐标为.

查看试题解析
6. 已知一个圆锥的轴截面是等边三角形，侧面积为8π，则该圆锥的体积等于.

查看试题解析
7. 齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马；田忌的下等马劣于齐王的下等马.现各从双方的马匹中随机选一匹进行一场比赛，则田忌的马获胜的概率为.

查看试题解析
8. 已知一组数据：10，11，12，13，13，14，15，16，记这组数据的第60百分位数为a，众数为b，则a和b的大小关系是.(用“<”，“>”，“=”连接)

查看试题解析
9. 已知函数f(x)=3sinx+2cosx，当f(x)取得最大值时， $t a n x$ =.

查看试题解析
10. 已知 $a^{l g a} b^{l g b} c^{l g e} = 5 ， a^{l g b} b^{l g c} c^{l g a} = \sqrt{2}$ 则abc的值为.

查看试题解析
11. 如图在△ABC中，AB=2，AC=5，∠BAC=60°，边BC、AC上的中线AM、BN相交于点P，则cos∠MPN=.

查看试题解析
12. 已知函数 $f (x) = l n x + 2 x ， g (x) = a x^{2} (a \in R, a \neq 0) ，$ 若有且仅有一个正整数 $x_{0} ，$ 使得不等式 $f (x_{0}) > g (x_{0})$ 成立，则实数a的取值范围是.

查看试题解析

二、选择题(本大题共有4题,13、14每题4分,15、16每题5分,满分18分)

13. 设ab>0，则“a>b”是 $“ \frac{1}{a} < \frac{1}{b} ”$ 的（）.

A、充分非必要条件 B、必要非充分条件 C、充分必要条件 D、既非充分也非必要条件

查看试题解析
14. 定义在区间(-∞，0)∪(0，+∞)的函数f(x)，如果对于任意给定的非常数等比数列{an}，{f(an)}仍是等比数列，则称f(x)为“保等比数列函数”，下列函数是“保等比数列函数”的是（）.

A、 $f (x) = \frac{1}{| x |}$ B、f(x)=2x+1 C、 $f (x) = e ˣ$ D、f(x)=log₃|x|

查看试题解析
15. 《周髀算经》中“侧影探日行”一文有记载：“即取竹空，径一寸，长八尺，捕影而视之，空正掩目，而日应空之孔.”意为：“取竹空这一望筒，当望筒直径d是一寸，筒长t是八尺时(注：一尺等于十寸)，从筒中搜捕太阳的边缘观察，则筒的内孔正好覆盖太阳，而太阳的外缘恰好填满竹管的内孔.”如图所示，O为竹空底面圆心，则太阳角∠AOB的正切值为（）.

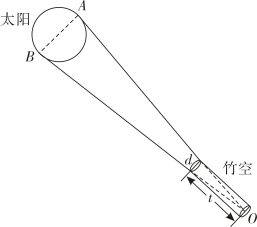A、 $\frac{1}{160}$ B、 $\frac{320}{160^{2} - 1}$ C、 $\frac{1}{80}$ D、 $\frac{160}{80} - 1$

查看试题解析
16. 已知F₁、F₂是椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点，Q是Γ上一动点，记 $∠ Q F_{1} F_{2} = θ_{1} ， ∠ Q F_{2} F_{1} = θ_{2} ，$ 若 $3 s i n θ_{1} (1 - c o s θ_{2}) = 2 s i n θ_{2} (1 + c o s θ_{1}) ，$ 则 $\frac{b}{a}$ 的值为（）.

A、 $\frac{2 \sqrt{6}}{5}$ B、 $\frac{\sqrt{6}}{5}$ C、 $\frac{4 \sqrt{3}}{7}$ D、 $\frac{2 \sqrt{3}}{7}$

查看试题解析

三、解答题(本题共5道题，满分78分)

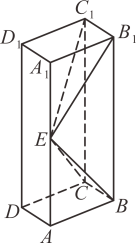
17. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面ABCD是正方形，点E在棱AA₁上，BE⊥EC₁.

(1)、证明：BE⊥平面EB₁C₁；

(2)、若AA₁=2，AB=1，求四棱锥 $E - B B_{1} C_{1} C$ 的体积.

查看试题解析
18. 已知数列 $\{x_{n}\}$ ，若对于任意正整数n， $x_{n} + x_{n + 2} - x_{n + 1}$ 仍为数列 $\{x_{n}\}$ 中的项，则称数列 $\{x_{n}\}$ 为“回归数列”.

(1)、已知 $a_{n} = 3 ⁿ (n \geq 1, n \in N) ，$ 判断数列 $\{a_{n}\}$ 是否为“回归数列”，并说明理由；

(2)、若数列 $\{b_{n}\}$ 为“回归数列”，且对于任意正整数n，均有 $b_{n} < b_{n + 1}$ 成立，证明：数列 $\{b_{n}\}$ 为等差数列.

查看试题解析
19. “我将来要当一名麦田里的守望者，有那么一群孩子在一大块麦田里玩，几千几万的小孩子，附近没有一个大人，我是说，除了我.”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块平面四边形ABCD的麦田里成为守望者.如图所示，为了分割麦田，他将B、D连接，经测量知AB=BC=CD=1，AD=2.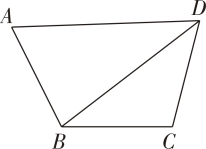

(1)、霍尔顿发现无论BD多长，2cosA-cosC都为一个定值.请你证明霍尔顿的结论，并求出这个定值；

(2)、霍尔顿发现小麦的生长和发育与分割土地面积的平方和呈正相关关系.记△ABD与 $△ C B D$ 的面积分别为S₁和S₂，为了更好地规划麦田，请你帮助霍尔顿求出 $S_{1}^{2} + S_{2}^{2}$ 的最大值.

查看试题解析
20. 已知椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $A (\sqrt{3}, \frac{\sqrt{13}}{2}) ，$ 且Γ的左焦点为 $F (- 2 \sqrt{3}, 0) ，$ 直线l与Γ交于M，N两点.

(1)、求椭圆Γ的方程；

(2)、若 $\vec{M P} = \frac{1}{2} \vec{P N} ，$ 且点P的坐标为(0，1)，求直线l的斜率；

(3)、若 $| \vec{O M} + \vec{O N} | = 4 ，$ 其中O为坐标原点，求△MON面积的最大值.

查看试题解析
21. 已知函数 $h (x) = l n x + \frac{λ}{x} ，$ 其中λ为实数.

(1)、若y=h(x)是定义域上的单调函数，求实数λ的取值范围；

(2)、若函数y=h(x)有两个不同的零点，求实数λ的取值范围；

(3)、记g(x)=h(x)-λx，若p，q(p<q)为g(x)的两个驻点，当λ在区间 $[\frac{4}{17}, \frac{2}{5}]$ 上变化时，求|g(p)-g(q)|的取值范围.

查看试题解析