北京市海淀区名校2023-2024学年高二上学期数学期中试卷
试卷更新日期:2023-11-27 类型:期中考试
一、选择题(本大题共8小题,每小题5分,共40分)
-
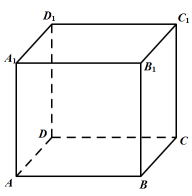
1. 如图,分别是长方体的棱的中点,则等于( )
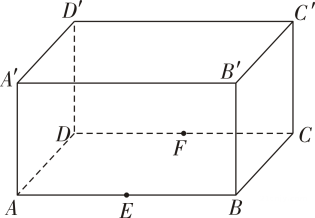 A、 B、 C、 D、2. 直线的倾斜角是( )A、 B、 C、 D、3. 若抛物线的焦点坐标为 , 则其准线方程为( )A、 B、 C、 D、4. 如图,已知四面体的所有棱长都等于分别是棱的中点.则与分别等于( )
A、 B、 C、 D、2. 直线的倾斜角是( )A、 B、 C、 D、3. 若抛物线的焦点坐标为 , 则其准线方程为( )A、 B、 C、 D、4. 如图,已知四面体的所有棱长都等于分别是棱的中点.则与分别等于( )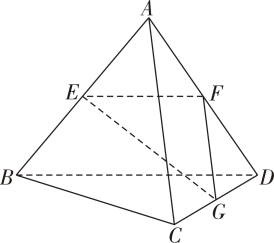 A、和 B、和 C、和 D、和5. 设椭圆的两个焦点为 , , 过点的直线交椭圆于A、B两点,如果 , 那么的值为( )A、2 B、10 C、12 D、146. 抛物线上的点到其焦点的距离的最小值为( )A、 B、1 C、2 D、47. 若双曲线的焦点到其渐近线的距离为 , 则双曲线的方程为( )A、 B、 C、 D、8. 如图,在正方体中,点为棱的中点,点为面内一点, , 则( )
A、和 B、和 C、和 D、和5. 设椭圆的两个焦点为 , , 过点的直线交椭圆于A、B两点,如果 , 那么的值为( )A、2 B、10 C、12 D、146. 抛物线上的点到其焦点的距离的最小值为( )A、 B、1 C、2 D、47. 若双曲线的焦点到其渐近线的距离为 , 则双曲线的方程为( )A、 B、 C、 D、8. 如图,在正方体中,点为棱的中点,点为面内一点, , 则( )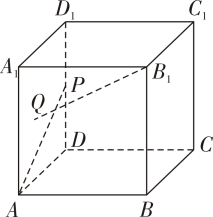 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题5分,共30分)
-
9. 若经过点的直线与直线垂直,则 .10. 已知平面的法向量为 , 平面的法向量为 , 若 , 则 .11. 已知两圆和相交,则圆与圆的公共弦所在直线的方程为 .12. 设分别是空间两直线的方向向量,则直线所成角的大小为 .13. 已知是直线上一点,且是直线的一个法向量,则直线的方程为 .14. 设点分别为椭圆的左、右焦点,点是椭圆上任意一点,若使得成立的点恰好是4个,则实数的一个取值可以为 .
三、解答题(本大题共3小题,共30分)
-
15. 已知的三个顶点 , 求经过两边和的中点的直线的方程.16. 已知直线与圆 .(1)、若直线与圆相切,求实数的值;(2)、当时,直线与圆交于点 , 设为原点,求的面积.17. 如图,四棱锥的底面是矩形,底面 , 为的中点.
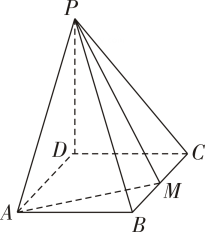 (1)、求证:平面;(2)、求平面与平面所成的角的余弦值.
(1)、求证:平面;(2)、求平面与平面所成的角的余弦值.四、填空题(本大题共4小题,每小题4分,共16分)
-
18. 在空间直角坐标系中,已知点 , 若四点共面,则 .19. 已知双曲线的右焦点为 , 过点作轴的垂线在第一象限与双曲线及其渐近线分别交于两点.若点是线段的中点,则双曲线的离心率为 .20. 如图,在长方体中, , , 点在侧面上.若点到直线和的距离相等,则的最小值是 .
 21. 在平面直角坐标系中,到两个点和的距离之积等于4的轨迹记作曲线 , 对于曲线及其上一点 , 有下列四个结论:
21. 在平面直角坐标系中,到两个点和的距离之积等于4的轨迹记作曲线 , 对于曲线及其上一点 , 有下列四个结论:①曲线关于轴对称;
②曲线上有且仅有一点 , 满足;
③曲线上所有的点的横坐标 , 纵坐标;
④的取值范围是 .
其中,所有正确结论的序号是 .
五、解答题(本大题共3小题,共34分)
-
22. 如图,直四棱柱中,底面是边长为1的正方形,点在棱上
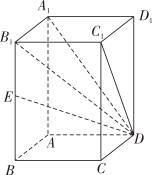 (1)、求证:;(2)、从条件①、条件②、条件③这三个条件中选择两个作为已知,使得平面 , 并给出证明.
(1)、求证:;(2)、从条件①、条件②、条件③这三个条件中选择两个作为已知,使得平面 , 并给出证明.条件①:为的中点;
条件②:平面;
条件③: .
(3)、若为的中点,且点到平面的距离为1,求的长度.23. 已知椭圆的左、右顶点分别为 , 上、下顶点分别为 , 四边形的周长为 .(1)、求椭圆的方程;(2)、设点为椭圆的左焦点,点 , 过点作的垂线交椭圆于点 , 连接与交于点 . 试判断是否为定值?若是,求出这个定值;若不是,说明理由.24. 个有次序的实数所组成的有序数组称为一个维向量,其中称为该向量的第个分量.特别地,对一个维向量 , 若 , 称为维信号向量.设 , 则和的内积定义为 , 且 .(1)、直接写出4个两两垂直的4维信号向量.(2)、证明:不存在14个两两垂直的14维信号向量.(3)、已知个两两垂直的2024维信号向量满足它们的前个分量都是相同的,求证: .