福建省福州市仓山区2023-2024学年高二上学期数学期中试卷

试卷更新日期：2023-11-27 类型：期中考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 直线 $x = 2023$ 的倾斜角为（）

A、0 B、 $\frac{π}{4}$ C、 $\frac{π}{2}$ D、不存在

查看试题解析
2. 方程 $x^{2} + y^{2} + 2 x - m = 0$ 表示一个圆，则 $m$ 的取值范围是（）

A、 $(- 1 ， + \infty)$ B、 $(- \infty ， - 1)$ C、 $[- 1 ， + \infty)$ D、 $(- \infty ， - 1]$

查看试题解析
3. 在正四面体 $P - A B C$ 中， $O$ 是 $△ A B C$ 的中心， $A B = 2$ ，则 $\vec{P O} \cdot (\vec{P A} + \vec{P B})$ 等于（）

A、 $\frac{10}{9}$ B、 $\frac{2 \sqrt{6}}{3}$ C、 $\frac{8 \sqrt{2}}{3}$ D、 $\frac{16}{3}$

查看试题解析
4. 在下列条件中，能使空间中的四点M ， A ， B ， C共面的是（）

A、 $\vec{O M} = 2 \vec{O A} - \vec{O B} - \vec{O C}$ B、 $\vec{O M} = \frac{1}{5} \vec{O A} + \frac{1}{3} \vec{O B} + \frac{1}{2} \vec{O C}$ C、 $\vec{M A} + 2 \vec{M B} + \vec{M C} = \vec{0}$ D、 $\vec{O M} + \vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$

查看试题解析
5. 《九章算术》是我国东汉初年编订的一部数学经典著作，其在卷第五《商功》中描述的几何体“阳马”实为“底面为矩形，一侧棱垂直于底面的四棱锥”．如图，在“阳马” $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ， $A D = 2 A B = P A$ ，则直线 $P C$ 与面 $P B D$ 所成角的正弦值为（）

A、 $\frac{\sqrt{6}}{9}$ B、 $\frac{\sqrt{75}}{9}$ CD． C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
6. 不论实数 $a$ 取何值时，直线 $(2 a - 1) x + (- a + 3) y - 3 = 0$ 都过定点 $M$ ，则直线 $2 x - y + 3 = 0$ 关于点 $M$ 的对称直线方程为（）

A、 $x - 2 y - 6 = 0$ B、 $x - 2 y = 0$ C、 $2 x - y - 9 = 0$ D、 $2 x - y - 3 = 0$

查看试题解析
7. 如图，在直四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B ⊥ A D$ ， $A B = A D = 1$ ， $A A_{1} > A B$ ， E ， F分别是侧棱 $B B_{1}$ ， $D D_{1}$ 上的动点，且平面 $A E F$ 与平面 $A B C$ 所成角的大小为 $30 °$ ，则线段 $B E$ 的长的最大值为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
8. 已知圆 $C ： x^{2} + y^{2} - 4 x - 4 y - 10 = 0$ ，直线 $l ： x - y + c = 0$ ，若圆 $C$ 上有四个不同的点到直线 $l$ 的距离为 $2 \sqrt{2}$ ，则 $c$ 的取值范围是（）

A、 $[- 2 \sqrt{2} ， 2 \sqrt{2}]$ B、 $(- 2 \sqrt{2} ， 2 \sqrt{2})$ C、 $[- 2 ， 2]$ D、 $(- 2 ， 2)$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

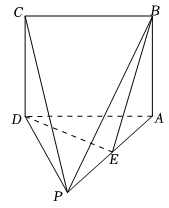
9. 在空间直角坐标系中，向量 $\vec{a} = (m ， 2 ， 2)$ ， $\vec{b} = (- 2 ， 1 ， 1)$ ，则下列结论正确的是（）

A、 $| \vec{b} | = \sqrt{6}$ B、若 $m = - 4$ ，则 $\vec{a} / / \vec{b}$ C、若 $m = 1$ ，则 $\vec{a} - \vec{b} = (- 3 ， - 1 ， - 1)$ D、若 $m = 2$ ，则 $\vec{a} ⊥ \vec{b}$

查看试题解析
10. 下列说法错误的是（）

A、“ $a = - 1$ ”是“直线 $a^{2} x - y + 1 = 0$ 与直线 $x - a y - 2 = 0$ 互相垂直”的充要条件 B、直线 $x s i n α + y + 2 = 0$ 的倾斜角 $θ$ 的取值范围是 $[0 ， \frac{π}{4}] ∪ [\frac{3 π}{4} ， π)$ C、过 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 两点的所有直线，其方程均可写为 $\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}}$ D、已知 $A (2 ， 4)$ ， $B (1 ， 1)$ ，若直线 $l$ ： $k x + y + k - 2 = 0$ 与线段 $A B$ 有公共点，则 $k \in [- \frac{1}{2} ， \frac{2}{3}]$

查看试题解析
11. 点 $P$ 是直线 $l$ ： $x + y = 3$ 上的一个动点，A ， B是圆 $O$ ： $x^{2} + y^{2} = 1$ 上的两个动点，则（）

A、点 $A$ 到直线 $l$ 的距离大于 $\frac{3}{2}$ B、点 $A$ 到直线 $l$ 的距离小于 $\frac{7}{2}$ C、存在点P ， A ， B ，使得 $∠ A P B = 90 °$ D、若直线PA ， PB均与圆 $O$ 相切，则直线AB过定点 $(\frac{1}{3} ， \frac{1}{3})$

查看试题解析
12. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是边长为1的正方形． $P D ⊥$ 底面 $A B C D$ ， $P D = \sqrt{3}$ ，点 $E$ 是棱PB上一点（不包括端点）．F是平面 $P C D$ 内一点，则（）

A、存在点 $E$ ，使 $A E / /$ 平面 $P C D$ B、存在点 $E$ ，使 $P B ⊥$ 平面 $A C E$ C、 $A E + E F$ 的最小值为 $\frac{4 \sqrt{5}}{5}$ D、以 $D$ 为球心，半径为1的球与四棱锥 $P - A B C D$ 的四个侧面的交线长为 $\frac{4 π}{3}$

查看试题解析

三、填空题：本题共6小题，每小题5分，共30分．

13. 若直线 $x - y + 1 = 0$ 与圆 $x^{2} + y^{2} - 2 x + 1 - a = 0$ 相切，则 $a =$ ．

查看试题解析
14. 已知点 $A (1 ， 0 ， 2)$ ， $B (- 1 ， 1 ， 2)$ ， $C (1 ， 1 ， - 2)$ ，则点 $A$ 到直线 $B C$ 的距离是．

查看试题解析
15. 在平面 $A B C D$ 中， $\vec{A B} = (- 1 ， 1 ， - 1)$ ， $\vec{A C} = (- 1 ， 3 ， 4)$ ， $\vec{A D} = (a ， - 2 ， 0)$ ，则实数 $a =$ ．

查看试题解析
16. 若直线 $a_{1} x + b_{1} y + 1 = 0$ 和直线 $a_{2} x + b_{2} y + 1 = 0$ 都过点 $A (4 ， 3)$ ，则过点 $P_{1} (a_{1} ， b_{1})$ 和点 $P_{2} (a_{2} ， b_{2})$ ，的直线方程为．

查看试题解析
17. 已知实数 $x ， y$ 满足 $x^{2} + y^{2} = 2 | x | + 2 | y |$ ，则 $\frac{y}{x - 4}$ 的最大值为.

查看试题解析
18. 关于 $x$ 的不等式 $| k x - \sqrt{4 - x^{2}} - 3 | \leq 3 \sqrt{k^{2} + 1}$ 恒成立，则 $k$ 的取值范围是．

查看试题解析

四、解答题：本题共5小题，共60分．

19. 已知直线 $l_{1}$ 的方程为 $y = - 2 x + 3$ ．

(1)、若直线 $l_{2}$ 与 $l_{1}$ 平行，且过点 $(- 1 ， 3)$ ，求直线 $l_{2}$ 的方程；

(2)、若直线 $l_{2}$ 与 $l_{1}$ 垂直，且 $l_{2}$ 与两坐标轴围成的三角形面积为4，求直线 $l_{2}$ 的方程．

查看试题解析
20. 如图，在三棱台 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ B A C = 90 °$ ， $A B = A C = 4$ ， $A_{1} A = A_{1} B_{1} = 2$ ，侧棱 $A_{1} A ⊥$ 平面 $A B C$ ，点 $D$ 是棱 $C C_{1}$ 的中点．

(1)、证明： $B B_{1} ⊥$ 平面 $A B_{1} C$ ；

(2)、求点 $B_{1}$ 到平面 $A B D$ 的距离；

(3)、 $B C D$ 与平面 $A B D$ 的夹角的余弦值．

查看试题解析
21. 在平面直角坐标系xOy中，已知圆C： $x^{2} + y^{2} - 4 x - 8 y + 12 = 0$ ，圆N过原点O及点 $A (- 2 ， 0)$ 且与圆C外切．

(1)、求圆N的标准方程；

(2)、若过点A的直线l被两圆截得的弦长相等，求直线l的方程．

查看试题解析
22. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ，正方形 $A B C D$ 的边长为2，E是PA的中点．

(1)、 $P C / /$ 平面BDE；

(2)、若 $P A = 2$ ，线段PC上是否存在一点 $F$ ，使 $A F ⊥$ 平面BDE？若存在，求出PF的长度；若不存在，请说明理由．

查看试题解析
23. 在平面直角坐标系xOy中，已知 $A (- 1 ， - 1)$ ， $B (2 ， - 1)$ ，以原点O为圆心的圆与直线AB相切．

(1)、求圆O的方程；

(2)、若直线l： $2 x + y + c = 0$ 与圆O相交于M ， N两点，且 $O M ⊥ O N$ ，求c的值；

(3)、在直线AO上是否存在异于A的定点Q ，使得对圆O上任意一点P ，都有 $\frac{| P A |}{| P Q |} = λ$ （ $λ$ 为常数）？若存在，求出点Q的坐标及 $λ$ 的值；若不存在，请说明理由．

查看试题解析