2023年浙教版数学七年级上册第六章 图形的初步知识 单元测试(B卷)
试卷更新日期:2023-11-26 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 用一个平面去截一个正方体,则截面的形状不可能为( )A、等腰三角形 B、梯形 C、正七边形 D、五边形2. 如果线段 , , 那么下面说法中正确的是( )A、M点在线段上 B、M点在直线上 C、M点在直线外 D、M点可能在直线上,也可能在直线外3. 把弯曲的道路改直就能缩短路程,下列数学语言解释正确的是( )A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、对顶角相等4. 已知A,B,C是同一直线上的三个点,且AB=9cm,BC=4cm,D是BC的中点,则AD的长是( )A、13cm B、7cm C、11cm D、7cm或11cm5. 如图,是直线,是直线上一点,、是两条射线,则图中小于平角的角有( )
 A、3个 B、4个 C、5个 D、6个6.
A、3个 B、4个 C、5个 D、6个6.如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )
 A、∠BAC>∠CAD B、∠DAE>∠CAD C、∠CAE<∠BAC+∠DAE D、∠BAC<∠DAE7. 如图, 将三个三角板直角顶点重叠在一起, 公共的直角顶点为点 , 若 , , 那么 的度数为( )
A、∠BAC>∠CAD B、∠DAE>∠CAD C、∠CAE<∠BAC+∠DAE D、∠BAC<∠DAE7. 如图, 将三个三角板直角顶点重叠在一起, 公共的直角顶点为点 , 若 , , 那么 的度数为( ) A、 B、 C、 D、8. 下列四个图中,能表示线段的是( )A、
A、 B、 C、 D、8. 下列四个图中,能表示线段的是( )A、 B、
B、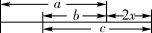 C、
C、 D、
D、 9. 下列说法中,正确的是( )A、相等的角是对顶角 B、若AB=BC,则点B是线段AC的中点 C、在同一平面内,过一点有且仅有一条直线垂直于已知直线 D、一个锐角的补角大于等于该锐角的余角10. 已知 与 满足 ,下列式子表示的角:① :② ;③ ;④ 中,其中是 的余角的是( )A、①② B、①③ C、②④ D、③④
9. 下列说法中,正确的是( )A、相等的角是对顶角 B、若AB=BC,则点B是线段AC的中点 C、在同一平面内,过一点有且仅有一条直线垂直于已知直线 D、一个锐角的补角大于等于该锐角的余角10. 已知 与 满足 ,下列式子表示的角:① :② ;③ ;④ 中,其中是 的余角的是( )A、①② B、①③ C、②④ D、③④二、填空题(每题4分,共24分)
-
11. 钟表上的时针转动一周形成一个圆面,这说明了 .12. 如图,小亮将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,请你用数学知识解释他这样操作的原因是
 13. 下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 地到 地架设电线,总是尽可能沿着线段 架设.其中能用“两点之间,线段最短”来解释的现象有.(填序号)14. 已知线段AB=12,C是线段AB上一点,且BC=2,点D在射线AB上,若DA=4DC,则BD的长为.15. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 .
13. 下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 地到 地架设电线,总是尽可能沿着线段 架设.其中能用“两点之间,线段最短”来解释的现象有.(填序号)14. 已知线段AB=12,C是线段AB上一点,且BC=2,点D在射线AB上,若DA=4DC,则BD的长为.15. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 . 16. 如图,将两块直角三角尺的直角顶点C叠放在一起.若 , 则∠ACB的度数为 .
16. 如图,将两块直角三角尺的直角顶点C叠放在一起.若 , 则∠ACB的度数为 .
三、解答题(共9题,共66分)
-
17. 如图,在平面内有三点.
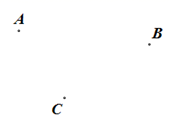 (1)、画直线;画射线;画线段;(2)、在线段上任取一点(不同于),连接 , 并延长至点 , 使;(3)、数一数,此时图中共有多少条线段?多少条射线?18. 如图,点P是线段AB上任一点,AB=12cm,C,D两点分别从点P,B同时向点A运动,且点C的运动速度为2cm/s,点D的运动速度为3cm/s,运动的时间为t s.
(1)、画直线;画射线;画线段;(2)、在线段上任取一点(不同于),连接 , 并延长至点 , 使;(3)、数一数,此时图中共有多少条线段?多少条射线?18. 如图,点P是线段AB上任一点,AB=12cm,C,D两点分别从点P,B同时向点A运动,且点C的运动速度为2cm/s,点D的运动速度为3cm/s,运动的时间为t s. (1)、若AP=8cm,
(1)、若AP=8cm,①运动1s后,求CD的长;②当点D在线段PB上运动时,试说明AC=2CD;
(2)、如果t=2s时,CD=1cm,试探索AP的值.19. 如图,直线AB、CD相交于点O,OM⊥AB.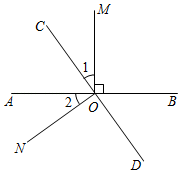 (1)、若∠1=∠2,证明:ON⊥CD;(2)、若∠1=∠BOC,求∠BOD的度数.20. 如图是小明用七巧板拼出的图案.
(1)、若∠1=∠2,证明:ON⊥CD;(2)、若∠1=∠BOC,求∠BOD的度数.20. 如图是小明用七巧板拼出的图案. (1)、请赋予该图形一个积极的含义;(2)、请你找出图中二组平行线段和二对互相垂直的线段,用符号表示他们;(3)、找出图中一个锐角,一个钝角,一个直角,将它们表示出来,并指出它们的度数.21. 定义:在一个已知角内部,一条线分已知角成两个新角,其中一个角度数为另个角度数的两倍,我们把这条线叫做这个已知角的三等分线.(1)、如图,已知∠AOB=120°,若OC是∠AOB三等分线,求∠AOC的度数.
(1)、请赋予该图形一个积极的含义;(2)、请你找出图中二组平行线段和二对互相垂直的线段,用符号表示他们;(3)、找出图中一个锐角,一个钝角,一个直角,将它们表示出来,并指出它们的度数.21. 定义:在一个已知角内部,一条线分已知角成两个新角,其中一个角度数为另个角度数的两倍,我们把这条线叫做这个已知角的三等分线.(1)、如图,已知∠AOB=120°,若OC是∠AOB三等分线,求∠AOC的度数. (2)、点O在线段AB上(不含端点A,B),在直线AB同侧作射线OC,OD.设∠AOC=3t,∠BOD=5t.
(2)、点O在线段AB上(不含端点A,B),在直线AB同侧作射线OC,OD.设∠AOC=3t,∠BOD=5t.①当OC是∠AOD的三等分线时,求t的值.
②当OC是∠BOD的三等分线时,求∠BOD的度数.
22. 定义:从一个角的顶点引出的一条射线,把这个角分成1:2两部分,这条射线叫做这个角的内倍分线. (1)、如图1,OM是∠AOB的一条内倍分线,满足∠BOM=2∠AOM,若∠AOB =45°,求∠AOM的度数.(2)、已知∠AOB=60°,把一块含有60角的三角板COD按如图2叠放.将三角板COD绕顶点O以2度/秒的速度按顺时针方向旋转秒(0<t<180) 。
(1)、如图1,OM是∠AOB的一条内倍分线,满足∠BOM=2∠AOM,若∠AOB =45°,求∠AOM的度数.(2)、已知∠AOB=60°,把一块含有60角的三角板COD按如图2叠放.将三角板COD绕顶点O以2度/秒的速度按顺时针方向旋转秒(0<t<180) 。①t为何值时,射线OC是∠AOD的内倍分线;
②在三角板COD转动的同时,射线OB以每秒n(0<n<1)度的速度绕O点逆时针方向旋转至OB',在旋转过程中存在OB'恰好同时是∠AOD,∠AOC的内倍分线,请直接写出n的值.
23. 将直角三角板OMN的直角顶点О放在直线AB上,射线OC平分∠AON.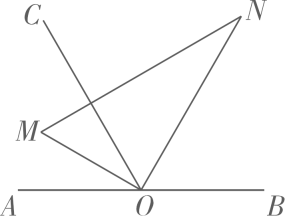 (1)、如图,若∠BON=60°,求∠COM的度数;(2)、将直角三角板OMN绕顶点О按逆时针方向旋转,在旋转过程中:
(1)、如图,若∠BON=60°,求∠COM的度数;(2)、将直角三角板OMN绕顶点О按逆时针方向旋转,在旋转过程中:①当∠BON=140°时,求∠COM的度数:
②直接写出∠BON和∠COM之间的数量关系.
24. 如图,直线 , 相交于点 , 平分 . (1)、【基础尝试】
(1)、【基础尝试】
如图1,若 ,求 的度数;(2)、【画图探究】
作射线 ,设 ,请你利用图2画出图形,探究 与 之间的关系,结果用含 的代数式表示 .(3)、【拓展运用】
在第(2)题中, 可能和 互补吗?请你作出判断并说明理由.25. 问题提出:如图1,A、B、C、D表示四个村庄, 村民们准备合打一口水井.
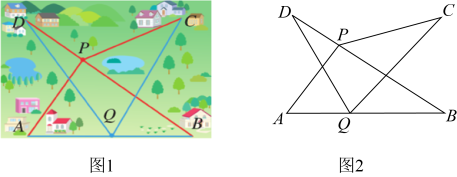 (1)、问题解决:
(1)、问题解决:若水井的位置现有P、Q两种选择方案.点P在线段上,点Q在线段上,哪一种方案的水井到各村庄的距离总和较小?请说明你判断的理由.
(2)、你能给出一种使水井到各村庄的距离之和最小的方案吗?若能,请图2中标出水井的位置点M,并说明理由.(3)、问题拓展:如果(2)问中找出的水井经过招标,由两个工程队修建(不存在同时修建). 已知甲工程队单独完成需要80天,乙工程队单独完成需要120天,且甲工程队比乙工程队每天多修建.
问水井要修建几米?(4)、若甲工程队每天的施工费为0.5万元,乙工程队每天的费用是0.25万元,为了缩短工期和节约资金,则甲工程队最多施工几天才能使工程款不超过35万元?(甲、乙两队的施工时间不足一天按一天算).