2023年浙教版数学七年级上册第六章 图形的初步知识 单元测试(A卷)
试卷更新日期:2023-11-26 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下面的四个几何图形中,表示平面图形的是( )A、
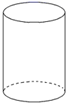 B、
B、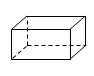 C、
C、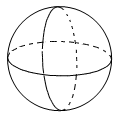 D、
D、 2. 图中是将一平面图形绕直线l旋转一周得到的,则该平面图形是( )
2. 图中是将一平面图形绕直线l旋转一周得到的,则该平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
3. 在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( ) A、1个 B、2个 C、3个 D、4个4. 如图,用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A、1个 B、2个 C、3个 D、4个4. 如图,用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( ) A、垂线段最短 B、经过一点有无数条直线 C、线段可以向两个方向延长 D、两点之间,线段最短5. 如图,已知线段AB=10cm,线段CB=3 cm,则线段AC的长是( )
A、垂线段最短 B、经过一点有无数条直线 C、线段可以向两个方向延长 D、两点之间,线段最短5. 如图,已知线段AB=10cm,线段CB=3 cm,则线段AC的长是( ) A、7 cm B、6cm C、5cm D、4cm6. 下列说法正确的是( )A、非负数就是指一切正数 B、数轴上任意一点都对应一个实数 C、两个锐角的和一定大于直角 D、一条直线就是一个平角7. 若 , , ,则有( )A、 B、 C、 D、8. 一副三角板如图摆放,则的度数是( )
A、7 cm B、6cm C、5cm D、4cm6. 下列说法正确的是( )A、非负数就是指一切正数 B、数轴上任意一点都对应一个实数 C、两个锐角的和一定大于直角 D、一条直线就是一个平角7. 若 , , ,则有( )A、 B、 C、 D、8. 一副三角板如图摆放,则的度数是( ) A、90° B、75° C、60° D、15°9. 已知一个角的余角等于40°,则这个角的补角等于( )A、130° B、140° C、150° D、160°10. 如图,已知直线AB和CD相交于点O,于点O,图中∠1与∠2的关系是( )
A、90° B、75° C、60° D、15°9. 已知一个角的余角等于40°,则这个角的补角等于( )A、130° B、140° C、150° D、160°10. 如图,已知直线AB和CD相交于点O,于点O,图中∠1与∠2的关系是( ) A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定二、填空题(每题4分,共24分)
-
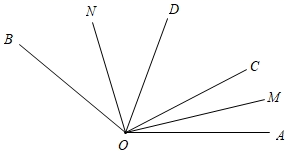
11. 如图,以O为端点的射线有条,图中线段有条.
 12. 如图,线段 BD =AB=CD, 点 M、N分别是线段AB、CD的中点,且MN = 20cm, 则 AC的长为 .
12. 如图,线段 BD =AB=CD, 点 M、N分别是线段AB、CD的中点,且MN = 20cm, 则 AC的长为 .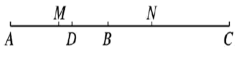 13. 把2.36°表示成度分、秒的形式为 .14. 比较图中、的大小:因为和是公共边,在的内部,所以 . (填“>”,“<”或“=”)
13. 把2.36°表示成度分、秒的形式为 .14. 比较图中、的大小:因为和是公共边,在的内部,所以 . (填“>”,“<”或“=”) 15. 若 , , 则 .16. 一个角的余角比它的补角的多12°,则这个角为.
15. 若 , , 则 .16. 一个角的余角比它的补角的多12°,则这个角为.三、解答题(共8题,共66分)
-
17. 计算:(1)、48°39′+67°31′(2)、180°﹣21°17′×518. 已知长方形的长为4 cm.宽为3 cm,将其绕它的一边所在的直线旋转一周,得到一个几何体.(1)、求此几何体的体积;(2)、求此几何体的表面积.(结果保留π)
19. 如图,已知平面上三点 , , , 按下列要求画图,并回答问题: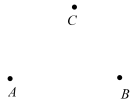 (1)、画射线 , 线段;(2)、连接 , 并在的延长线上取一点 , 使得;(3)、画直线;(4)、通过测量可得,点到直线的距离是 . (精确到)20. 如图,已知直线 , 射线 , 线段.
(1)、画射线 , 线段;(2)、连接 , 并在的延长线上取一点 , 使得;(3)、画直线;(4)、通过测量可得,点到直线的距离是 . (精确到)20. 如图,已知直线 , 射线 , 线段. (1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.21. 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)、用无刻度的直尺和圆规作图:延长到点D,使 , 连接.(2)、比较与的大小,并说明理由.21. 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE. (1)、求∠DOF的度数.(2)、若 , 求∠EOF的度数.22. 已知点B在线段AC上,点D在线段AB上.
(1)、求∠DOF的度数.(2)、若 , 求∠EOF的度数.22. 已知点B在线段AC上,点D在线段AB上. (1)、如图1,若AB=10 cm,BC=6 cm,D为线段AC的中点,求线段DB的长度.(2)、如图2,若BD= AB= CD,E为线段AB的中点,EC=16 cm,求线段AC的长度.
(1)、如图1,若AB=10 cm,BC=6 cm,D为线段AC的中点,求线段DB的长度.(2)、如图2,若BD= AB= CD,E为线段AB的中点,EC=16 cm,求线段AC的长度.