2023年浙教版数学七年级上册6.9直线的相交同步测试（培优版）

试卷更新日期：2023-11-26 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，点A是直线l外一点，过点A作 $A B ⊥ l$ 于点B．在直线l上取一点C，连接 $A C$ ，使 $A C = \frac{5}{3} A B$ ，点P在线段 $B C$ 上，连接 $A P$ ，若 $A B = 3$ ，则线段 $A P$ 的长不可能是（）

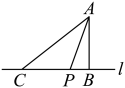A、3.5 B、4.1 C、5 D、5.5

查看试题解析
2. 如图， $O A ⊥ O C ， O B ⊥ O D$ ，4位同学观察图形后各自观点如下．甲： $∠ A O B = ∠ C O D$ ；乙： $∠ B O C + ∠ A O D = 180 °$ ；丙： $∠ A O B + ∠ C O D = 90 °$ ；丁：图中小于平角的角有6个；其中正确的结论是（）

A、甲、乙、丙 B、甲、乙、丁 C、乙、丙、丁 D、甲、丙、丁

查看试题解析
3. 如图，直线AB、CD相交于点O，，OF平分∠AOE，∠1=15°30′，则下列结论中，错误的是（）

A、∠2=45° B、∠1=∠3 C、∠AOD与∠1互为补角 D、∠1的余角等于75°30′

查看试题解析
4. 如果同一平面内有三条直线，那么它们交点个数是（）个.

A、3个 B、1或3个 C、1或2或3个 D、0或1或2或3个

查看试题解析
5. 如图，已知点A是射线BE上一点，过A作AC⊥BF，垂足为C，CD⊥BE，垂足为D.给出下列结论：①∠1是∠ACD的余角；②图中互余的角共有3对；③∠1的补角只有∠DCF；④与∠ADC互补的角共有3个.其中正确结论有（）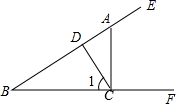

A、① B、①②③ C、①④ D、②③④

查看试题解析
6. 下列结论：①平面内3条直线两两相交，共有3个交点；②在平面内，若∠AOB =40°，∠AOC= ∠BOC，则∠AOC的度数为20°；③若线段AB=3， BC=2，则线段AC的长为1或5；④若∠a+∠β=180°，且∠a<∠β，则∠a的余角为 $\frac{1}{2}$ (∠β-∠a).其中正确结论的个数（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 下列说法：①若|a|＝﹣b，|b|＝b，则a＝b＝0；②若﹣a不是正数，则a为非负数；③|﹣a²|＝（﹣a）²；④若 $\frac{a}{| a |} + \frac{b}{| b |} = 0$ ，则 $\frac{a b}{| a b |} = - 1$ ；⑤平面内n条直线两两相交，最多 $\frac{n (n + 1)}{2}$ 个交点.其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，…那么六条直线最多有（）

A、21个交点 B、18个交点 C、15个交点 D、10个交点

查看试题解析
9. 平面内两两相交的7条直线，其交点个数最少是m个，最多是n个，则m+n的值为（　　）

A、18 B、20 C、22 D、24

查看试题解析
10. 若四条直线在平面内交点的个数为 $a$ ，则 $a$ 的可能取值有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题（每题4分，共24分）

11. 在直线AB上任取一点O，过点O作射线OC，OD，使OC⊥OD．当∠AOC= 30°时，∠BOD=

查看试题解析
12. 如图，将一副三角尺按不同的位置摆放，∠α与∠β一定相等的图形有(填序号)

查看试题解析
13. 如图，直线AB和CD相交于O ， OA平分∠COE ， ∠COE∶∠BOE＝2∶5，则∠EOD的度数为．

查看试题解析
14. 在 $∠ A O B$ 中，C，D分别为边 $O A$ ， $O B$ 上的点（不与顶点O重合）.对于任意锐角 $∠ A O B$ ，下面三个结论：
①点C和点D有无数个；

②连接 $C D$ ，存在 $∠ O D C$ 是直角；

③点C到边 $O B$ 的距离不超过线段 $C D$ 的长.

所有正确结论的序号是.

查看试题解析
15. 如图，点 $A$ 在直线 $m$ 上，点 $B$ 在直线 $l$ 上，点 $A$ 到直线 $l$ 的距离为 $a$ ，点 $B$ 到直线 $m$ 的距离为 $b$ ，线段 $A B$ 的长度为 $c$ ，通过测量等方法可以判断在 $a$ ， $b$ ， $c$ 三个数据中，最大的是．

查看试题解析
16. 如图，在 $4 \times 6$ 的正方形网格中，点 $A 、 B 、 C 、 D 、 E 、 F$ 都在格点上，连接 $C 、 D 、 E 、 F$ 中任意两点得到的所有线段中，与线段 $A B$ 垂直的线段是.

查看试题解析

三、解答题（共8题，共66分）

17. 如图，已知直线l表示一段公路，点A表示学校，点B表示书店，点C表示图书馆.

⑴请画出学校A到书店B的最短路线.
⑵在公路l上找一个路口M，使得 $A M + C M$ 的值最小.
⑶现要从学校A向公路l修一条小路，怎样修路才能使小路的长最短？请画出小路的路线，并用所学知识描述小路的方向.

查看试题解析
18. 如图， $A ， B ， C$ 是平面内三点.

(1)、按要求作图：请先用铅笔作图，确认无误后，再用黑色水笔描深.
①作射线 $B C$ ，过点 $B$ 作直线 $l$ ，使 $A ， C$ 两点在直线 $l$ 两旁；

②过点 $A$ 作直线 $l$ 的垂线段，垂足为 $E$ ；

③点 $P$ 为直线 $l$ 上任意一点，点 $Q$ 为射线 $B C$ 上任意一点，连结线段 $A P ， P Q$ .

(2)、在（1）所作图形中，若点 $A$ 到直线 $l$ 的距离为2，点 $A$ 到射线 $B C$ 的距离为5，点 $A$ 、 $B$ 之间的距离为8，点 $A ， C$ 之间的距离为6，则 $A P + P Q$ 的最小值为，依据是.

查看试题解析
19. 如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，

(1)、当∠BOC＝50°，∠DOE＝；当∠BOC＝70°，∠DOE＝；

(2)、通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由.

查看试题解析
20. 如图，直线AB和CD交于点O，射线OE平分∠AOD．

(1)、若∠BOD=50°，求∠COE的度数；

(2)、若射线OF⊥AB于点O，∠BOD=α°，请补全图形，并求∠EOF的度数

查看试题解析
21. 已知：直线AB与直线CD交于点O，过点O作 $O E ⊥ C D$ ．

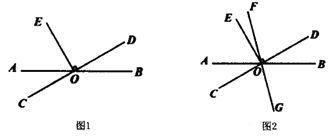(1)、如图1，若 $∠ A O E = 2 ∠ A O C$ ，求 $∠ B O E$ 的度数；

(2)、如图2，过点O画直线FG满足射线OF在 $∠ E O D$ 内部，且使 $∠ A O C = 2 ∠ E O F$ ，在不添加任何辅助线的情况下，请直接写出与 $∠ E O F$ 互余的角．

查看试题解析
22. 已知∠AOB=160°，∠COE是直角，OF平分∠AOE.

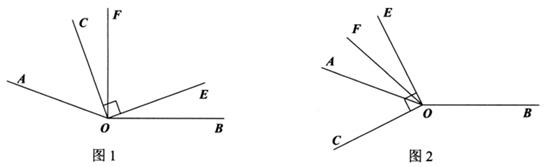(1)、如图1，若∠COF=32°，则∠BOE=；

(2)、如图1，若∠COF=m°，则∠BOE=；∠BOE与∠COF的数量关系为.

(3)、在已知条件不变的前提下，当∠COE绕点О逆时针转动到如图2的位置时，第（2）问中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.

查看试题解析
23. 已知，如图，点 $M$ 、 $N$ 分别代表两个村庄，直线 $l$ 代表两个村庄之间的一条燃气管道，根据村民燃气需求，计划在管道 $l$ 上某处修建一座燃气管理站，向两村庄接入管道．

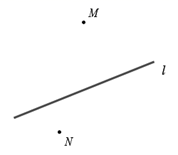(1)、若计划建一个离村庄 $M$ 最近的燃气管理站，请画出燃气管理站的位置（用点 $P$ 表示），并写出这样做的依据．

(2)、若考虑到管道铺设费用问题，希望燃气管理站的位置到村庄 $M$ 、村庄 $N$ 距离之和最小，画出燃气管理站的位置（用点 $Q$ 表示），并写出这样做的依据．

查看试题解析
24. 如图（1），点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，将一直角的直角顶点放在点 $O$ 处，即 $∠ M O N ，$ 反向延长射线 $O N$ ，得到射线 $O D$ .

(1)、当 $∠ M O N$ 的位置如图（1）所示时，使 $∠ N O B = 20^{\circ}$ ，若 $∠ B O C = 120^{\circ}$ ，求 $∠ C O D$ 的度数.

(2)、当 $∠ M O N$ 的位置如图（2）所示时，使一边 $O M$ 在 $∠ B O C$ 的内部，且恰好平分 $∠ B O C$ ，
问：射线 $O N$ 的反向延长线 $O D$ 是否平分 $∠ A O C ?$ 请说明理由：注意：不能用问题（1）中的条件

(3)、当 $∠ M O N$ 的位置如图 $(3)$ 所示时，射线 $O N$ 在 $∠ A O C$ 的内部，若 $∠ B O C = 120^{\circ}$ .试探究 $∠ A O M$ 与 $∠ N O C$ 之间的数量关系，不需要证明，写出结论.

查看试题解析

2023年浙教版数学七年级上册6.9直线的相交 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学七年级上册6.9直线的相交同步测试（培优版）