（人教版）2024年中考数学一轮复习图形的变化--平移、旋转变换练习题

试卷更新日期：2023-11-26 类型：一轮复习

进入出卷网下载

一、选择题

1. 如图， $△ A B C$ 沿 $B C$ 方向平移后得到 $△ D E F$ ，已知 $B C = 7$ ， $E C = 2$ ，则平移的距离是（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

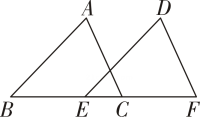查看试题解析
2. 随着人们生活水平的提高，对环境的保护越来越重视，下列垃圾分类标识的图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ，将 $△ A B C$ 绕点 $B$ 顺时针旋转得到 $△ D B E$ ，点 $A$ ， $C$ 的对应点分别为 $D$ ， $E .$ 当 $E D$ 的延长线经过点 $C$ 时，则下列结论一定正确的是（）

A、 $∠ A C B = ∠ D B E$ B、 $A C = B D$ C、 $∠ C B D = ∠ E B D$ D、 $C E = B E$

查看试题解析
4. 已知点 $A (2 ， m)$ 与点 $B (n ， - 5)$ 关于原点对称，则 $m + n$ 为（）

A、 $- 3$ B、3 C、7 D、 $- 7$

查看试题解析
5. 如图，在 $△ A B C$ 中，点 $A (- 2 ， - 1)$ ， $B (- 4 ， - 3)$ ，将 $△ A B C$ 先向右平移3个单位长度，再向上平移2个单位长度，则点 $B$ 的对应点 $B^{'}$ 的坐标为（）

A、 $(- 7 ， - 1)$ B、 $(- 1 ， - 1)$ C、 $(1 ， 1)$ D、 $(2 ， - 2)$

查看试题解析
6. 把图中的图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（）

A、 $60 °$ B、 $90 °$ C、 $120 °$ D、 $180 °$

查看试题解析
7. 点 $(5 ， 7)$ 关于原点对称的点为（）

A、 $(5 ， 7)$ B、 $(- 5 ， 7)$ C、 $(- 5 ， - 7)$ D、 $(5 ， - 7)$

查看试题解析
8. 若点 $A (a ， - 2)$ ， $B (3 ， b)$ 关于原点成中心对称，则a，b的值分别为（）

A、 $a = 3$ ， $b = - 2$ B、 $a = - 3$ ， $b = - 2$ C、 $a = 3$ ， $b = 2$ D、 $a = - 3$ ， $b = 2$

查看试题解析
9. 将一个正六边形绕其中心旋转后仍与原图形重合，旋转角的大小不可能是（）

A、60° B、90° C、180° D、360°

查看试题解析
10. 如图，将直角三角板ABC绕顶点A顺时针旋转到△AB'C'，点B’恰好落在CA的延长线上，∠B=30°，∠C=90°，则∠BAC'为（）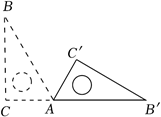

A、90° B、60° C、45° D、30°

查看试题解析

二、填空题

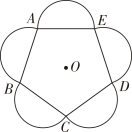
11. 在平面直角坐标系中，若点 $P (2 ， - 1)$ 与点 $Q (- 2 ， m)$ 关于原点对称，则 $m$ 的值是．

查看试题解析
12. 已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b =.

查看试题解析
13. 将直线 $y = - 6 x$ 向下平移2个单位长度，平移后直线的解析式为．

查看试题解析
14. 点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）.这个图案绕点O至少旋转°后能与原来的图案互相重合.

查看试题解析
15. 如图，将△ABC沿BC方向平移至△DEF处．若EC＝2BE＝2，则CF的长为．

查看试题解析

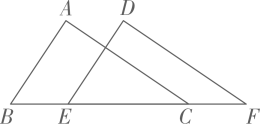
三、解答题

16. 如图，点E，F分别在正方形ABCD的边BC，CD上，且 $∠ E A F = 45 °$ ．把 $△ A D F$ 绕点A顺时针旋转 $90 °$ 得到 $△ A B G$ ．求证： $△ A G E ≌ △ A F E$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ，将 $△ A B C$ 绕点B逆时针旋转 $60 °$ 到 $△ D B E ， D E$ 的延长线与 $A C$ 相交于点F，连接 $D A 、 B F$ ，求证： $D A ∥ B C$ .

查看试题解析
18. 如图，在 $▱ A B C D$ 中，点E，F分别在边 $A D$ ， $B C$ 上，且 $A E = C F$ ，连接 $A F$ ， $C E$ ，求证：四边形 $A E C F$ 是中心对称图形.

查看试题解析
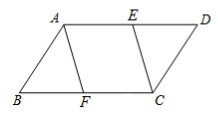19. 如图所示，点P是正方形ABCD内的一点，连接AP，BP，CP，将△PAB绕着点B顺时针旋转90°到△P′CB的位置.若AP=2，BP=4，∠APB=135°，求PP′及PC的长.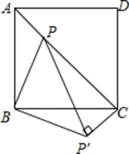

查看试题解析

四、综合题

20. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点的坐标分别为 $A (- 4 ， 3) ， B (- 3 ， 1) ， C (- 1 ， 3)$ ，请按下列要求画图：

(1)、将 $Δ A B C$ 先向右平移4个单位长度、再向下平移5个单位长度，得到 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标；

(2)、以点A为位似中心将 $Δ A B C$ 放大2倍，得到 $Δ A_{2} B_{2} C_{2}$ ，画出 $Δ A_{2} B_{2} C_{2}$ 并写出点B₂的坐标．

查看试题解析
21. 在 $△ A B C$ 中、 $∠ B = ∠ C = α (0 ° < α < 45 °)$ ， $A M ⊥ B C$ 于点M，D是线段 $M C$ 上的动点（不与点M，C重合），将线段 $D M$ 绕点D顺时针旋转 $2 α$ 得到线段 $D E$ ．

(1)、如图1，当点E在线段 $A C$ 上时，求证：D是 $M C$ 的中点；

(2)、如图2，若在线段 $B M$ 上存在点F（不与点B，M重合）满足 $D F = D C$ ，连接 $A E$ ， $E F$ ，直接写出 $∠ A E F$ 的大小，并证明．

查看试题解析
22. 如图1，一大一小两个等腰直角三角形叠放在一起， $M$ ， $N$ 分别是斜边 $D E$ ， $A B$ 的中点， $D E = 2 ， A B = 4$ ．

(1)、将 $△ C D E$ 绕顶点 $C$ 旋转一周，请直接写出点 $M$ ， $N$ 距离的最大值和最小值；

(2)、将 $△ C D E$ 绕顶点 $C$ 逆时针旋转 $120 °$ （如图 $2$ ），求 $M N$ 的长．

查看试题解析
23. 图形变换中的数学，问题情境：在课堂上，兴趣学习小组对一道数学问题进行了深入探究，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点D是AB的中点，连接CD．
探索发现：

(1)、如图①，BC与BD的数量关系是；

(2)、如图①，CD与AB的数量关系是 ▲ ；并说明理由．

(3)、如图②，若P是线段CB上一动点（点P不与点B，C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想BF，BP，BD三者之间的数量关系，并证明你的结论；

(4)、若点P是线段CB延长线上一动点，按照（3）中的作法，请在图③中补全图象，并直接写出BF、BP、BD三者之间的数量关系．

查看试题解析

（人教版）2024年中考数学一轮复习 图形的变化--平移、旋转变换 练习题

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2024年中考数学一轮复习图形的变化--平移、旋转变换练习题