2023年浙教版数学七年级上册6.9直线的相交 同步测试（基础版）
试卷更新日期：2023-11-26 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 下列各图形中，有对顶角的是（ ）A、
B、
C、
D、
2. 如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（ ）
A、1条 B、2条 C、3条 D、4条3. 下列选项中，∠1和∠2是对顶角的是（ ）A、
B、
C、
D、
4. 如图，利用工具测量角，则∠1的大小（ ）
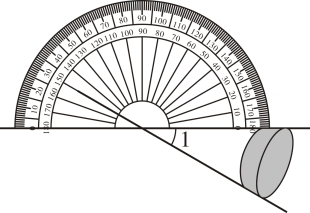A、30° B、60° C、120° D、150°5. 在下列图形中，线段的长表示点P到直线的距离的是（ ）A、
B、
C、
D、
6. 如图，直线AB，CD相交于点O，∠2=3∠1，∠BOD=108°，则∠1=（ ）
A、27° B、36° C、81° D、72°7. 如图，直线相交于点O， ， 若 ， 则的度数为（ ）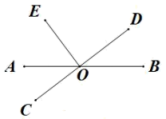
A、 B、 C、 D、8. 如图，已知直线、相交于点O，平分 ， 若 ， 则度数是（ ）
A、65° B、50° C、25° D、130°9. 如图，点P是直线l外一点，从点P向直线l引PA，PB，PC，PD（点A，B，C，D在直线l上）4条线段，其中于点C．这4条线段中，长度最短的是（ ）
A、PA B、PB C、PC D、PD10. 如图，点P在直线外， ， ， 则线段的值可能为（ ）
A、1 B、2 C、3 D、4二、填空题（每题4分，共24分）
-
11. 如图，口渴的牛儿在A点处想尽快地到达小河边喝水，它应该沿着线路AB奔跑，其中蕴含的数学依据是.
12. 如图，已知直线AB，CD相交于点O，OE是射线，若∠1=30°，∠2=60°，则OE与AB 的位置关系是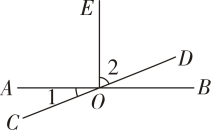
13. 如图，已知AC⊥BC于点C，CD⊥AB于点D，亮亮总结出了如下结论：
①线段AC的长表示点A到直线BC的距离；
②线段CD的长表示点C到直线AB的距离；
③线段AD的长表示点A到直线CD的距离；
④∠ACD是∠BCD的余角．
亮亮总结的结论正确的有 个．
14. 已知∠AOC和∠BOD是一组对顶角，若∠AOC＝40°，则∠BOD＝ ．15. 如图，直线a、b交于点O，若 ， 则 ．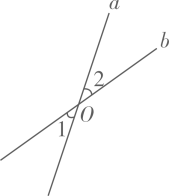
16. 如图，直线EF分别交∠AOB的两边于C，D两点，图中有对对顶角，分别是
三、解答题（共8题，共66分）
-
17. 如图，直线AB、CD相交于点O，OE平分∠AOD，OF⊥CD，∠AOE=70°，求∠BOF的度数.
18. 如图，直线、相交于点O，且于O，平分 ， ， 求的度数.
19. 如图，直线AB与直线CD相交于点O，∠COE＝135°，∠BOD＝45°，则OE⊥AB．请说明理由（补全解答过程）．
解：∵∠AOC＝∠BOD＝45°（ ）；
∴∠AOE＝ ▲ ＝（ °）；
∴OE⊥AB（对顶角相等）．
20. 如图，直线AB，CD相交于点O，OM⊥AB于点O．
(1)、若∠BOC=2∠AOC，求∠BOD的度数．(2)、若∠1=∠2，则ON与CD垂直吗？如果垂直，请说明理由．21. 如图，直线AB，CD相交于点O，OM⊥AB．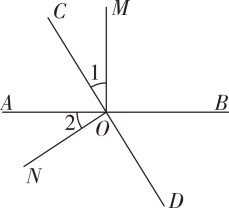
(1)、若∠1=40°，∠2= 30°，求∠NOD的度数．(2)、如果∠1=∠2，那么ON与CD互相垂直吗？请说明理由．22. 如图，直线AE与CD相交于点B，BF⊥AE．
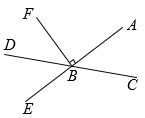(1)、若∠DBE＝60°，求∠FBD的度数；(2)、猜想∠CBE与∠DBF的数量关系，并说明理由．
