(人教版)2024年中考数学一轮复习 图形的变化--轴对称变换 练习题
试卷更新日期:2023-11-26 类型:一轮复习
一、选择题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点的坐标为 , 则点关于轴对称的点为( )A、 B、 C、 D、3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
2. 已知点的坐标为 , 则点关于轴对称的点为( )A、 B、 C、 D、3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,由正六边形和正三角形组成的图形为轴对称图形,该图形的对称轴的条数为( )
4. 如图,由正六边形和正三角形组成的图形为轴对称图形,该图形的对称轴的条数为( ) A、 B、 C、 D、5. 围棋起源于中国.古代称之为“弈”,至今已有多年历史.年月,世界围棋冠军柯洁与人工智能机器人进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、
A、 B、 C、 D、5. 围棋起源于中国.古代称之为“弈”,至今已有多年历史.年月,世界围棋冠军柯洁与人工智能机器人进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、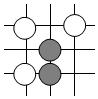 B、
B、 C、
C、 D、
D、 6. 下列是正方体的四种平面展开图,其中展开图是轴对称图形的是( )A、
6. 下列是正方体的四种平面展开图,其中展开图是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 平面直角坐标系中点关于轴的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、9. 下列图案是中心对称图形但不是轴对称图形的是( )A、
7. 平面直角坐标系中点关于轴的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 在平面直角坐标系中,若点P的坐标为 , 则点P关于y轴对称的点的坐标为( )A、 B、 C、 D、9. 下列图案是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )A、
10. 古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 .
 12. 在平面直角坐标系xOy中,点关于y轴对称的点的坐标为.13. 在平面直角坐标系中,点 与点 关于 轴对称,则 的值是 .14. 如图, 是圆 的弦, ,垂足为点 ,将劣弧 沿弦 折叠交于 的中点 ,若 ,则圆 的半径为.
12. 在平面直角坐标系xOy中,点关于y轴对称的点的坐标为.13. 在平面直角坐标系中,点 与点 关于 轴对称,则 的值是 .14. 如图, 是圆 的弦, ,垂足为点 ,将劣弧 沿弦 折叠交于 的中点 ,若 ,则圆 的半径为. 15. 将一个矩形 纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=.
15. 将一个矩形 纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=.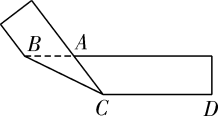
三、解答题
-
16. 折叠如图所示的直角三角形纸片ABC,使点C落在AB上的点E处,折痕为AD(点D在BC边上),用直尺和圆规画出折痕AD.(保留作图痕迹,不写作法).
 17. 如图,把一张长方形的纸片按如图所示样子折叠,则重合部分的是什么形状,并说明理由.
17. 如图,把一张长方形的纸片按如图所示样子折叠,则重合部分的是什么形状,并说明理由. 18. 如图,在矩形中, , , 点E是边上的一点,连接 , 将沿翻折,使点D恰好落在边上的点F处,求的值.
18. 如图,在矩形中, , , 点E是边上的一点,连接 , 将沿翻折,使点D恰好落在边上的点F处,求的值. 19. 如图,在矩形ABCD中,E是AB的中点,F是为射线AD上的一个动点,将△AEF沿EF折叠得到△HEF,连接AC,分别交EF和直线EH于点N,M,已知∠BAC= , ,若△EMN与△AEF相似,则AF的长为多少?
19. 如图,在矩形ABCD中,E是AB的中点,F是为射线AD上的一个动点,将△AEF沿EF折叠得到△HEF,连接AC,分别交EF和直线EH于点N,M,已知∠BAC= , ,若△EMN与△AEF相似,则AF的长为多少?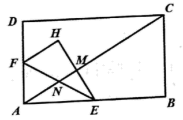
四、综合题
-
20. 如图,直线与反比例函数的图象交于 , 两点.
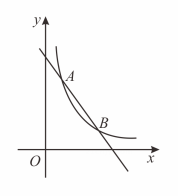 (1)、求的值;(2)、在轴上找一点 , 连接 , , 使的值最小,求点的坐标.21. 如图,在中, , 、分别为、的中点,连接并延长至点 , 且 , 点为直线上的一个动点.
(1)、求的值;(2)、在轴上找一点 , 连接 , , 使的值最小,求点的坐标.21. 如图,在中, , 、分别为、的中点,连接并延长至点 , 且 , 点为直线上的一个动点. (1)、求证:四边形为菱形.(2)、若 , 菱形的面积为24,求的最小值.
(1)、求证:四边形为菱形.(2)、若 , 菱形的面积为24,求的最小值.