（人教版）2024年中考数学一轮复习图形的性质--命题和证明练习题

试卷更新日期：2023-11-26 类型：一轮复习

进入出卷网下载

一、选择题

1. 下面命题正确的是（）

A、矩形对角线互相垂直
B、方程 $x^{2} = 14 x$ 的解为 $x = 14$ C、六边形内角和为 $540 °$ D、一对直角三角形，有一组斜边和直角边对应相等，则这两个直角三角形全等

查看试题解析
2. 下列命题：①若 $| a | = | b |$ ，则 $a = b$ ；②同旁内角互补，两直线平行；③相等的角是对顶角；④无限小数是无理数.其中假命题的是（）

A、①② B、②③ C、②③④ D、①③④

查看试题解析
3. 命题：已知 $△ A B C$ ， $A B = A C$ ．求证： $∠ B < 90 °$ ．运用反证法证明这个命题时，第一步应假设（）成立

A、 $A B \neq A C$ B、 $∠ B > 90 °$ C、 $∠ B \geq 90 °$ D、 $A B \neq A C$ 且 $∠ B \geq 90 °$

查看试题解析
4. 数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（）

A、射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”； B、车轮做成圆形，应用了“圆是中心对称图形”； C、学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”； D、地板砖可以做成矩形，应用了“矩形对边相等”．

查看试题解析
5. 能说明命题“对于任意实数 $a$ ， $| a | > - a$ ”是假命题的反例为（）

A、 $a = \frac{1}{3}$ B、 $a = - 2$ C、 $a = 1$ D、 $a = \sqrt{3}$

查看试题解析
6. 下列说法正确的是（）

A、“清明时节雨纷纷”是必然事件 B、为了了解一批灯管的使用寿命，可以采用普查的方式进行 C、一组数据2，5，4，5，6，7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 $S_{甲}^{2} = 0.02$ ， $S_{乙}^{2} = 0.01$ ，那么乙组队员的身高比较整齐

查看试题解析
7. 能说明“锐角 $α$ ，锐角 $β$ 的和是锐角”是假命题的例证图是（）.

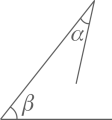A、 B、 C、 D、

查看试题解析
8. 下列命题正确的是（）

A、圆心角的度数等于圆周角的度数的2倍 B、有两边相等的平行四边形是菱形 C、若 $a + b < 0$ ， $a b > 0$ ，且 $a - 2 b \geq 0$ ，则 $\frac{a}{b}$ 有最大值2 D、若 $c < \frac{1}{2}$ ，则抛物线 $y = \frac{1}{2} x^{2} + x + c$ 与x轴没有交点

查看试题解析
9. 下列命题中，是真命题的是（）

A、长度相等的弧是等弧 B、如果|a|=1，那么a=1 C、两直线平行，同位角相等 D、如果x＞y ，那么－2x＞－2y

查看试题解析
10. 用反证法证明命题：“在三角形中，至多有一个内角是直角”，正确的假设是（）

A、在三角形中，至少有一个内角是直角 B、在三角形中，至少有两个内角是直角 C、在三角形中，没有一个内角是直角 D、在三角形中，至多有两个内角是直角

查看试题解析

二、填空题

11. 用一个a的值说明命题“若 $a > 0$ ，则 $a^{2} > \frac{1}{a}$ ”是错误的，这个值可以是 $a =$ ．

查看试题解析
12. 用一个a的值说明“若a是实数，则2a一定比a大”是错误的，这个值可以是．

查看试题解析
13. 能说明命题“若x＞-4，则x²＞16”是假命题的一个反例可以是.

查看试题解析
14. 命题“如果a+b=0，那么a，b互为相反数”的逆命题为.

查看试题解析
15. 命题“若 $a c = b c$ ，则 $a = b$ ”是命题.（填“真”或“假”）.

查看试题解析

三、解答题

16. 已知 $a + b + c = 0$ ，且 $\frac{b - c}{a} + \frac{c - a}{b} + \frac{a - b}{c} = 0$ ，求证： $\frac{b c + b - c}{b^{2} c^{2}} + \frac{c a + c - a}{c^{2} a^{2}} + \frac{a b + a - b}{a^{2} b^{2}} = 0$ ．

查看试题解析
17. 同学们，你们知道吗？三角形的内角和不一定是180°.
德国数学家黎曼创立的黎曼几何中描述：在球面上选三个点连线构成一个三角形，这个三角形的内角和大于180°.黎曼几何开创了几何学的新领域，近代黎曼几何在广义相对论里有着重要的应用.同样，在俄国数学家罗巴切夫斯基发表的新几何（简称罗氏几何）中，描述了在双曲面里画出的三角形，它的内角和永远小于180°.罗氏几何在天体理论中有着广泛的应用.而我们所学习的欧氏几何中描述“在平面内，三角形的内角和等于180°”是源于古希腊数学家欧几里得编写的《原本》.欧几里得创造的公理化体系影响了世界2000多年，是整个人类文明史上的里程碑.

请你证明：在平面内，三角形的内角和等于180°.要求画出图形，写出已知、求证和证明.

查看试题解析
18. 下面是小文设计的“过圆外一点作圆的切线”的作图过程．
已知： $⊙ O$ 和圆外一点P．
求作：过点P的 $⊙ O$ 的切线．
作法：①连接 $O P$ ；作 $O P$ 的垂直平分线与 $O P$ 交于点M；②以 $O M$ 半径作 $⊙ M$ ，交 $⊙ O$ 于点A，B；③作直线 $P A ， P B$ ；
所以直线 $P A ， P B$ 为 $⊙ O$ 的切线．
请利用尺规作图补全小文的作图过程，并完成下面的证明．
证明：连接 $O A ， O B$ ．
∵ $O P$ 为 $⊙ M$ 的直径，
∴ $∠ O A P = ∠$ ▲ = ▲ $°$ （）（填推理的依据）．
∴ $O A ⊥ A P ， O B ⊥ B P$
∵ $O A ， O B$ 为 $⊙ O$ 半径，
∴直线 $P A ， P B$ 为 $⊙ O$ 的切线．（）（填推理的依据）．

查看试题解析
19. 证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半（要求：自己作图并写出已知、求证、证明）

查看试题解析

四、综合题

20. 已知：如图，AB是⊙O的直径，AC是⊙O的弦，过点C的直线交AB延长线于点D，给出下列信息：
①∠A＝30°；
②CD是⊙O的切线；
③OB＝BD．

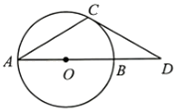(1)、请在上述3条信息中选择其中两条作为条件，剩下的一条作为结论．你选择的条件是 ▲ ，结论是 ▲ （只要填写序号）．判断结论是否正确，并说明理由；

(2)、在（1）的条件下，若CD＝3 $\sqrt{3}$ ，求 $\overset{⌢}{B C}$ 的长度．

查看试题解析
21. 已知：如图，直线l ，和直线外一点P ．
求作：过点P作直线PC ，使得PC∥l ，

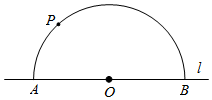
作法：①在直线l上取点O ，以点O为圆心，OP长为半径画圆，交直线l于A ， B两点；

②连接AP ，以点B为圆心，AP长为半径画弧，交半圆于点C；

③作直线PC ．

直线PC即为所求作．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明：
证明：连接BP ．

∵BC＝AP ，

∴ $\overset{⌢}{B C} =$ ▲ ．

∴∠ABP＝∠BPC（）（填推理依据）．

∴直线PC∥直线l ．

查看试题解析
22. 如图，在△ABC中，点D，E分别在AB，AC上.

(1)、若BD=CE，CD=BE，求证AB=AC；

(2)、分别将“BD=CE”记为①，“CD=BE”记为②，“AB=AC”记为③.以①、③为条件，②为结论构成命题1，以②、③为条件，①为结论构成命题2.则命题1是命题，命题2是命题(选择“真”或“假“填入空格)

查看试题解析
23. 为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
教职工气排球比赛比分胜负表

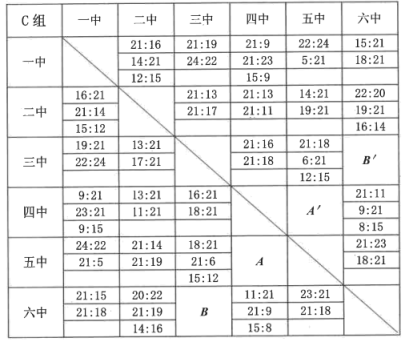(1)、根据表中数据可知，一中共获胜场，“四中VS五中”的比赛获胜可能性最大的是；

(2)、若 $A$ 处的比分是21∶10和21∶8，并且参加决赛的队伍是二中和五中，则 $B^{'}$ 处的比分可以是和；（两局结束比赛，根据自己的理解填写比分）；

(3)、若 $A^{'}$ 处的比分是10∶21和8∶21， $B$ 处的比分是21∶18，15∶21，15∶12，那么实力最强的是哪两支队伍，请说明理由．

查看试题解析

（人教版）2024年中考数学一轮复习 图形的性质--命题和证明 练习题

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2024年中考数学一轮复习图形的性质--命题和证明练习题