2023年浙教版数学七年级上册6.3线段的长短比较 同步测试（提升版）
试卷更新日期：2023-11-26 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 如图所示，某同学的家在处，他想尽快赶到附近处搭顺风车．他选择第②条路线，用几何知识解释其道理正确的是（ ）
A、两点确定一条直线 B、两点之间，线段最短 C、垂线段最短 D、经过一点有无数条直线2. 如图，某同学用剪刀沿虚线将三角形剪掉一个角，发现四边形的周长比原三角形的周长要小，能正确解释这一现象的数学知识是（ ）
A、两点确定一条直线 B、点动成线 C、直线是向两端无限延伸的 D、两点之间，线段最短3. 如图，从小明家A到学校B原有三条路线：路线①A﹣D﹣B；路线②A﹣E﹣B；路线③A﹣C﹣B ， 后又开通了一条直道，路线④A﹣B ， 这四条路线中路程最短的是（ ）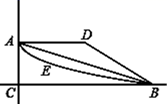
A、路线① B、路线② C、路线③ D、路线④4. 如图，小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分，发现剩下纸片的周长比原来的周长要小，能正确解释这一现象的数学知识是（ ）
A、两点之间，直线最短 B、经过一点，有无数条直线 C、两点确定一条直线 D、两点之间，线段最短5. 如图，从 点走到 点有三条路径，那么三条路径中最短的是（ ）
A、 B、 C、 D、三条路径一样长6. 下列说法错误的是（ ）A、 既不是正数也不是负数 B、经过两点有一条直线，并且只有一条直线 C、两点之间，线段最短 D、射线 与射线 是同一条射线7. 在下列生活、生产现象中，可以用基本事实“两点之间，线段最短”来解释的是（ ）①用两颗钉子就可以把木条固定在墙上；②在A、B两地之间架设电线时，总是尽可能沿线段AB架设；③植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上；④把弯曲的公路改直，就能缩短路程.
A、①② B、①③ C、②④ D、③④8. 如图1，A，B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小，图2中所示的C点即为所求的码头的位置，那么这样做的理由是（ ）
A、两直线相交只有一个交点 B、两点确定一条直线 C、两点之间，线段最短 D、经过一点有无数条直线9. 如图，把长方形沿虚线剪去一个角，得到一个五边形，则这个五边形的周长______原来长方形的周长，理由是______，横线上依次填入（ ）
A、大于：经过两点有一条直线，并且只有一条直线 B、大于：两点之间的所有连线中，线段最短 C、小于：经过两点有一条直线，并且只有一条直线 D、小于：两点之间的所有连线中，线段最短10. 为解决村庄灌溉问题，政府投资由水库向A，B，C，D，E这五个村庄铺设管道，现已知这五个村庄与水库以及村与村之间的距离(单位：km)如图所示，则把水库的水输送到这五个村庄铺设管道的总长度最短应是（ ）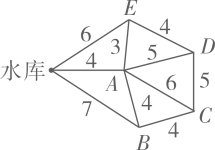
A、19km B、20km C、21 km D、22 km二、填空题（每空4分，共36分）
-
11. 如图，线段AB比折线AMB ， 理由.
12. 如图，从教室到图书馆总有少数同学不走人行道而横穿草坪，虽然明知不对，可他们还是要这样做，用我们所学的数学知识可以解释他们的动机：.
13. 如图，甲、乙两地之间有多条路可走，其中最短路线的走法序号是②-④，其理由是.
14. 如图所示，在一条笔直公路l的两侧，分别有A、B两个小区，为了方便居民出行，现要在公路l上建一个公共自行车存放点，使存放点到A、B小区的距离之和最小，你认为存放点应该建在处（填“C”“E”或“D”），理由是 ．
15. 如图，在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和OA+OB+OC+OD最小，正确的作法是连接AC、BD交于点O，则点O就是要找的点，请你用所学过的数学知识解释这一道理.
16. 如图，剪去四边形的“一角”，得到一个五边形，这个五边形的周长一定这个四边形的周长（填“大于”，“小于”或“等于”），依据是.
三、解答题（共5题，共54分）
-
17. 读句子画图：如图A、B、C、D在同一平面内
过点A、D画直线
画射线
连结
连接和相交于点E
连结并延长到F ， 使
18. 平面上有四个点 ， 按照以下要求作图（保留作图痕迹）：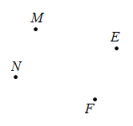
(1)、连接 ， 并延长至G，使；(2)、作射线；(3)、作直线 ， 并在直线MF上确定点H，使得最短．
