2023年浙教版数学七年级上册6.2线段、射线和直线 同步测试（培优版）
试卷更新日期：2023-11-26 类型：同步测试
一、选择题（每题4分，共40分）
-
1. 下列语句正确的是（ ）A、延长线段到 ， 使 B、反向延长线段 ， 得到射线 C、取射线的中点 D、连接A、B两点，使线段过点2. 下列说法正确的是（ ）A、直线AB与直线BA不是同一条直线 B、射线AB与射线BA是同一条射线 C、延长线段AB和延长线段BA的含义一样 D、线段AB与线段BA是同一条线段3. 如图，下列说法错误的是（ ）
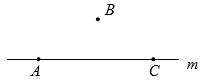A、点在直线上，点在直线外 B、射线与射线不是同一条射线 C、直线还可以表示为直线或直线 D、图中有直线3条，射线2条，线段1条4. 如图，下列表述错误的是（ ）
A、线段AB和射线AC都是直线AB的一部分 B、点D在直线AB上 C、直线AC和直线BD相交于点B D、直线BD不经过点A5. 有三个点A，B，C，过其中每两个点画直线，可以画出直线（ ）A、1条 B、2条 C、1条或3条 D、无法确定6. 如图，以A为一个端点的线段共有（ ）
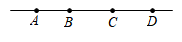A、1条 B、2条 C、3条 D、4条7. 如图所示图形中，共有（ ）条线段．
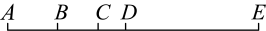A、10 B、12 C、15 D、308. 如图，AB是一段高铁行驶路线图图中字母表示的5个点表示5个车站在这段路线上往返行车，需印制（ ）种车票．
A、10 B、11 C、20 D、229. 拼尽全力挥动翅膀，才能在常仰望的天空中去拥抱梦想.如图中展翅欲飞的小鸟是利用直尺画出线段及其延长线构成的，就该图中出现的线段、直线、射线的条数而言（ ）
A、线段最多 B、直线最多 C、射线最多 D、射线最少10. 棋盘上有黑、白两色棋子若干，如果两颗棋子连成的直线上只有颜色相同的棋子，我们就称“同棋共线”．右图中“同棋共线”的直线共有（ ）
A、8条 B、10条 C、12条 D、16条二、填空题（每空5分，共35分）
-
11. 直线AB，BC，CA的位置关系如下所示，得出下列语句：
①点B在直线BC上；②直线AB经过点C；③直线AB， BC，CA两两相交；④点B是直线AB，BC的交点．以上语句正确的有(只填写序号)
12. 王小毛同学做教室卫生时，发现座位很不整齐，他思考了一下，将第一座和最后一座固定之后，沿着第一座最后一座这条线就把座位摆整齐了！他利用了数学原理： ．
13. 某高铁线路为往返于A市和E市，全长106千米，全线共设A、B、C、D、E五个车站，任意两站之间的距离都不相等，高铁集团要为乘客准备种车票，有种票价．14. 如图，棋盘上有黑、白两色棋子若干，若直线l经过3枚颜色相同的棋子，则这样的直线共有条．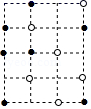
15. 如图图中有a条直线，b条射线，c条线段，则a+b－c的值等于 ．
16. 如图，点 ， ， ， ， 在线段上，则图中共有条线段．
三、解答题（共3题，共45分）
-
17. 已知：四点A、B、C、D的位置如图所示，根据下列语句，画出图形.
(1)、画直线、射线相交于点O，画线段；(2)、图中以字母A、B、C、D、O为端点的线段共有条.18. 若直线上有两个点，则以这两点为端点可以确定一条线段．请仔细观察图形，解决下列问题：
(1)、如图1，直线l上有3个点A，B，C，则可以确定条线段．(2)、如图2，直线l上有4个点A，B，C，D，则可以确定条线段．(3)、若直线l上有n个点，一共可以确定多少条线段？请写出解题过程．19. 如图
(1)、【观察思考】如图线段AB上有两个点C、D，分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点（包括端点），则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），请你应用上述模型构建，求一共要进行多少场比赛？