(人教版)2024年中考数学一轮复习 图形的性质--圆 练习题
试卷更新日期:2023-11-25 类型:一轮复习
一、选择题
-
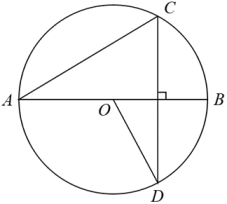
1. 若扇形的圆心角为 , 半径为 , 则它的弧长为( )A、 B、 C、 D、2. 如图,是直径, , 则为( )
 A、 B、 C、 D、3. 如图,、、是的切线,切点分别是、、若 , , 则的长是( )
A、 B、 C、 D、3. 如图,、、是的切线,切点分别是、、若 , , 则的长是( ) A、 B、 C、 D、4. 如图,分别与相切于A、B两点,连接 , 若 , 则的度数为( )
A、 B、 C、 D、4. 如图,分别与相切于A、B两点,连接 , 若 , 则的度数为( )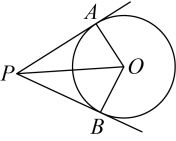 A、 B、 C、 D、5. 如图,是的直径,若 , 则的度数为( )
A、 B、 C、 D、5. 如图,是的直径,若 , 则的度数为( ) A、 B、 C、 D、6. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出米的螺旋曲线.在平面直角坐标系中,依次以这组数为半径作的圆弧 , 得到一组螺旋线,连接 , 得到一组螺旋折线,如图所示.已知点的坐标分别为 , 则点的坐标为( )
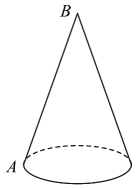
A、 B、 C、 D、6. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出米的螺旋曲线.在平面直角坐标系中,依次以这组数为半径作的圆弧 , 得到一组螺旋线,连接 , 得到一组螺旋折线,如图所示.已知点的坐标分别为 , 则点的坐标为( ) A、 B、 C、 D、7. 如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )
A、 B、 C、 D、7. 如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )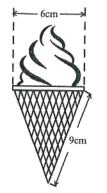 A、 B、 C、 D、8. 如图,是的弦,C是上一点, , 垂足为D , 若 , 则( )
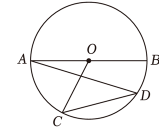
A、 B、 C、 D、8. 如图,是的弦,C是上一点, , 垂足为D , 若 , 则( ) A、 B、 C、 D、9. 如图, , 为的两条弦,、分别为 , 的中点,的半径为若 , 则的长为( )
A、 B、 C、 D、9. 如图, , 为的两条弦,、分别为 , 的中点,的半径为若 , 则的长为( ) A、 B、 C、 D、10. 某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 , 母线长为30 , 为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )
A、 B、 C、 D、10. 某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为 , 母线长为30 , 为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是( )v
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
 12. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.13. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .
12. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.13. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .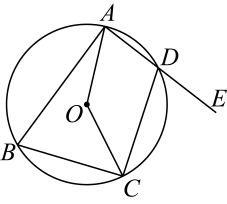 14. 如图,内接于 , 是的直径,点是上一点, , 则 .
14. 如图,内接于 , 是的直径,点是上一点, , 则 .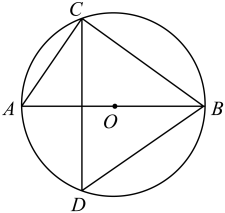 15. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留)
15. 如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是米.(结果保留)
三、解答题
-
16. 如图,在⊙O中,ACOB,∠BAO=25°,求∠BOC的度数.
 17. 如图, 的弦 相交于点P,且 .求证 .
17. 如图, 的弦 相交于点P,且 .求证 .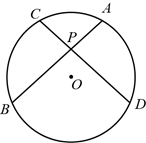 18. 已知:如图,四边形是的内接四边形,直径交边于点 , 、的延长线相交于点连接 , 若 .
18. 已知:如图,四边形是的内接四边形,直径交边于点 , 、的延长线相交于点连接 , 若 .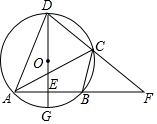 (1)、求证:;(2)、若 , , 求半径.19. 如图,四边形OACB的顶点A,B,C在以点O为圆心的同一个圆上,点C是的中点,连接OC并延长交圆O的切线BD于点D ,过点B作O的切线交OC的延长线于点D,已知∠D=30°.
(1)、求证:;(2)、若 , , 求半径.19. 如图,四边形OACB的顶点A,B,C在以点O为圆心的同一个圆上,点C是的中点,连接OC并延长交圆O的切线BD于点D ,过点B作O的切线交OC的延长线于点D,已知∠D=30°. (1)、求∠CBD的度数;(2)、判断四边形OACB的形状,并说明理由.
(1)、求∠CBD的度数;(2)、判断四边形OACB的形状,并说明理由.四、综合题
-
20. 如图,⊙ 中,弦 与 相交于点E, ,连接 .

求证:
(1)、 ;(2)、 .21. 如图,PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.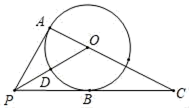 (1)、求证:∠APO=∠CPO;(2)、若⊙O的半径为3,OP=6,∠C=30°,求PC的长.
(1)、求证:∠APO=∠CPO;(2)、若⊙O的半径为3,OP=6,∠C=30°,求PC的长.