(人教版)2024年中考数学一轮复习 图形的性质-图形认识初步 练习题
试卷更新日期:2023-11-25 类型:一轮复习
一、选择题
-
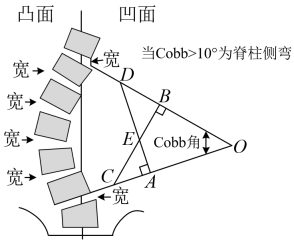
1. 如图是脊柱侧弯的检测示意图,在体检时为方便测出Cobb角的大小,需将转化为与它相等的角,则图中与相等的角是( )
 A、 B、 C、 D、2. 下面是由七巧板拼成的图形(只考虑外形,忽略内部轮廓),其中轴对称图形是( )
A、 B、 C、 D、2. 下面是由七巧板拼成的图形(只考虑外形,忽略内部轮廓),其中轴对称图形是( )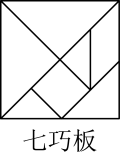 A、
A、 B、
B、 C、
C、 D、
D、 3. 下图中用量角器测得的度数是( )
3. 下图中用量角器测得的度数是( ) A、 B、 C、 D、4. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A、 B、 C、 D、4. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( ) A、强 B、富 C、美 D、高5. 如图,直线 , 一个三角板的直角顶点在直线a上,两直角边均与直线b相交, , 则( )
A、强 B、富 C、美 D、高5. 如图,直线 , 一个三角板的直角顶点在直线a上,两直角边均与直线b相交, , 则( )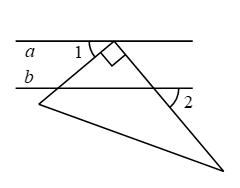 A、 B、 C、 D、6. 若 ,则 的余角为( )A、30° B、40° C、50° D、140°7. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
A、 B、 C、 D、6. 若 ,则 的余角为( )A、30° B、40° C、50° D、140°7. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( ) A、
A、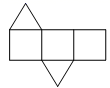 B、
B、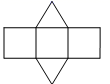 C、
C、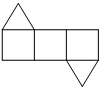 D、
D、 8. 如图,、、是的切线,切点分别是、、若 , , 则的长是( )
8. 如图,、、是的切线,切点分别是、、若 , , 则的长是( ) A、 B、 C、 D、9. 如图,围绕在正方形四周的四条线段a,b,c,d中,长度最小的是( )
A、 B、 C、 D、9. 如图,围绕在正方形四周的四条线段a,b,c,d中,长度最小的是( ) A、a B、b C、c D、d10. 中国古代数学著作《九章算术》在世界数学史上首次正式引入负数,书中记载:“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,如果数轴上有表示数字3和的两个点分别是点A和点B,则点A和点B之间的距离是( )A、1 B、 C、 D、5
A、a B、b C、c D、d10. 中国古代数学著作《九章算术》在世界数学史上首次正式引入负数,书中记载:“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,如果数轴上有表示数字3和的两个点分别是点A和点B,则点A和点B之间的距离是( )A、1 B、 C、 D、5二、填空题
-
11. 计算: .12. 如图,某一时刻在灯塔处观测到货轮在它的北偏东方向,同时又观测到客轮在它的东南方向,则的度数是 .
 13. 一艘船在A处遇险后向相距的B处的救生船报警.用方向和距离描述遇险船相对于救生船的位置是.
13. 一艘船在A处遇险后向相距的B处的救生船报警.用方向和距离描述遇险船相对于救生船的位置是. 14. 如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为
14. 如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为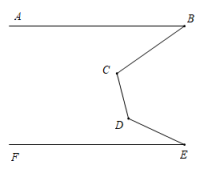 15. 如图,点D是线段AB的中点,C是线段AD的中点,若AB=8cm,则CD=cm.
15. 如图,点D是线段AB的中点,C是线段AD的中点,若AB=8cm,则CD=cm.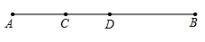
三、解答题
-
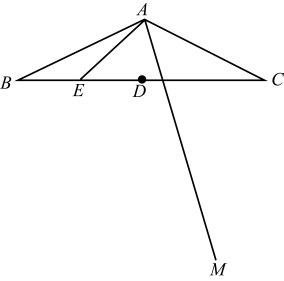
16. 如图所示,A、D、B、E四点在同一条直线上,若AD=BE,∠A=∠EDF,∠E+∠CBE=I80°,求证:AC=DF.
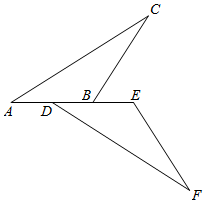 17. 如图, , , 点是延长线上一点,连接 , 点和点关于直线对称,连接交于点 , 连接 , , .
17. 如图, , , 点是延长线上一点,连接 , 点和点关于直线对称,连接交于点 , 连接 , , .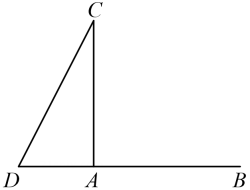 (1)、依题意补全图形,并求的度数;(2)、用等式表示线段 , 和之间的数量关系,并证明.18. 如图,在凹四边形中, , , , 求的度数.
(1)、依题意补全图形,并求的度数;(2)、用等式表示线段 , 和之间的数量关系,并证明.18. 如图,在凹四边形中, , , , 求的度数.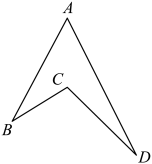
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求的度数.
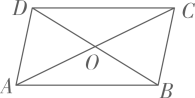
19. 如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别为OD、OB的中点,连接CE、AF.求证:CE=AF.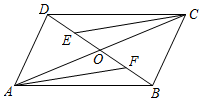
四、综合题
-
20. 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.
 (1)、若∠B=40°,求∠CDE的度数.(2)、若DE=4,试添加一个条件,并求出BC的长度.
(1)、若∠B=40°,求∠CDE的度数.(2)、若DE=4,试添加一个条件,并求出BC的长度.