（人教版）2024年中考数学一轮复习函数-二次函数练习题

试卷更新日期：2023-11-25 类型：一轮复习

进入出卷网下载

一、选择题

1. 将二次函数 $y = - (x - k)^{2} + k + 1$ 的图象向右平移 $1$ 个单位，再向上平移 $2$ 个单位后，顶点在直线 $y = 2 x + 2$ 上，则 $k$ 的值为（）

A、 $2$ B、 $1$ C、 $0$ D、 $- 1$

查看试题解析
2. 抛物线 $y = \frac{1}{2} x^{2} - 2$ 一定经过点（）

A、 $(0 ， 2)$ B、 $(2 ， 0)$ C、 $(4 ， 0)$ D、 $(0 ， 4)$ ．

查看试题解析
3. 下列 $y$ 关于 $x$ 的函数中，一定是二次函数的是（）

A、 $y = (a + 2) x^{2} + 1$ B、 $y = \frac{1}{x^{2}} + 1$ C、 $y = (x + 2) (x + 1) - x^{2}$ D、 $y = 2 x^{2} + 3 x$

查看试题解析
4. 将抛物线y＝x²-6x+5向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）

A、y＝（x-4）²-6 B、y＝（x-1）²-3 C、y＝（x-2）²-2 D、y＝（x-4）²-2

查看试题解析
5. 抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ， $a ， b ， c$ 为常数且 $c > 0$ ）的对称轴为 $x = - 2$ ，过点 $(1 ， - 2)$ 和点 $(x_{0} ， y_{0})$ ．有下列结论：① $a < - \frac{2}{5}$ ；②对任意实数 $m$ ，都有 $a m^{2} + (m + 2) b \leq 4 a$ ；③若 $x_{0} > - 4$ ，则 $y_{0} > c$ ．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 已知实心球运动的高度 $y (m)$ 与水平距离 $x (m)$ 之间的函数关系是 $y = - {(x - 1)}^{2} + 4$ ，则该同学此次投掷实心球的成绩是（）

A、 $2 m$ B、 $3 m$ C、 $3.5 m$ D、 $4 m$

查看试题解析
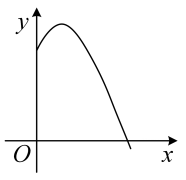7. 若抛物线 $y = a x^{2} + b x + c (a > 0)$ 经过第四象限的点 $(1, - 1)$ ），则关于x的方程 $a x^{2} + b x + c = 0$ 的根的情况是（）

A、有两个大于1的不相等实数根 B、有两个小于1的不相等实数根 C、有一个大于1另一个小于1的实数根 D、没有实数根

查看试题解析
8. 把函数 $y = - \frac{1}{2} x^{2}$ 的图象，经过怎样的平移变换以后，可以得到函数 $y = - \frac{1}{2} {(x - 1)}^{2} + 1$ 的图象（）

A、向左平移 $1$ 个单位，再向下平移 $1$ 个单位 B、向左平移 $1$ 个单位，再向上平移 $1$ 个单位 C、向右平移 $1$ 个单位，再向上平移 $1$ 个单位 D、向右平移 $1$ 个单位，再向下平移 $1$ 个单位

查看试题解析
9. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
10. 已知抛物线 $y = x^{2} + k x - k^{2}$ 的对称轴在 $y$ 轴右侧，现将该抛物线先向右平移3个单位长度，再向上平移1个单位长度后，得到的抛物线正好经过坐标原点，则 $k$ 的值是（）

A、-5或2 B、-5 C、2 D、-2

查看试题解析

二、填空题

11. 将抛物线 $y = x^{2} + 6 x$ 向右平移 $4$ 个单位，得到的新抛物线表达式是．

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是直线 $x = 1$ ，如果此抛物线与 $x$ 轴的一个交点的坐标是 $(3 ， 0)$ ，那么抛物线与 $x$ 轴的另一个交点的坐标是．

查看试题解析
13. 已知抛物线 $y = (a - 1) x^{2} + 2 x$ 开口向下，那么 $a$ 的取值范围是．

查看试题解析
14. 二次函数 $y = x^{2}$ 的图象开口方向是（填“向上”或“向下”）.

查看试题解析
15. 二次函数 $y = - 2 x^{2} - 4 x + 5$ 的最大值是.

查看试题解析

三、解答题

16. 把二次函数y＝x²+bx+c的图象向下平移1个单位长度，再向左平移5个单位长度，所得的抛物线顶点坐标为（﹣3，2），求原抛物线相应的函数表达式.

查看试题解析
17. 已知抛物线 $y = x^{2} + b x + c$ 交 $x$ 轴于 $C$ ， $D$ 两点，其中点 $C$ 的坐标为 $(- 1 ， 0)$ ，对称轴为 $x = 1 .$ 点 $A$ ， $B$ 为坐标平面内两点，其坐标为 $A (\frac{1}{2} ， - 5)$ ， $B (4 ， - 5)$ ．

(1)、求抛物线的解析式及顶点坐标；

(2)、连接 $A B$ ，若抛物线 $y = x^{2} + b x + c$ 向下平移 $k (k > 0)$ 个单位时，与线段 $A B$ 只有一个公共点，求 $k$ 的取值范围．

查看试题解析
18. 在平面直角坐标系 $x O y$ 中，点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ 都在抛物线 $y = a x^{2} - 2 a x + 8 (a < 0)$ 上，且 $- 1 < x_{1} < 2$ ， $1 - m < x_{2} < m + 7$ ．

(1)、当 $m = - 2$ 时，比较 $y_{1}$ ， $y_{2}$ 的大小关系，并说明理由；

(2)、若存在 $x_{1}$ ， $x_{2}$ ，满足 $y_{1} = y_{2}$ ，求 $m$ 的取值范围．

查看试题解析
19. 端午节吃粽子是中华民族的传统习俗，市场上猪肉粽进价比豆沙粽进价每盒贵 $10$ 元，一盒猪肉粽加两盒豆沙粽进价为 $100$ 元．

(1)、求每盒猪肉粽和豆沙粽的进价；

(2)、在销售中，某商家发现当每盒猪肉粽售价为 $50$ 元时，每天可售出 $100$ 盒，若每盒售价提高 $1$ 元，则每天少售出 $2$ 盒．设每盒猪肉粽售价为 $a$ 元，销售猪肉粽的利润为 $w$ 元，求该商家每天销售猪肉粽获得的最大利润．

查看试题解析

四、综合题

20. 如图已知二次函数 $y = x^{2} + 4 x - 5$ 的图象及对称轴，限用无刻度直尺按下列要求作图：

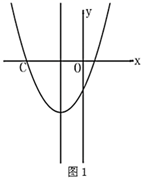
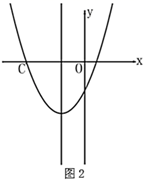(1)、在图1中作点 $A (- 4 ， - 5)$ ；

(2)、已知 $A (- 4 ， - 5)$ ，在图2中的对称轴上作点P，使 $C P - A P$ 最大；

查看试题解析
21. 如图，在平面直角坐标系中，已知二次函数 $y = x^{2} - 2 a x + 3 a$ ，顶点坐标为 $(x_{0} ， y_{0}) .$

(1)、若函数图象关于直线 $x = 1$ 对称，求函数的表达式；

(2)、求 $y_{0}$ 的最大值；

(3)、是否存在实数 $a$ ，使得当 $1 \leq x \leq 4$ 时，二次函数的最大值为最小值的 $3$ 倍，若存在，求出 $a$ ；若不存在，请说明理由．

查看试题解析
22. 在平面直角坐标系中，已知二次函数 $y = x^{2} - 2 m x + m^{2} - 4 m (m$ 为常数，且 $m \neq 0)$ ．

(1)、二次函数的图象经过坐标原点，求二次函数的表达式，并写出函数值 $y$ 随 $x$ 的增大而增大时 $x$ 的取值范围；

(2)、在 $(1)$ 的条件下，若点 $P (a ， b)$ 是二次函数图象上的一个动点，当 $a < x < 2$ 时， $b$ 的最大值为 $20$ ，求 $a$ 的值．

查看试题解析
23. 若二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (- 2 ， 0)$ ， $B (0 ， - 4)$ ，其对称轴为直线 $x = 1$ ，与 $x$ 轴的另一交点为 $C$ ．

(1)、求二次函数的表达式；

(2)、若点 $M$ 在直线 $A B$ 上，且在第四象限，过点 $M$ 作 $M N ⊥ x$ 轴于点 $N$ ．
①若点 $N$ 在线段 $O C$ 上，且 $M N = 3 N C$ ，求点 $M$ 的坐标；

②以 $M N$ 为对角线作正方形 $M P N Q ($ 点 $P$ 在 $M N$ 右侧 $)$ ，当点 $P$ 在抛物线上时，求点 $M$ 的坐标．

查看试题解析

（人教版）2024年中考数学一轮复习 函数-二次函数 练习题

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2024年中考数学一轮复习函数-二次函数练习题