（人教版）2024年中考数学一轮复习函数--反比例函数练习题

试卷更新日期：2023-11-25 类型：一轮复习

进入出卷网下载

一、选择题

1. 点 $(1 ， y_{1})$ ， $(2 ， y_{2})$ ， $(3 ， y_{3})$ ， $(4 ， y_{4})$ 在反比例函数 $y = \frac{4}{x}$ 图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ ， $y_{4}$ 中最小的是（）

A、 $y_{1}$ B、 $y_{2}$ C、 $y_{3}$ D、 $y_{4}$

查看试题解析
2. 已知点 $A (x_{1} ， - 6) ， B (x_{2} ， - 3 \sqrt{2}) ， C (x_{3} ， 3)$ 在反比例函数 $y = - \frac{18}{x}$ 的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（　　）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{1} < x_{3}$ C、 $x_{3} < x_{1} < x_{2}$ D、 $x_{3} < x_{2} < x_{1}$

查看试题解析
3. 对于反比例函数 $y = \frac{2}{x}$ ，下列说法不正确的是（）

A、图象关于原点成中心对称 B、经过点 $(1 ， 2)$ C、图象位于第一、三象限 D、当 $x > 0$ 时，y随x的增大而增大

查看试题解析
4. 如图，已知点 $P$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上．由点 $P$ 分别向 $x$ 轴， $y$ 轴作垂线段，与坐标轴围成的矩形部分面积为8．则 $k$ 的值为（）

A、4 B、－8 C、8 D、－4

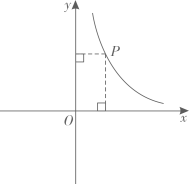查看试题解析
5. 反比例函数 $y = - \frac{3}{x}$ 的图象位于（）

A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限

查看试题解析
6. 已知点 $P (2 ， m)$ 是反比例函数 $y = \frac{6}{x}$ 图象上的一点，则 $m =$ （）

A、12 B、6 C、3 D、1

查看试题解析
7. 反比例函数 $y = \frac{k - 3}{x}$ 的图象过（3，6），则k的值为（）

A、15 B、18 C、21 D、25

查看试题解析
8. 下列函数中，y是x的反比例函数的是（）

A、 $y = \frac{3}{x^{2}}$ B、 $\frac{y}{x} = 3$ C、 $y = - 3 x$ D、 $y = - \frac{3}{x}$

查看试题解析
9. 下列函数中，y随x的增大而减少的是（）.

A、 $y = \frac{1}{x}$ B、 $y = \frac{2}{x}$ C、 $y = - \frac{3}{x} (x > 0)$ D、 $y = \frac{4}{x} (x < 0)$

查看试题解析
10. 已知点 $A (1 ， y_{1})$ ， $B (3 ， y_{2})$ 均在反比例函数 $y = \frac{k}{x}$ （k为常数）的图像上，若 $y_{1} > y_{2}$ ，则k的取值范围是（）

A、 $k < 0$ B、 $k > 0$ C、 $k > 1$ D、 $k < 1$

查看试题解析

二、填空题

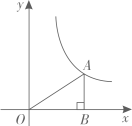
11. 已知反比例函数 $y = \frac{k - 1}{x}$ 的图象位于第二、四象限，则 $k$ 的取值范围是．

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (1 ， 3)$ 和点 $B (- 3 ， n)$ ，则 $n$ 的值为．

查看试题解析
13. 如图，点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，过点A作 $A B ⊥ x$ 轴于点B，若 $△ O A B$ 的面积为2，则该反比例函数的解析式是．

查看试题解析
14. 已知反比例函数 $y = - \frac{2}{x}$ 的图象经过点 $(- 6 ， a)$ ，则a的值为．

查看试题解析
15. 物理学中，在压力F不变的情况下，某物体承受的压强p与它的受力面积S成反比例函数关系，则下表中压强 $P_{1}$ 与 $P_{2}$ 的大小关系为： $P_{1}$ $P_{2}$ ．（填“ $>$ ”，“ $=$ ”或“ $<$ ”）
$S / m^{2}$
1
2
3
$P / P a$
$P_{1}$
300
$P_{2}$

查看试题解析

三、解答题

16. 如图，已知一次函数y₁＝kx＋b与反比例函数y₂＝ $\frac{m}{x}$ 的图象交于 $A (2 ， 4)$ 、 $B (- 4 ， n)$ 两点.分别求出y₁和y₂的解析式.

查看试题解析
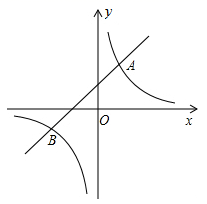17. 如图所示，已知 $A (- 4 ， 2)$ ， $B (n ， - 4)$ 是一次函数 $y = k x + b$ 图象与反比例函数 $y = \frac{m}{x}$ 图象的两个交点．

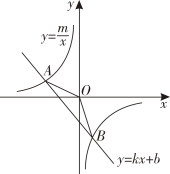(1)、求反比例函数和一次函数的表达式；

(2)、观察图象，当 $x$ 取何值时， $k x + b < \frac{m}{x}$ ．

查看试题解析
18. 某校科技小组在一次野外考察中遇到一片烂泥湿地 $.$ 为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木板，构筑成一条临时近道 $.$ 每块木板对地面的压强 $p (P a)$ 是木板面积 $S (m^{2})$ 的反比例函数，其图象如图所示．

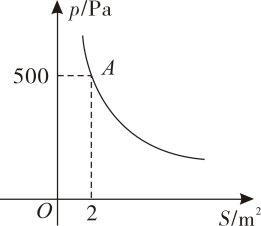(1)、请根据图象直接写出反比例函数的解析式；

(2)、如果要求压强不超过 $8000 P a$ ，求选用的木板的面积至少要多大？

查看试题解析
19. 如图，直线 $y = - x + 2$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于 $A (a ， 3)$ ， $B (3 ， b)$ 两点，过点 $A$ 作 $A C ⊥ x$ 轴于点 $G$ ，过点 $B$ 作 $B D ⊥ x$ 轴于点 $D$ ．

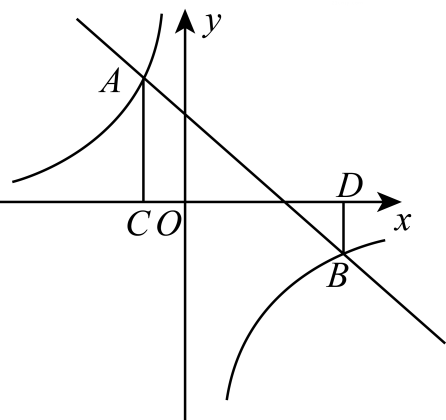(1)、求 $a$ ， $b$ 的值及反比例函数的解析式；

(2)、若点 $P$ 在直线 $y = - x + 2$ 上，且 $S_{△ A C P} = S_{△ B D P}$ ，请求出此时点 $P$ 的坐标．

查看试题解析

四、综合题

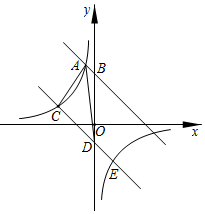
20. 已知双曲线 $y = \frac{k}{x}$ 的图像经过点A（3，4）.

(1)、求k的值；

(2)、请判断点B（2，6）是否在这个反比例函数的图象上，并说明理由.

查看试题解析
21. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 第一象限交于 $M (1 ， 6)$ 、 $N (6 ， m)$ 两点，点 $P$ 是 $x$ 轴负半轴上一动点，连接 $P M$ ， $P N$ ．

(1)、求一次函数的表达式；

(2)、若 $△ P M N$ 的面积为 $\frac{45}{2}$ ，求点 $P$ 的坐标；

(3)、在 $(2)$ 的条件下，若点 $E$ 为直线 $P M$ 上一点，点 $F$ 为 $y$ 轴上一点，是否存在这样的点 $E$ 和点 $F$ ，使得四边形 $E F N M$ 是平行四边形？若存在，直接写出点 $E$ 的坐标；若不存在，请说明理由．

查看试题解析
22. 设函数 $y_{1} = \frac{k}{x}$ （k＞0，k是常数），函数y₂＝-2x+7的图象交于点P（a₁ ， b₁），点Q（a₂ ， b₂）．

(1)、当a₁＝2时，求k的值．

(2)、若 $\frac{a_{1}}{a_{2}} = 2$ ，求 $\frac{b_{1}}{b_{2}}$ 的值．

(3)、若2＜x＜3时，总有y₁＜y₂ ，求k的取值范围．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $A B$ 与 $y$ 轴交于点 $B (0 ， 7)$ ，与反比例函数 $y = \frac{- 8}{x}$ 在第二象限内的图象相交于点 $A (- 1 ， a)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、将直线 $A B$ 向下平移 $9$ 个单位后与反比例函数的图象交于点 $C$ 和点 $E$ ，与 $y$ 轴交于点 $D$ ，求 $△ A C D$ 的面积；

(3)、设直线 $C D$ 的解析式为 $y = m x + n$ ，根据图象直接写出不等式 $m x + n \leq \frac{- 8}{x}$ 的解集．

查看试题解析

$S / m^{2}$	1	2	3
$P / P a$	$P_{1}$	300	$P_{2}$

（人教版）2024年中考数学一轮复习 函数--反比例函数 练习题

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2024年中考数学一轮复习函数--反比例函数练习题