(人教版)2024年中考数学一轮复习 函数--一次函数 练习题
试卷更新日期:2023-11-24 类型:一轮复习
一、选择题
-
1. 在平面直角坐标系中,下列函数的图象经过原点的是( )A、 B、 C、 D、2. 直线经过一、三、四象限,那么点在第几象限.( )A、四 B、三 C、二 D、一3. 如图,直线与x轴交点的横坐标为1,则关于x的方程的解为( ).
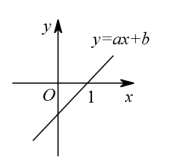 A、1 B、 C、2 D、4. 如果一次函数y=kx+b的图象经过第一、三、四象限,那么k、b应满足的条件是( )A、k>0,且b>0 B、k>0,且b<0 C、k<0,且b>0 D、k<0,且b<05. 某登山队大本营所在地的气温为 . 海拔每升高 , 气温下降 . 队员由大本营向上登高 , 气温为 , 则y与x的函数关系式为( )A、 B、 C、 D、6. 如图,在平面直角坐标系中,一次函数(a、b为常数,且)的图象与一次函数的图象相交于点P,若点P的纵坐标为8,则关于x,y的方程组的解是( )
A、1 B、 C、2 D、4. 如果一次函数y=kx+b的图象经过第一、三、四象限,那么k、b应满足的条件是( )A、k>0,且b>0 B、k>0,且b<0 C、k<0,且b>0 D、k<0,且b<05. 某登山队大本营所在地的气温为 . 海拔每升高 , 气温下降 . 队员由大本营向上登高 , 气温为 , 则y与x的函数关系式为( )A、 B、 C、 D、6. 如图,在平面直角坐标系中,一次函数(a、b为常数,且)的图象与一次函数的图象相交于点P,若点P的纵坐标为8,则关于x,y的方程组的解是( )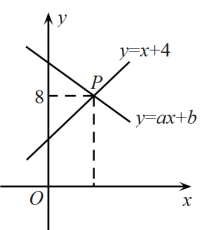 A、 B、 C、 D、7. 一次函数的图象不经过第三象限,则( )A、 , B、 , C、 , D、 ,8. 下列函数中,函数值y随x的增大而减小的是( )A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( )
A、 B、 C、 D、7. 一次函数的图象不经过第三象限,则( )A、 , B、 , C、 , D、 ,8. 下列函数中,函数值y随x的增大而减小的是( )A、 B、 C、 D、9. 在同一平面直角坐标系中,一次函数与的图象如图所示,则下列结论错误的是( ) A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为10. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、
A、随的增大而增大 B、 C、当时, D、关于 , 的方程组的解为10. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、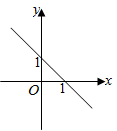 B、
B、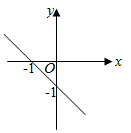 C、
C、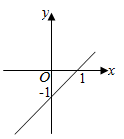 D、
D、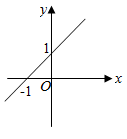
二、填空题
-
11. 关于x的一次函数 , 若y随x的增大而增大,且图象与y轴的交点在原点下方,则实数a的取值范围是.12. 已知一次函数的图象经过点和 , 则 .13. 若直线向上平移3个单位长度后经过点 , 则的值为 .14. 将直线 向下平移2个单位长度,平移后直线的解析式为.15. 在正比例函数 中,y的值随着x值的增大而增大,则点 在第象限.
三、解答题
-
16. 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地卸装货物用时 , 结束后,立即按原路以另一速度匀速返回,直至与慢车相遇,已知慢车的速度为 . 两车之间的距离与慢车行驶的时间的函数图象如图所示.
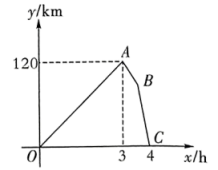 (1)、请解释图中点的实际意义;(2)、求出图中线段所表示的函数表达式;(3)、两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.17. 学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师现有甲、乙两种大型客车,它们的载客量和租金如表所示:
(1)、请解释图中点的实际意义;(2)、求出图中线段所表示的函数表达式;(3)、两车相遇后,如果快车以返回的速度继续向甲地行驶,求到达甲地还需多长时间.17. 学校通过劳动教育促进学生树德、增智、强体、育美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动到达农场后分组进行劳动,若每位老师带名学生,则还剩名学生没老师带;若每位老师带名学生,则有一位老师少带名学生劳动实践结束后,学校在租车总费用元的限额内,租用汽车送师生返校,每辆车上至少要有名老师现有甲、乙两种大型客车,它们的载客量和租金如表所示:甲型客车
乙型客车
载客量人辆
租金元辆
(1)、参加本次实践活动的老师和学生各有多少名?(2)、租车返校时,既要保证所有师生都有车坐,又要保证每辆车上至少有名老师,则共需租车辆;(3)、学校共有几种租车方案?最少租车费用是多少?18. 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用元与该水果的质量千克之间的关系如图所示;在乙商店购买该水果的费用元与该水果的质量千克之间的函数解析式为 . (1)、求与之间的函数解析式;(2)、现计划用元购买该水果,选甲、乙哪家商店能购买该水果更多一些?19. 为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
(1)、求与之间的函数解析式;(2)、现计划用元购买该水果,选甲、乙哪家商店能购买该水果更多一些?19. 为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:信息—
工程队
每天施工面积(单位:)
每天施工费用(单位:元)
甲
3600
乙
x
2200
信息二
甲工程队施工所需天数与乙工程队施工所需天数相等.
(1)、求x的值;(2)、该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于 . 该段时间内体育中心至少需要支付多少施工费用?四、综合题
-
20. 为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元?(2)、学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.21. 一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,如图表示两车行驶时间 (小时)与到甲地的距离 (千米)的函数图象,已知其中一个函数的表达式为 .
 (1)、求另一个函数表达式.(2)、求两车相遇的时间.22. 绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示.
(1)、求另一个函数表达式.(2)、求两车相遇的时间.22. 绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示. (1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?23. 许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨 , 的交点.点C为抛物线的顶点,点A,B在抛物线上, , 关于y轴对称.分米,点A到x轴的距离是分米,A,B两点之间的距离是4分米.
(1)、求生产成本y2(元)与产量x(kg)之间的函数关系式;(2)、求日利润为W(元)与产量x(kg)之间的函数关系式;(3)、当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?23. 许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨 , 的交点.点C为抛物线的顶点,点A,B在抛物线上, , 关于y轴对称.分米,点A到x轴的距离是分米,A,B两点之间的距离是4分米.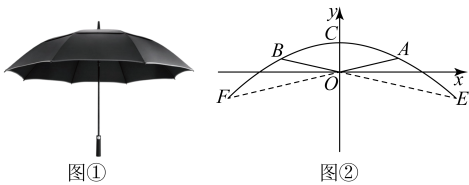 (1)、求抛物线的表达式;(2)、分别延长 , 交抛物线于点F,E,求E,F两点之间的距离;(3)、以抛物线与坐标轴的三个交点为顶点的三角形面积为 , 将抛物线向右平移个单位,得到一条新抛物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为 . 若 , 求m的值.
(1)、求抛物线的表达式;(2)、分别延长 , 交抛物线于点F,E,求E,F两点之间的距离;(3)、以抛物线与坐标轴的三个交点为顶点的三角形面积为 , 将抛物线向右平移个单位,得到一条新抛物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为 . 若 , 求m的值.