(人教版)2024年中考数学一轮复习 函数--函数基础知识 练习题
试卷更新日期:2023-11-24 类型:一轮复习
一、选择题
-
1. 下面的三个问题中都有两个变量:
矩形的面积一定,一边长与它的邻边长;
某村的耕地面积一定,人均耕地面积与全村总人口;
汽车的行驶速度一定,行驶路程与行驶时间 .
其中,两个变量之间的函数关系可以用形如为常数,的式子表示的是( )A、 B、 C、 D、2. 油箱中存油升,油从油箱中均匀流出,流速为升分钟,则油箱中剩余油量升与流出时间分钟的函数关系是( )A、 B、 C、 D、3. 甲、乙两种物质的溶解度y()与温度t()之间的对应关系如图所示,下列说法:①甲、乙两种物质的溶解度都随着温度的升高而增大;②当温度升高至时,甲的溶解度比乙的溶解度小;③当温度为时,甲、乙的溶解度都小于;④当温度为时,甲、乙的溶解度相同.其中正确结论的序号是( ) A、①② B、①③ C、①③④ D、②④4. 骑自行车是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程(km)与时间(h)的关系图象,观察图象得到下列信息,其中错误的是( )
A、①② B、①③ C、①③④ D、②④4. 骑自行车是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程(km)与时间(h)的关系图象,观察图象得到下列信息,其中错误的是( ) A、点表示出发4h,老刘共骑行80km B、老刘的骑行在0~2h的速度比3~4h的速度慢 C、0~2h老刘的骑行速度为15km/h D、老刘实际骑行时间为4h5. 函数中自变量x的取值范围在数轴上可表示为( )A、
A、点表示出发4h,老刘共骑行80km B、老刘的骑行在0~2h的速度比3~4h的速度慢 C、0~2h老刘的骑行速度为15km/h D、老刘实际骑行时间为4h5. 函数中自变量x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、 D、
D、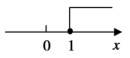 6. 某商品月份单个的进价和售价如图所示,则售出该商品单个利润最大的是( )
6. 某商品月份单个的进价和售价如图所示,则售出该商品单个利润最大的是( ) A、1月 B、2月 C、3月 D、4月7. 变量与的关系式是 , 当自变量时,因变量的值是( )A、-5 B、5 C、1 D、-18. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
A、1月 B、2月 C、3月 D、4月7. 变量与的关系式是 , 当自变量时,因变量的值是( )A、-5 B、5 C、1 D、-18. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )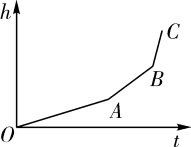 A、
A、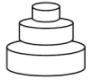 B、
B、 C、
C、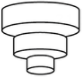 D、
D、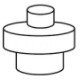 9. 变量x,y的一些对应值如下表:
9. 变量x,y的一些对应值如下表:…
-2
-1
0
1
2
3
…
…
-1
-0.5
0
0.5
1
1.5
…
根据表格中的数据规律,当时,y的值是( )
A、2 B、-2.5 C、-1.5 D、-210. 二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长,如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过14小时的节气是( )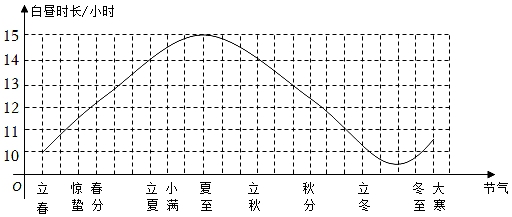 A、惊蛰 B、立夏 C、夏至 D、大寒
A、惊蛰 B、立夏 C、夏至 D、大寒二、填空题
-
11. 已知 , 那么 .12. 在函数中,自变量的取值范围是 .13. 在函数中,自变量x的取值范围是 .14. 在函数中,自变量x的取值范围为 .15. 函数y=2x+的自变量x的取值范围是.
三、解答题
-
16. 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
 17. 校运会上,每班选派一位男同学和一位女同学参加100米运球比赛,男同学甲与女同学乙同时从起点出发,运球沿同一路线匀速向终点前进,甲先到达终点放下球后立即原路返回接力乙同学,并与乙同学一起到达终点.甲、乙两位同学距出发地的路程y(米)与甲的运动时间x(秒)之间的函数关系如图所示.
17. 校运会上,每班选派一位男同学和一位女同学参加100米运球比赛,男同学甲与女同学乙同时从起点出发,运球沿同一路线匀速向终点前进,甲先到达终点放下球后立即原路返回接力乙同学,并与乙同学一起到达终点.甲、乙两位同学距出发地的路程y(米)与甲的运动时间x(秒)之间的函数关系如图所示.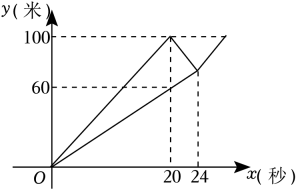 (1)、求甲同学从终点返回到与乙同学相遇过程中,甲同学距出发地的路程y与x之间的函数关系式.(2)、若甲同学与乙同学相遇后,改由甲同学运球,两人仍以甲第一次到达终点前的速度一起前往终点,则两人到达终点的时间为 秒.18. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
(1)、求甲同学从终点返回到与乙同学相遇过程中,甲同学距出发地的路程y与x之间的函数关系式.(2)、若甲同学与乙同学相遇后,改由甲同学运球,两人仍以甲第一次到达终点前的速度一起前往终点,则两人到达终点的时间为 秒.18. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.x
…
1
2
4
5
6
8
9
…
y
…
3.92
1.95
0.98
0.78
2.44
2.44
0.78
…
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
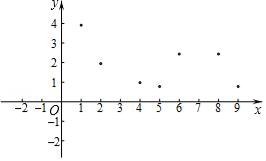
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
 19. 某商品的进价是每件元,原售价每件元,进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:
19. 某商品的进价是每件元,原售价每件元,进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:售价元件
利润元
已知:利润售价进价销售量
(1)、当售价为每件元时,求当天售出多少件商品;
(2)、通过分析表格数据发现,该商品售价每件涨价元时,销售量减少件,设该商品上涨元,销售量为件,用所学过的函数知识求出与之间满足的函数表达式;
(3)、因当地物价局规定,该商品的售价不能超过进价的 , 请求出该商品利润与之间的函数关系式,并计算售价为多少元时,该商品获得最大利润.四、综合题
-
20. 为推进乡村振兴发展,某区决定对A、B两村之间的公路进行改造,并由甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图像所提供的信息解答下列问题:
 (1)、乙工程队每天修公路米.(2)、分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.(3)、若该项工程由甲、乙两工程队一直合作施工,需几天完成?21. 如图,在平面直角坐标系中,菱形的边在轴上,点坐标 , 点在轴正半轴上,且 , 点从原点出发,以每秒一个单位长度的速度沿轴正方向移动,移动时间为秒,过点作平行于轴的直线 , 直线扫过四边形的面积为 .
(1)、乙工程队每天修公路米.(2)、分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.(3)、若该项工程由甲、乙两工程队一直合作施工,需几天完成?21. 如图,在平面直角坐标系中,菱形的边在轴上,点坐标 , 点在轴正半轴上,且 , 点从原点出发,以每秒一个单位长度的速度沿轴正方向移动,移动时间为秒,过点作平行于轴的直线 , 直线扫过四边形的面积为 .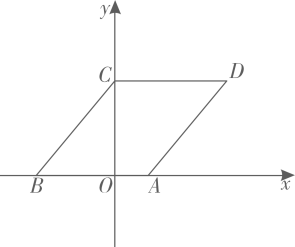 (1)、求点坐标.(2)、求关于的函数关系式.(3)、在直线移动过程中,上是否存在一点 , 使以、、为顶点的三角形是等腰直角三角形?若存在,直接写出点的坐标;若不存在,请说明理由.22. 在平面直角坐标系xOy中,已知点 , , 函数 .
(1)、求点坐标.(2)、求关于的函数关系式.(3)、在直线移动过程中,上是否存在一点 , 使以、、为顶点的三角形是等腰直角三角形?若存在,直接写出点的坐标;若不存在,请说明理由.22. 在平面直角坐标系xOy中,已知点 , , 函数 . (1)、当函数的图象经过点Q时,求m的值并画出直线y=-x-m.(2)、若P,Q两点中恰有一个点的坐标(x,y)满足不等式组(m<0),求m的取值范围.23. 数学活动课上,张老师引导同学进行如下探究:
(1)、当函数的图象经过点Q时,求m的值并画出直线y=-x-m.(2)、若P,Q两点中恰有一个点的坐标(x,y)满足不等式组(m<0),求m的取值范围.23. 数学活动课上,张老师引导同学进行如下探究:如图①,将长为的铅笔斜靠在垂直于水平桌面的直尺的边沿上,一端固定在桌面上,图②是示意图.
如图③,将铅笔绕端点顺时针旋转,与交于点 , 当旋转至水平位置时,铅笔的中点与点重合.
设 , 点到的距离 .
数学思考: (1)、当 , 求点到的距离;(2)、则分别求出和的长(用含的代数式表示);(3)、求出与的函数关系式,并求出自变量的取值范围
(1)、当 , 求点到的距离;(2)、则分别求出和的长(用含的代数式表示);(3)、求出与的函数关系式,并求出自变量的取值范围