备战2024学年中考数学细点逐一突破真题训练第5章解不等式（组）及不等式应用-在线组卷题库

1. 已知 $a - 1 > 0$ ，则下列结论正确的是（）

A、 $- 1 < - a < a < 1$ B、 $- a < - 1 < 1 < a$ C、 $- a < - 1 < a < 1$ D、 $- 1 < - a < 1 < a$

查看试题解析
2. 已知数轴上的点 $A ， B$ 分别表示数 $a ， b$ ，其中 $- 1 < a < 0$ ， $0 < b < 1$ ．若 $a \times b = c$ ，数 $c$ 在数轴上用点 $C$ 表示，则点 $A ， B ， C$ 在数轴上的位置可能是（）

A、 B、 C、 D、

查看试题解析

3. 解不等式组： ${\begin{array}{l} x > \frac{x + 2}{3} \\ 5 x - 3 < 5 + x \end{array}$ ．

查看试题解析
4. 不等式 $\frac{x + 1}{2} \geq \frac{x}{3}$ 的解集是.

查看试题解析
5. 解不等式组： ${\begin{array}{l} 5 x - 2 < 3 (x + 1) ， \\ \frac{3 x - 2}{3} \geq x + \frac{x - 2}{2} \end{array}$ ．

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x \geq x - 1 \\ \frac{x + 1}{2} > \frac{2 x}{3} \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
7. 已知不等式组 ${\begin{cases} x - a > 2 \\ x + 1 < b \end{cases}$ 的解集是 $- 1 ＜ x ＜ 1$ ，则 $(a + b)^{2023}$ =（）

A、0 B、-1 C、1 D、2023

查看试题解析

8. 若实数 $a$ 使关于 $x$ 的不等式组 ${\begin{array}{l} - 2 < x - 1 < 3 \\ x - a > 0 \end{array}$ 的解集为 $- 1 < x < 4$ ，则实数 $a$ 的取值范围为．

查看试题解析
9. 关于 $x$ 的不等式组 ${\begin{array}{l} x + 5 > 0 \\ x - m \leq 1 \end{array}$ 有3个整数解，则实数 $m$ 的取值范围是．

查看试题解析
10. 若关于x的分式方程 $\frac{x}{x - 1} + 1 = \frac{m}{1 - x}$ 的解为非负数，则m的取值范围是（）

A、 $m \leq 1$ 且 $m \neq - 1$ B、 $m \geq - 1$ 且 $m \neq 1$ C、 $m < 1$ 且 $m \neq - 1$ D、 $m > - 1$ 且 $m \neq 1$

查看试题解析
11. 先化简，再求值： $\frac{a^{2} - 6 a + 9}{a - 2} \div (a + 2 + \frac{5}{2 - a})$ ，其中 $a$ 是使不等式 $\frac{a - 1}{2} \leq 1$ 成立的正整数．

查看试题解析

12. 关于x的一次函数 $y = (2 a + 1) x + a - 2$ ，若y随x的增大而增大，且图象与y轴的交点在原点下方，则实数a的取值范围是.

查看试题解析
13. 某服装店经销A，B两种T恤衫，进价和售价如下表所示：

进价（元/件）
45
60
售价（元/件）
66
90

(1)、第一次进货时，服装店用6000元购进A，B两种T恤衫共120件，全部售完获利多少元？

(2)、受市场因素影响，第二次进货时，A种T恤衫进价每件上涨了5元，B种T恤衫进价每件上涨了10元，但两种T恤衫的售价不变．服装店计划购进A，B两种T恤衫共150件，且B种T恤衫的购进量不超过A种T恤衫购进量的2倍．设此次购进A种T恤衫m件，两种T恤衫全部售完可获利W元．
①请求出W与m的函数关系式；
②服装店第二次获利能否超过第一次获利？请说明理由．

查看试题解析
14. 定义：平面直角坐标系 $x O y$ 中，点 $P (a ， b)$ ，点 $Q (c ， d)$ ，若 $c = k a$ ， $d = - k b$ ，其中 $k$ 为常数，且 $k \neq 0$ ，则称点 $Q$ 是点 $P$ 的“ $k$ 级变换点”．例如，点 $(- 4 ， 6)$ 是点 $(2 ， 3)$ 的“ $- 2$ 级变换点”．

(1)、函数 $y = - \frac{4}{x}$ 的图象上是否存在点 $(1 ， 2)$ 的“ $k$ 级变换点”?若存在，求出 $k$ 的值；若不存在，说明理由；

(2)、点 $A (t ， \frac{1}{2} t - 2)$ 与其“ $k$ 级变换点” $B$ 分别在直线 $l_{1}$ ， $l_{2}$ 上，在 $l_{1}$ ， $l_{2}$ 上分别取点 $(m^{2} ， y_{1})$ ， $(m^{2} ， y_{2})$ ．若 $k \leq - 2$ ，求证： $y_{1} - y_{2} \geq 2$ ；

(3)、关于x的二次函数 $y = n x^{2} - 4 n x - 5 n (x \geq 0)$ 的图象上恰有两个点，这两个点的“1级变换点”都在直线 $y = - x + 5$ 上，求n的取值范围．

查看试题解析
15. 已知一次函数 $y = x - k$ ，若对于 $x < 3$ 范围内任意自变量 $x$ 的值，其对应的函数值 $y$ 都小于 $2 k$ ，则 $k$ 的取值范围是．

查看试题解析
16. 抛物线 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $c < 0$ ）经过 $(1 ， 1) ， (m ， 0) ， (n ， 0)$ 三点，且 $n \geq 3$ ．下列四个结论：
① $b < 0$ ；

② $4 a c - b^{2} < 4 a$ ；

③当 $n = 3$ 时，若点 $(2 ， t)$ 在该抛物线上，则 $t > 1$ ；

④若关于 $x$ 的一元二次方程 $a x^{2} + b x + c = x$ 有两个相等的实数根，则 $0 < m \leq \frac{1}{3}$ ．

其中正确的是（填写序号）．

查看试题解析
17. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x (a \neq 0)$ ，满足 ${\begin{array}{l} 3 a + b > 0 \\ a + b < 0 \end{array}$ ，已知点 $(- 3 ， m)$ ， $(2 ， n)$ ， $(4 ， t)$ 在该抛物线上，则m，n，t的大小关系为（）

A、 $t < n < m$ B、 $m < t < n$ C、 $n < t < m$ D、 $n < m < t$

查看试题解析

18. 学校通过劳动教育促进学生树德、增智、强体、育美全面发展，计划组织八年级学生到“开心”农场开展劳动实践活动

.

到达农场后分组进行劳动，若每位老师带

38

名学生，则还剩

6

名学生没老师带；若每位老师带

40

名学生，则有一位老师少带

6

名学生

.

劳动实践结束后，学校在租车总费用

2300

元的限额内，租用汽车送师生返校，每辆车上至少要有

1

名老师

.

现有甲、乙两种大型客车，它们的载客量和租金如表所示：

	甲型客车	乙型客车
载客量 $/ ($ 人 $/$ 辆 $)$	$45$	$30$
租金 $/ ($ 元 $/$ 辆 $)$	$400$	$280$

(1)、参加本次实践活动的老师和学生各有多少名？

(2)、租车返校时，既要保证所有师生都有车坐，又要保证每辆车上至少有

1

名老师，则共需租车辆；

(3)、学校共有几种租车方案？最少租车费用是多少？

查看试题解析

19. 端午节是我国传统节日，端午节前夕，某商家出售粽子的标价比成本高25%，当粽子降价出售时，为了不亏本，降价幅度最多为（）

A、 $20 %$ B、 $25 %$ C、 $75 %$ D、 $80 %$

查看试题解析
20. 金师傅近期准备换车，看中了价格相同的两款国产车．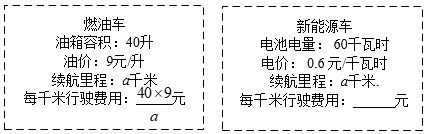

(1)、用含a的代数式表示新能源车的每千米行驶费用．

(2)、若燃油车的每千米行驶费用比新能源车多0.54元．
①分别求出这两款车的每千米行驶费用．

②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

查看试题解析

21. 李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：
品名
甲蔬菜
乙蔬菜
批发价/（元/kg）
          $4.8$
          $4$
零售价/（元/kg）
          $7.2$
          $5.6$

(1)、若他批发甲、乙两种蔬菜共 $40 k g$ 花 $180$ 元．求批发甲乙两种蔬菜各多少千克？（列方程或方程组求解）

(2)、若他批发甲、乙两种蔬菜共 $80 k g$ 花m元，设批发甲种蔬菜 $n k g$ ，求m与n的函数关系式；

(3)、在（2）的条件下，全部卖完蔬菜后要保证利润不低于 $176$ 元，至少批发甲种蔬菜多少千克？

查看试题解析
22. “广安盐皮蛋”是小平故里的名优特产，某超市销售 $A 、 B$ 两种品牌的盐皮蛋，若购买9箱 $A$ 种盐皮蛋和6箱 $B$ 种盐皮蛋共需390元；若购买5箱 $A$ 种盐皮蛋和8箱 $B$ 种盐皮蛋共需310元．

(1)、 $A$ 种盐皮蛋、 $B$ 种盐皮蛋每箱价格分别是多少元？

(2)、若某公司购买 $A 、 B$ 两种盐皮蛋共30箱，且 $A$ 种的数量至少比 $B$ 种的数量多5箱，又不超过 $B$ 种的2倍，怎样购买才能使总费用最少？并求出最少费用．

查看试题解析
23. 为提升学生身体素质，落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神．某校利用课后服务时间，在八年级开展“体育赋能，助力成长”班级篮球赛，共 $16$ 个班级参加．

(1)、比赛积分规定：每场比赛都要分出胜负，胜一场积 $3$ 分，负一场积 $1$ 分．某班级在 $15$ 场比赛中获得总积分为 $41$ 分，问该班级胜负场数分别是多少？

(2)、投篮得分规则：在 $3$ 分线外投篮，投中一球可得 $3$ 分，在 $3$ 分线内 $($ 含 $3$ 分线 $)$ 投篮，投中一球可得 $2$ 分，某班级在其中一场比赛中，共投中 $26$ 个球 $($ 只有 $2$ 分球和 $3$ 分球 $)$ ，所得总分不少于 $56$ 分，问该班级这场比赛中至少投中了多少个 $3$ 分球？

查看试题解析
24. 某商场欲购进A和B两种家电，已知B种家电的进价比A种家电的进价每件多100元，经计算，用1万元购进A种家电的件数与用1.2万元购进B种家电的件数相同．请解答下列问题：

(1)、这两种家电每件的进价分别是多少元？

(2)、若该商场欲购进两种家电共100件，总金额不超过53500元，且A种家电不超过67件，则该商场有哪几种购买方案？

(3)、在（2）的条件下，若A和B两种家电的售价分别是每件600元和750元，该商场从这100件中拿出两种家电共10件奖励优秀员工，其余家电全部售出后仍获利5050元，请直接写出这10件家电中B种家电的件数．

查看试题解析
25. 某健身器材专卖店推出两种优惠活动，并规定购物时只能选择其中一种．
活动一：所购商品按原价打八折；
活动二：所购商品按原价每满300元减80元．（如：所购商品原价为300元，可减80元，需付款220元；所购商品原价为770元，可减160元，需付款610元）

(1)、购买一件原价为450元的健身器材时，选择哪种活动更合算？请说明理由．

(2)、购买一件原价在500元以下的健身器材时，若选择活动一和选择活动二的付款金额相等，求一件这种健身器材的原价．

(3)、购买一件原价在900元以下的健身器材时，原价在什么范围内，选择活动二比选择活动一更合算？设一件这种健身器材的原价为a元，请直接写出a的取值范围．

查看试题解析

备战2024学年中考数学细点逐一突破真题训练第5章解不等式（组）及不等式应用

一、不等式性质

二、不等式（组）及其解集

三、不等式（组）的特殊解

四、函数与不等式结合

五、一次不等式的实际应用

六、方程组与不等式结合

品名	甲蔬菜	乙蔬菜
批发价/（元/kg）	$4.8$	$4$
零售价/（元/kg）	$7.2$	$5.6$


进价（元/件）	45	60
售价（元/件）	66	90