浙江省宁波市海曙区部分校2023-2024学年八年级(上)数学期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(共10小题,每小题3分,共计30分)
-
1. 第19届杭州亚运会刚刚落下帷幕,在如图给出的运动图片中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组长度的三条线段能组成三角形的是( )A、1,2,3 B、1,1,2 C、1,2,2 D、1,5,73. 下列选项中,可以用来证明命题“若|a﹣1|>1,则a>2”是假命题的反例是( )A、a=2 B、a=1 C、a=0 D、a=﹣14. 下列用数轴表示不等式组 的解集正确的是( )A、
2. 下列各组长度的三条线段能组成三角形的是( )A、1,2,3 B、1,1,2 C、1,2,2 D、1,5,73. 下列选项中,可以用来证明命题“若|a﹣1|>1,则a>2”是假命题的反例是( )A、a=2 B、a=1 C、a=0 D、a=﹣14. 下列用数轴表示不等式组 的解集正确的是( )A、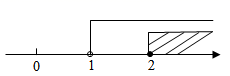 B、
B、 C、
C、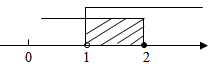 D、
D、 5. 用三角板作 的边BC上的高,下列三角板的摆放位置正确的是( )A、
5. 用三角板作 的边BC上的高,下列三角板的摆放位置正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,直线a∥b , 点A和点B分别在直线a和b上,点C在直线a、b之间,且BC=AC , ∠ACB=120°,∠1=45°,则∠2的度数是( )
6. 如图,直线a∥b , 点A和点B分别在直线a和b上,点C在直线a、b之间,且BC=AC , ∠ACB=120°,∠1=45°,则∠2的度数是( ) A、60° B、65° C、70° D、75°7. 若关于x的不等式(1﹣a)x>3的解集为 , 则a的取值范围是( )A、a<1 B、a>1 C、a≠1 D、a<﹣18. 如图,在△ABC中,AB=AC , BC=6,△ABC的面积是24,AB的垂直平分线ED分别交AC , AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为( )
A、60° B、65° C、70° D、75°7. 若关于x的不等式(1﹣a)x>3的解集为 , 则a的取值范围是( )A、a<1 B、a>1 C、a≠1 D、a<﹣18. 如图,在△ABC中,AB=AC , BC=6,△ABC的面积是24,AB的垂直平分线ED分别交AC , AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为( ) A、7 B、9 C、11 D、149. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( )
A、7 B、9 C、11 D、149. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( ) A、4 B、3 C、2 D、110. 如图,在四边形ABCD中,DA⊥AB . DA=6cm , ∠B+∠C=150°,CD与BA的延长线交于E点,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是( )
A、4 B、3 C、2 D、110. 如图,在四边形ABCD中,DA⊥AB . DA=6cm , ∠B+∠C=150°,CD与BA的延长线交于E点,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是( ) A、12 B、15 C、16 D、18
A、12 B、15 C、16 D、18二、填空题(共6小题,每小题4分,共计24分)
-
11. 把命题“同位角相等”改写成“如果…那么…”的形式为12. 已知等腰三角形的周长为20,其中一边的长为6,则底边的长为 .13. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA , OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE , 点D、E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是 .
 14. 已知:如图所示,在△ABC中,点D、E、F分别为BC、AD、CE的中点,且 , 则阴影部分的面积为cm2 .
14. 已知:如图所示,在△ABC中,点D、E、F分别为BC、AD、CE的中点,且 , 则阴影部分的面积为cm2 . 15. 如图,在Rt△ABC中,∠ACB=90°,BC=40cm,AC=30cm , 动点P从点B出发沿射线BA以2cm/s的速度运动.则当运动时间t=s时,△BPC为直角三角形.
15. 如图,在Rt△ABC中,∠ACB=90°,BC=40cm,AC=30cm , 动点P从点B出发沿射线BA以2cm/s的速度运动.则当运动时间t=s时,△BPC为直角三角形. 16. 如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b , 连接AE , BE,若△ADE与△BEH的面积相等,则= .
16. 如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b , 连接AE , BE,若△ADE与△BEH的面积相等,则= .
三、解答题(共7小题,满分66分)
-
17. 解不等式(组):(1)、2x﹣3(x+1)≥1;(2)、 , 并求出它的所有数解的和.18. 图1,图2,图3均是边长为1的正方形网格,点A , B均在格点上.请只用无刻度的直尺按下列要求在网格中作图(保留痕迹,不要求写作法).
 (1)、在图1中以线段AB为腰作一个等腰锐角三角形ABC;(2)、在图2中以线段AB为腰作一个等腰钝角三角形ABD;(3)、在图3中以线段AB为边作一个四边形ABEF , 使其为轴对称图形.19. 如图,已知△ABC和△ADE , AB=AD , ∠BAD=∠CAE,∠B=∠D , AD与BC交于点P,点C在DE上.
(1)、在图1中以线段AB为腰作一个等腰锐角三角形ABC;(2)、在图2中以线段AB为腰作一个等腰钝角三角形ABD;(3)、在图3中以线段AB为边作一个四边形ABEF , 使其为轴对称图形.19. 如图,已知△ABC和△ADE , AB=AD , ∠BAD=∠CAE,∠B=∠D , AD与BC交于点P,点C在DE上. (1)、求证:BC=DE;(2)、若∠B=30°,∠APC=70°,求∠CAE的度数.20. 如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM .
(1)、求证:BC=DE;(2)、若∠B=30°,∠APC=70°,求∠CAE的度数.20. 如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM . (1)、求证:EF=;(2)、若EF⊥AC , 求证:AM+DM=CB .21. 好笋知时节,当春乃发生.竹笋是中国传统佳肴,味香质脆,在中国自古被当做“菜中珍品”,宁波地区竹林资源丰富,出产普通毛笋的地方也很多,但称得上精品毛笋——“黄泥拱”的只有在大雷.已知,李先生买10千克普通毛笋的钱等于买6千克精品毛笋的钱,买10千克精品毛笋比6千克普通毛笋贵64元.(1)、普通毛笋和精品毛笋每千克进价多少元?(2)、若李先生计划总共购买20千克毛笋,但总支出不超过180元,则李先生最多可以购买多少千克的精品毛笋?22.
(1)、求证:EF=;(2)、若EF⊥AC , 求证:AM+DM=CB .21. 好笋知时节,当春乃发生.竹笋是中国传统佳肴,味香质脆,在中国自古被当做“菜中珍品”,宁波地区竹林资源丰富,出产普通毛笋的地方也很多,但称得上精品毛笋——“黄泥拱”的只有在大雷.已知,李先生买10千克普通毛笋的钱等于买6千克精品毛笋的钱,买10千克精品毛笋比6千克普通毛笋贵64元.(1)、普通毛笋和精品毛笋每千克进价多少元?(2)、若李先生计划总共购买20千克毛笋,但总支出不超过180元,则李先生最多可以购买多少千克的精品毛笋?22.【概念认识】
如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC , BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
 (1)、【问题解决】
(1)、【问题解决】如图②,在△ABC中,∠A=80°,∠B=45°,若∠B的三分线BD交AC于点D , 求∠BDC的度数;
(2)、如图③,在△ABC中,BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线,且∠BPC=140°,求∠A的度数;(3)、【延伸推广】在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P . 若∠A=m°(m>54),直接写出∠BPC的度数.(用含m的代数式表示)
23. 阅读材料:⑴对于任意两个数a、b的大小比较,有下面的方法:
当a﹣b>0时,一定有a>b;
当a﹣b=0时,一定有a=b;
当a﹣b<0时,一定有a<b .
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
⑵对于比较两个正数a、b的大小时,我们还可以用它们的平方进行比较:
∵a2﹣b2=(a+b)(a﹣b),a+b>0
∴(a2﹣b2)与(a﹣b)的符号相同
当a2﹣b2>0时,a﹣b>0,得a>b
当a2﹣b2=0时,a﹣b=0,得a=b
当a2﹣b2<0时,a﹣b<0,得a<b
解决下列实际问题:
(1)、课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x , 每张B5纸的面积为y,且x>y , 张丽同学的用纸总面积为W1 , 李明同学的用纸总面积为W2 . 回答下列问题:①W1= 用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)、如图1所示,要在燃气管道l上修建一个泵站,分别向A、B两镇供气,已知A、B到l的距离分别是3km、4km(即AC=3km , BE=4km),AB=xkm , 现设计两种方案:
方案一:如图2所示,AP⊥l于点P , 泵站修建在点P处,该方案中管道长度a1=AB+AP .
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P , 泵站修建在店P处,该方案中管道长度a2=AP+BP .
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.