浙江省杭州市十三中教育集团2023-2024学年八年级上学期数学11月期中试卷
试卷更新日期：2023-11-24 类型：期中考试
一、选择题（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项最符合题目要求）
-
1. 在以下节水、节能、回收、绿色食品四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 若a＞b ， 则下列选项中，一定成立的是（ ）A、－2a＜－2b B、a－2＜b＋2 C、2a＜2b D、a＋2＜b＋23. 在△ABC中，∠A：∠B：∠C=1：2：3，则此三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形4. 将一副三角尺按如图所示的方式叠放，则∠的度数为（ ）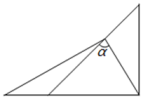
A、45° B、60° C、75° D、15°5. “等腰三角形的两个底角相等”的逆命题是（ ）A、在同一个三角形中，等边对等角 B、两个角互余的三角形是等腰三角形 C、如果一个三角形有两个角相等，那么这个三角形是等腰三角形 D、如果一个三角形有两个底角相等，那么这个三角形是等腰三角形6. 如图，已知AB＝AC ， ∠ADB＝∠E ， 要使△BAD≌△CAE ， 则不符合条件的是（ ）
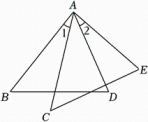A、∠1＝∠2 B、∠B＝∠C C、BD＝CE D、∠BAD＝∠CAE7. 如图，用直尺和圆规作∠MAN的角平分线，根据作图痕迹 ，下列结论不一定正确的是 （ ）
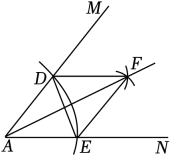A、AD＝AE B、AD＝DF C、DF＝EF D、AF⊥DE8. 已知一个等腰三角形一内角的度数为80°，则这个等腰三角形顶角的度数为（ ）A、20°或80° B、50°或80° C、80° D、100°9. 如图，在四边形ABCD中，AD∥BC ， DE⊥BC ， 垂足为点E ， 连接AC交DE于点F ， 点G为AF的中点，∠ACD＝2∠ACB ． 若DG＝3，EC＝1，则DE的长为（ ）
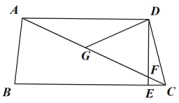A、 B、 C、 D、10. 如图，△AOB≌△ADC ， 点B和点C是对应顶点，∠O＝∠D＝90°，记∠OAD＝α，∠ABO＝β，当BC∥OA时，α与β之间的数量关系为（ ）
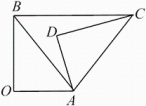A、α＝2β B、α＝β C、α+2β＝180° D、α+β＝90°二、填空题（本大题共6小题，每小题4分，共24分.）
-
11. a与2的和大于0，用不等式表示为 ．12. Rt△ABC中，∠ACB＝90°，AB＝13，AC＝5，则BC的长为 ．13. 已知a、b、c是等腰三角形ABC的三边，a＝3，b＝7，c为整数，△ABC的周长为 ．14. 如图，长方形ABCD中，∠B＝90°，AB＝6，BC＝8，点E是BC边上一点，连接AE ， 把∠B沿AE折叠，使点B落在对角线AC上，则BE的长为 ．
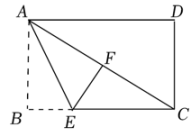15. 如图，直线a ， b交于点O ， ∠α＝60°，点A是直线a上的一个定点，点B在直线b上运动，若以点O ， A ， B为顶点的三角形是等腰三角形，则∠OAB＝°．
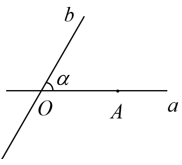16. 如图，在∠AOB的边OA、OB上取点M、N ， 连接MN ， PM平分∠AMN ， PN平分∠MNB ， 若MN＝2，△PMN的面积是2，△OMN的面积是6，则OM＋ON的长是 ．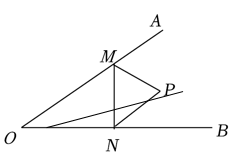
三、解答题（本大题共7小题，共66分.）
-
17. 已知m＜n ， 利用不等式的性质比较2m－1与2n－1的大小．18. 如图，在△ABC中，AB＞AC ．
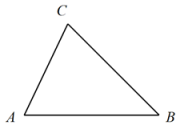(1)、用直尺和圆规作BC的中垂线，交BC于点D ， 交AB于点E（要求保留作图痕迹）；(2)、填空：连接CE ， 若AB=BC ， ∠ECB＝32°，∠A=（直接写出结果）．19. 如图，EF=BC，DF=AC，DA=EB．求证：∠F=∠C．
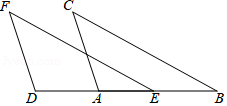20. 如图，在由边长为1个单位的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．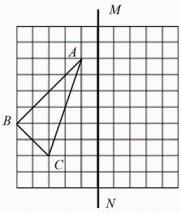
⑴作出△ABC关于直线MN的轴对称图形△A1B1C1；
⑵填空：△A1B1C1的面积为 ▲ （直接写出结果）；
⑶在线段AC上找一点D，使得BD将△ABC分成两个等腰三角形.
21. 国际上广泛使用“身体体重指数（BMI）”作为判断人体健康状况的一个指标：这个指数B等于人体的体重G（kg）除以人体的身高h（m）的平方所得的商，即B＝ ．身体体重指数范围
身体属型
B＜18
不健康瘦弱
18≤B＜20
偏瘦
20≤B＜25
正常
25≤B＜30
超重
B≥30
不健康肥胖
(1)、上表是国内健康组织提供的参考标准，若林老师体重G＝81kg ， 身高h＝1.80m ， 请问他的体型属于哪一种，请说明理由.(2)、赵老师的身高为1.6m ， 那么他的体重在什么范围内时，体型属于正常？22. 如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，F为CE中点，连接DF ， CD＝AE ．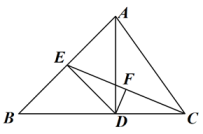
(1)、已知∠BAD＝50°，求∠EDB的度数；(2)、求证：DF⊥CE；(3)、若 ， 求的值．23. 在△ABC中，∠BAC＝90°，AB＝AC ， BC=6，在直线BC上有一点D ， 连结AD ， 以A为直角顶点向AD右侧作等腰直角△ADE ， 连结ED、EC.
(1)、如图1，点D在线段BC上时，求证：△ABD≌△ACE ．(2)、如图2，点D在线段BC延长线上，当EC平分∠AED时，求CD的长．(3)、如图3，点D在线段CB延长线上，AE与BC相交于点F ， 且CF=1，在直线CE上有一点G ， 求AG+FG的最小值.