浙江省杭州市杭州萧山、余杭、富阳、临平多校期中联考2023-2024学年九年级上学期数学11月期中试卷

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题：本题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项最符合题目要求．

1. 在下列四个标志中，是由某个基本图形经过旋转得到的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数y＝(x－1)²－3的最小值是（）

A、2 B、1 C、－2 D、－3

查看试题解析
3. 已知 $⊙ O$ 的半径为3，点 $P$ 在 $⊙ O$ 外，则 $O P$ 的长可能是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 已知二次函数 $y = x^{2} + m x$ 的图象的对称轴为直线 $x = 2$ ，则抛物线 $y = x^{2} + m x$ 在 $x$ 轴上截得的线段长为（）

A、4 B、5 C、6 D、7

查看试题解析
5. 如图，AB是⊙O的直径，点C在圆上，若 $\overset{⌢}{C D}$ ＝64°，则∠CBA的度数为（）

A、32° B、64° C、68° D、58°

查看试题解析
6. 若二次函数y＝－5x²＋px＋q的图象经过A（a ， b），B（0，y₁），C（4－a ， b），D（1，y₂），E（4，y₃），则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＝y₃ C、y₃＝y₁＜y₂ D、y₃＜y₂＜y₁

查看试题解析
7. 一枚质地均匀的正方体骰子，骰子各面分别标有数字1、2、3、4、5、6，掷两次所得点数之和为11的概率为（）

A、 $\frac{1}{18}$ B、 $\frac{1}{36}$ C、 $\frac{1}{12}$ D、 $\frac{1}{15}$

查看试题解析
8. 已知二次函数y＝ax²＋bx＋c（a≠0，a ， b ， c是常数）的部分自变量x与函数y的对应值：
x
－1
$－ \frac{1}{2}$
0
$\frac{1}{2}$
1
$\frac{3}{2}$
2
$\frac{5}{2}$
3
y
－2
$－ \frac{1}{4}$
1
$\frac{7}{4}$
2
$\frac{7}{4}$
1
$－ \frac{1}{4}$
－2
则方程ax²＋bx＋c＝0（a≠0，a ， b ， c是常数）两根x₁ ， x₂的取值范围是（）

A、－ $\frac{1}{2}$ ＜x₁＜0， $\frac{3}{2}$ ＜x₂＜2 B、－1＜x₁＜－ $\frac{1}{2}$ ， 2＜x₂＜ $\frac{5}{2}$ C、－1＜x₁＜－ $\frac{1}{2}$ ， $\frac{3}{2}$ ＜x₂＜2 D、－ $\frac{1}{2}$ ＜x₁＜0，2＜x₂＜ $\frac{5}{2}$

查看试题解析
9. 如图，已知BC是⊙O的直径，半径OA⊥BC ，点D在劣弧 $\overset{⌢}{A C}$ 上（不与点A ，点C重合），BD与OA交于点E ，设∠AED＝α ， ∠AOD＝β ，则（）

A、2α＋β＝180° B、2α－β＝90° C、3α＋β＝180° D、3α－β＝90°

查看试题解析
10. 已知二次函数y＝ax²＋bx＋c（a≠0）的图象如图所示，有下列结论：①abc＞0；②b²＜4ac；③a－b＋c＜0；④a＋b＞m(am＋b)（m≠1）；⑤若方程|ax²＋bx＋c|＝1有四个根，则这四个根的和为2．其中正确的为（）

A、①② B、②④ C、③④ D、②⑤

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

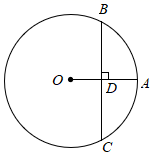
11. 二次函数y＝x²－4x＋3的图象的对称轴是直线．

查看试题解析
12. 如图，点 $A$ 在 $⊙ O$ 上，弦 $B C$ 垂直平分 $O A$ ，垂足为 $D$ ．若 $O A = 4$ ，则 $B C$ 的长为．

查看试题解析
13. 把一枚硬币连续抛掷两次，则两次都正面朝上的概率是．

查看试题解析
14. 如图，将一块含30°角的直角三角板的锐角顶点A放在⊙O上，边AB ， AC分别与⊙O交于点D ， E ．则 $\overset{⌢}{D E}$ 的度数为．

查看试题解析
15. 当a－2≤x≤a＋1时，函数y＝－x²＋2x＋3的最大值为3，则a的值为．

查看试题解析
16. 如图，已知半圆O ， OB＝ $\sqrt{61}$ ．点D在半圆上，AD＝10，在 $\overset{⌢}{B D}$ 取点C ，连结AC ，作DH⊥AC于点H ，连结BH ，则BH的最小值等于．

查看试题解析

三、解答题：本题有8个小题，共66分．

17. 如图，在⊙O中，弦AB、CD的延长线交于点P，且DA＝DP．求证：BC＝BP．

查看试题解析
18. 已知，在平面直角坐标系中，二次函数y＝－x²＋bx＋5的图象经过点M（－4，5）．

(1)、求b的值，并写出此抛物线的对称轴．

(2)、求抛物线与x轴的交点坐标．

查看试题解析
19. 已知非负数a ， b ， c ，且有a＋b＝2，c－3a＝4．设S＝a²＋b＋c ，记S的最大值为m ， S的最小值为n ，求m和n的值．

查看试题解析
20. 如图是两个转盘，每个转盘都被圆的半径三等分，甲转盘的三个扇形上标有数字2，4，6，乙转盘的三个扇形上标有数字1，3，5．小明和小力分别转动甲、乙转盘，每人转动一次，记录转盘停止后指针指向的数字，若指针指在分界线上则重转．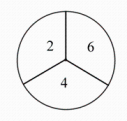

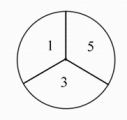(1)、两人分别转动甲、乙转盘后，可能出现的全部可能有哪些？请用列表或画树状图的方法表示．

(2)、若得到的两数字之和是3的倍数，则小明赢；若得到的两数字之和是7的倍数，则小力赢，此游戏公平吗？为什么？

查看试题解析
21. 如图，A ， B ， C是⊙O上三点，且 $\overset{⌢}{A B}$ ＝2 $\overset{⌢}{B C}$ ，过点B作BD⊥OC于点D ．

(1)、求证：AB＝2BD ．

(2)、若AB＝ $2 \sqrt{3}$ ， CD＝1，求⊙O的半径．

查看试题解析
22. 如图是一块篱笆围成的矩形土地ABCD ，并且由一条与CD边平行的篱笆EF分开，已知篱笆的总长为90米（厚度不计）．设AB＝x米，AD＝y米．

(1)、用含有x的代数式表示y ．

(2)、设矩形土地ABCD面积为S平方米，当16≤x≤20时，求S的最大值．

查看试题解析
23. 已知，二次函数y＝x²＋2bx＋b²－2（b＞0）．

(1)、用含b的代数式表示抛物线图象的顶点坐标．

(2)、若这个二次函数的图象经过点B（0，－1），
①当－2＜x＜3，求y的取值范围．
②当k≤x≤2时，－2≤y≤7时，结合函数图象，求出k的取值范围．

查看试题解析
24. 如图，AB是⊙O的直径，弦CD⊥AB与点E ，已知AB＝10，AE＝8，点P为AB上任意一点，（点P不与A、B重合），连结CP并延长与⊙O交于点Q ，连结QD ， PD ， AD ．

(1)、求CD的长．

(2)、若CP＝PQ ，直接写出AP的长．

(3)、①若点P在A ， E之间（点P不与点E重合），求证：∠ADP＝∠ADQ ．
②若点P在B ， E之间（点P不与点E重合），求∠ADP与∠ADQ满足的关系．

查看试题解析

x	－1	$－ \frac{1}{2}$	0	$\frac{1}{2}$	1	$\frac{3}{2}$	2	$\frac{5}{2}$	3
y	－2	$－ \frac{1}{4}$	1	$\frac{7}{4}$	2	$\frac{7}{4}$	1	$－ \frac{1}{4}$	－2