浙江省金华市五校2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、单选题(本题有10小题,每小题3分,共30分)
-
1. 下列图形中是旋转对称图形但不是中心对称图形的是( )A、
 B、
B、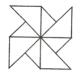 C、
C、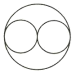 D、
D、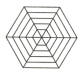 2. 若 , 则=( )A、 B、 C、 D、3. 如图,某天气预报软件显示“义乌市明天的降水概率为85%”对这条信息的下列说法中,正确的是( )A、义乌市明天将有85%的时间下雨 B、义乌市明天将有85%的地区下雨 C、义乌市明天下雨的可能性较大 D、义乌市明天下雨的可能性较小4. 如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么下列结论不一定正确的是( )
2. 若 , 则=( )A、 B、 C、 D、3. 如图,某天气预报软件显示“义乌市明天的降水概率为85%”对这条信息的下列说法中,正确的是( )A、义乌市明天将有85%的时间下雨 B、义乌市明天将有85%的地区下雨 C、义乌市明天下雨的可能性较大 D、义乌市明天下雨的可能性较小4. 如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么下列结论不一定正确的是( ) A、△AOD∽△BOC B、△AOB∽△DOC C、CD=BC D、BC•CD=AC•OA5. 把二次函数的解析式配成顶点式为( )A、 B、 C、 D、6. 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子 , 在点被钉在一起,并使它们保持垂直,在测直径时,把点靠在圆周上,尺子与圆交于点 , 尺子与圆交于点 , 读得为个单位长度,为个单位长度.则圆的直径为( )
A、△AOD∽△BOC B、△AOB∽△DOC C、CD=BC D、BC•CD=AC•OA5. 把二次函数的解析式配成顶点式为( )A、 B、 C、 D、6. 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子 , 在点被钉在一起,并使它们保持垂直,在测直径时,把点靠在圆周上,尺子与圆交于点 , 尺子与圆交于点 , 读得为个单位长度,为个单位长度.则圆的直径为( )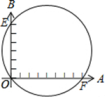 A、个单位长度 B、个单位长度 C、个单位长度 D、个单位长度7. 如图,已知二次函数的图象与轴分别交于两点,与轴交于点, , 则由抛物线的特征写出如下结论中错误的是( )
A、个单位长度 B、个单位长度 C、个单位长度 D、个单位长度7. 如图,已知二次函数的图象与轴分别交于两点,与轴交于点, , 则由抛物线的特征写出如下结论中错误的是( ) A、 B、 C、 D、8. 如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(点C与点A不重合),CF⊥CD交AB于F,DE⊥CD交AB于E,G为半圆中点,当点C在上运动时,设的长为 , CF+DE=y , 则下列图象中,能表示y与的函数关系的图象大致是( )
A、 B、 C、 D、8. 如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O的半径(点C与点A不重合),CF⊥CD交AB于F,DE⊥CD交AB于E,G为半圆中点,当点C在上运动时,设的长为 , CF+DE=y , 则下列图象中,能表示y与的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 已知二次函数y=x2-2x+m的图象C与y轴交于点M,过点M作直线l平行于x轴,将抛物线C位于直线l下方的部分翻折至直线l上方.若变换后的图象与x轴有4个交点,则m的取值范围为( )A、m>—1 B、-1<m<0 C、-1≤m≤0 D、-1≤m<010. 如图△ABC中,∠ACB=90°,AB=4,AC=x , ∠BAC=α,O为AB中点,若点D为直线BC下方一点,且△BCD与△ABC相似,则下列结论:
9. 已知二次函数y=x2-2x+m的图象C与y轴交于点M,过点M作直线l平行于x轴,将抛物线C位于直线l下方的部分翻折至直线l上方.若变换后的图象与x轴有4个交点,则m的取值范围为( )A、m>—1 B、-1<m<0 C、-1≤m≤0 D、-1≤m<010. 如图△ABC中,∠ACB=90°,AB=4,AC=x , ∠BAC=α,O为AB中点,若点D为直线BC下方一点,且△BCD与△ABC相似,则下列结论:
①若α=60°,则AD的最大值为;
②若α=60°,△ABC∽△CBD , 则OD的长为;
③若α=45°,BC与OD相交于E , 则点E不一定是△ABD的重心;
④若△ABC∽△BCD , 则当x=2时,AC+CD取得最大值.其中正确的为( )
A、①③ B、①②④ C、③④ D、①③④二、填空题(本题有6小题,每小题4分,共24分)
-
11. 已知抛物线的解析式为 , 则该抛物线的顶点坐标是 .12. 一个扇形的弧长为 ,面积为 ,则这个扇形的半径是 .13. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.4左右,则袋子中红球的大约有个.14. 如图,要拧开一个边长a=18mm的六角形螺帽,扳手张开的开口b至少要mm..
 15. 关于抛物线 , 与x轴交于A、B两点(A在B左侧),若点P在抛物线上,且满足(a为常数)的点有且只有3个,则a的值为 .16. 如图,在四边形ABCD中,AD∥BC , ∠DAB=30°,∠ADC=60°,BC=CD=3,若线段MN在边AD上运动,且MN=1,则AD的长为 , BM2+2BN2的最小值是.
15. 关于抛物线 , 与x轴交于A、B两点(A在B左侧),若点P在抛物线上,且满足(a为常数)的点有且只有3个,则a的值为 .16. 如图,在四边形ABCD中,AD∥BC , ∠DAB=30°,∠ADC=60°,BC=CD=3,若线段MN在边AD上运动,且MN=1,则AD的长为 , BM2+2BN2的最小值是.
三、解答题解答题(本题有8小题,共66分)
-
17. 如图,点在等边的边上,为等边三角形,与交于点 . 求证: .
 18. 如图①、图②都是的网格,每个小正方形的顶点称为格点.点、均在格点上.图①、图②中的点在上,仅用无刻度的直尺,按下列要求完成画图,所画图形的顶点均在格点上,并保留作图痕迹.
18. 如图①、图②都是的网格,每个小正方形的顶点称为格点.点、均在格点上.图①、图②中的点在上,仅用无刻度的直尺,按下列要求完成画图,所画图形的顶点均在格点上,并保留作图痕迹. (1)、在图①中画一个的内接正方形.(2)、在图②中画一个的内接四边形 , 使该四边形是轴对称图形但不是中心对称图形,且点在该四边形内部.19. 一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.(1)、求第一次摸出的球上的数字为奇数的概率;(2)、请用树状图或列表法求两次摸出的球上的数字之和不小于3的概率.20. 如图,抛物线y=x2+bx-3与x轴交于A , B两点,与y轴交于C点,且A(-1,0).
(1)、在图①中画一个的内接正方形.(2)、在图②中画一个的内接四边形 , 使该四边形是轴对称图形但不是中心对称图形,且点在该四边形内部.19. 一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.(1)、求第一次摸出的球上的数字为奇数的概率;(2)、请用树状图或列表法求两次摸出的球上的数字之和不小于3的概率.20. 如图,抛物线y=x2+bx-3与x轴交于A , B两点,与y轴交于C点,且A(-1,0). (1)、求抛物线的解析式及顶点D的坐标;(2)、点M是对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.21. 如图,在中, , 以点C为圆心,长为半径的圆交于点D.
(1)、求抛物线的解析式及顶点D的坐标;(2)、点M是对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.21. 如图,在中, , 以点C为圆心,长为半径的圆交于点D. (1)、若 , 求的度数;(2)、若D是的中点,且AB=4,求阴影部分(弓形)的面积.22. 小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(且为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:(1)、求p与x的函数关系式;(2)、若每天的销售利润为w元,求w与x的函数关系式;(3)、请你帮小张求出第几天的销售利润最大,最大销售利润是多少元?23. 我们定义:若点P在一次函数y=ax+b(a≠0)图象上,点Q在反比例函数图象上,且满足点P与点Q关于y轴对称,则称二次函数y=ax2+bx+c为一次函数y=ax+b与反比例函数的“衍生函数”,点P称为“基点”,点Q称为“靶点”.(1)、若二次函数y=2x2+6x+8是一次函数y=ax+b与反比例函数的“衍生函数”,则a= , b= , c= .(2)、直接写出一次函数y=x+b和反比例函数的“衍生函数”的表达式,若该“衍生函数”的顶点在x轴上,且“基点”P的横坐标为4,求出“靶点”Q的坐标;(3)、若一次函数y=ax+b(a>b>0)和反比例函数的“衍生函数”经过点(2,5).试判断一次函数y=ax+b图象上“基点”的个数,并说明理由;24. 在平面直角坐标系中,点B、E的坐标分别为B(-2,),E(4,0),过点E作直线l⊥x轴,设直线l上的动点A的坐标为(4,m),连接AB , 将线段BA绕点B顺时针方向旋转30°得到线段BA′,在射线BA′上取点C , 构造Rt△ABC , 使得∠BAC=90°.
(1)、若 , 求的度数;(2)、若D是的中点,且AB=4,求阴影部分(弓形)的面积.22. 小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(且为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:(1)、求p与x的函数关系式;(2)、若每天的销售利润为w元,求w与x的函数关系式;(3)、请你帮小张求出第几天的销售利润最大,最大销售利润是多少元?23. 我们定义:若点P在一次函数y=ax+b(a≠0)图象上,点Q在反比例函数图象上,且满足点P与点Q关于y轴对称,则称二次函数y=ax2+bx+c为一次函数y=ax+b与反比例函数的“衍生函数”,点P称为“基点”,点Q称为“靶点”.(1)、若二次函数y=2x2+6x+8是一次函数y=ax+b与反比例函数的“衍生函数”,则a= , b= , c= .(2)、直接写出一次函数y=x+b和反比例函数的“衍生函数”的表达式,若该“衍生函数”的顶点在x轴上,且“基点”P的横坐标为4,求出“靶点”Q的坐标;(3)、若一次函数y=ax+b(a>b>0)和反比例函数的“衍生函数”经过点(2,5).试判断一次函数y=ax+b图象上“基点”的个数,并说明理由;24. 在平面直角坐标系中,点B、E的坐标分别为B(-2,),E(4,0),过点E作直线l⊥x轴,设直线l上的动点A的坐标为(4,m),连接AB , 将线段BA绕点B顺时针方向旋转30°得到线段BA′,在射线BA′上取点C , 构造Rt△ABC , 使得∠BAC=90°. (1)、如图1,当m=-时,求直线AB的函数表达式.(2)、当点C落在x轴上如图2的位置时,求点C的坐标.(3)、已知点B关于原点O的对称点是点D , 在点A的运动过程中,是否存在某一位置,使△ACD与△ABC相似(包括全等)?若存在,请直接写出点A的坐标;若不存在,请说明理由.
(1)、如图1,当m=-时,求直线AB的函数表达式.(2)、当点C落在x轴上如图2的位置时,求点C的坐标.(3)、已知点B关于原点O的对称点是点D , 在点A的运动过程中,是否存在某一位置,使△ACD与△ABC相似(包括全等)?若存在,请直接写出点A的坐标;若不存在,请说明理由.