浙江省嘉兴市平湖区六校联考2023-2024学年九年级上学期数学期中试卷
试卷更新日期：2023-11-24 类型：期中考试
一、选择题（本大题有10小题，每小题3分，共30分）
-
1. 下列事件是必然事件的是（ ）A、明天会下雨 B、抛一枚硬币，正面朝上 C、若a是实数，则|a|≥0 D、打开电视，正在播放新闻2. 抛物线y＝-2（x+3）2+4的顶点坐标是（ ）A、（3，4） B、（-3，4） C、（3，-4） D、（-3，-4）3. 若⊙O的半径是3，点P在圆外，则点OP的长可能是（ ）A、1 B、2 C、3 D、64. 如图，点 、 、 在 上，若 ，则 的度数是（ ）
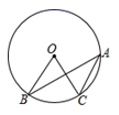A、18° B、36° C、54° D、72°5. 若点A（4，y1），B（2，y2），C（-2，y3）是抛物线y＝（x-2）2+1上的三点，则y1 ， y2 ， y3的大小关系为（ ）A、y3＞y1＞y2 B、y1＞y3＞y2 C、y3＞y2＞y1 D、y1＞y2＞y36. 如图，四边形ABCD内接于 ， 若 ， 则的度数为（ ）
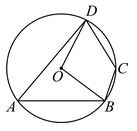A、50° B、100° C、130° D、150°7. 已知抛物线y＝x2+mx+9的顶点在x轴上，则m的值为（ ）A、6 B、±6 C、±3 D、±98. 如图，△ABC中，∠ACB＝36°，AC＝BC ， 将△ABC绕点A旋转到△ADE处，使DE恰好过点B ， 则∠E等于（ ）
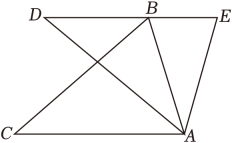A、72° B、60° C、36° D、30°9. 如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A ， B两点，与y轴正半轴交于点C ， 它的对称轴为直线x＝-1．则下列选项中正确的是（ ）
A、abc＜0 B、4ac-b2＞0 C、c-a＞0 D、2a-b＝010. 已知二次函数y＝ax2-（3a+1）x+3（a≠0），下列说法正确的是（ ）A、点（1，2）在该函数的图象上 B、当a＝1且-1≤x≤3时，0≤y≤8 C、该函数的图象与x轴一定有交点 D、当a＞0时，该函数图象的对称轴一定在直线x＝的左侧二、填空题（本大题有6小题，每小题3分，共18分）
-
11. 某班共有学生36人，在迎新年庆祝会上，随机抽取1名一等奖，3名二等奖，5名三等奖，以上统称为等第奖，该班每一名学生获得等第奖的概率是 ．12. 在平面直角坐标系中，将抛物线y=（x﹣1）2先向上平移2个单位长度，再向右平移3个单位长度，得到的抛物线的解析式是 ．13. 汽车刹车后行驶的距离s（单位：m）关于行驶的时间（单位：）的函数解析式是s＝15t-6t2 ， 汽车刹车后到停下来前进了米．14. 如图，在平面直角坐标系xOy中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0），那么△ABC的外接圆的圆心坐标为.
15. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A ， B ， C ， D分别是“果圆”与坐标轴的交点，抛物线的表达式为y＝x2-2x-6，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为 ．
16. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为 ．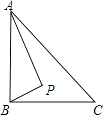
三、解答题（本大题有8小题，第17～22题每题6分，第23、24题每题8分，共52分）
-
17. 已知抛物线y＝a（x-h）2的对称轴是直线x＝-2，且过点（1，-3）．(1)、求这个二次函数的表达式；(2)、x在什么范围内，y随x增大而减小？该函数有最大值还是有最小值？求出这个最值．18. 一个不透明的口袋中有三个完全相同的小球，球上分别标有数字-1，1，2．第一次从袋中任意摸出一个小球（不放回），得到的数字作为点M的横坐标x；再从袋中余下的两个小球中任意摸出一个小球，得到的数字作为点M的纵坐标y ．(1)、用列表法或画树状图法，列出点M（x ， y）的所有可能结果；(2)、求点M（x ， y）在反比例函数y＝的图象上的概率．19. 如图，△AOB的三个顶点都在网格的格点上，网格中的每个小正方形的边长均为一个长度单位，以点O建立平面直角坐标系．
(1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1；(2)、写出点A1 ， B1的坐标．20. 如图，A是⊙O上一点，BC是直径，点D在⊙O上且平分 ．
(1)、连接AD ， 求证：AD平分∠BAC；(2)、若 ， AB＝8，求AC的长．21. 小红经营的网店以销售文具为主，其中一款笔记本进价为每本10元，该网店在试销售期间发现，每周销售数量y（本）与销售单价x（元）之间满足一次函数关系，三对对应值如下表：销售单价x（元）
12
14
16
每周的销售量y（本）
500
400
300
(1)、求y与x之间的函数关系式；(2)、通过与其他网店对比，小红将这款笔记本的单价定为x元（12≤x≤15，且x为整数），设每周销售该款笔记本所获利润为w元，当销售单价定为多少元时每周所获利润最大，最大利润是多少元？22. 如图，在平面直角坐标系中，△CBO的外接圆⊙M与y轴交于点A（0，），∠C＝60°，∠COB＝45°．
(1)、求OB的长．(2)、求OC的长．23. 根据素材解决问题．
设计货船通过圆形拱桥的方案
素材1
图1中有一座圆拱石桥，图2是其圆形桥拱的示意图，测得水面宽AB＝16m ， 拱顶离水面的距离CD＝4m ．
素材2
如图3，一艘货船露出水面部分的横截面为矩形EFGH ， 测得EF＝3m ， EH＝10m ． 因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度y（米）与货船增加的载重量x（吨）满足函数关系式 ．
问题解决
(1)、任务1：确定桥拱半径求圆形桥拱的半径
(2)、任务2：拟定设计方案根据图3状态，货船能否通过圆形拱桥？若能，最多还能卸载多少吨货物？若不能，至少要增加多少吨货物才能通过？
24. 如图，直线y＝-x+3交y轴于点A ， 交x轴于点C ， 抛物线y＝-+bx+c经过点A ， 点C ， 且交x轴于另一点B ．
(1)、直接写出点A ， 点B ， 点C的坐标及抛物线的解析式；(2)、在直线AC上方的抛物线上有一点M ， 求四边形ABCM面积的最大值及此时点M的坐标；(3)、将线段OA绕x轴上的动点P（m ， 0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．