浙江省台州市临海市第六教研区2023-2024学年八年级上学期数学期中检测试卷
试卷更新日期：2023-11-24 类型：期中考试
一、选择题（本大题共10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
-
1. 第19届亚运会于2023年9月在杭州举行，下列历届亚运会会徽是轴对称图形的是（ ）A、
B、
C、
D、
2. 在△ABC中，作出AC边上的高，正确的是（ ）.A、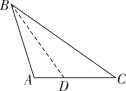
B、
C、
D、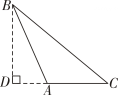
3. 我校某班级计划在学校耕读园里搭三角形围栏，可以选择以下三种长度的木条组合的是（ ）A、3、4、8 B、4、4、8 C、3、5、6 D、5、6、114. 下图中显示的是从镜子中看到的背后墙上电子钟的读数，由此你可以推断这时的实际时间是（ ）
A、10：05 B、20：01 C、20：10 D、10：025. 用直尺和圆规作一个角等于已知角，如图所示，能得出△OCD≌△O'C'D'的依据是（ ）
A、SSS B、SAS C、ASA D、AAS6. 等腰三角形的周长是8cm，其中一边长为2cm，则该等腰三角形的底边长为（ ）A、2cm B、3cm C、4cm D、2cm或4cm7. 如图所示，△ABC与△DEF关于直线l对称，下列说法错误的是（ ）
A、AB＝DE B、∠BAC＝∠EDF C、点B和点E到直线l的距离相等 D、AC//DE8. 如图1是一个平板电脑支架，由托板、支撑板和底座构成，平板电脑放置在托板上，图2是其侧面结构示意图．现量得托板长AB＝10cm，支撑板顶端的C恰好是托板AB的中点，托板AB可绕点C转动，支撑板CD可绕点D转动．当CD⊥AB ， 且射线DB恰好是∠CDE的平分线时，此时点B到直线DE的距离是（ ）
A、5cm B、6cm C、8cm D、10cm9. 如图，点A ， B是4×4网格中的格点，网格中的每个小正方形的边长为1，如果以A ， B ， C为顶点的三角形是等腰三角形，则满足条件的所有格点C有（ ）个．
A、6 B、7 C、8 D、910. 如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE ． 如果∠A=α，∠DEA=β，∠CEA'=γ，∠BDA'=θ，那么下列式子中不一定成立的是（ ）
A、θ=2α+γ B、θ=180°﹣α﹣γ C、β= D、θ=2α+2β﹣180°二、填空题（本题共6小题，每小题4分，共24分）
-
11. 某校拍摄秋季运动会比赛盛况的摄影机架是三角形，这是利用了 ．12. 点（2023，-2024）关于x轴对称的点的坐标为 ．13. 如图，要测量池塘两岸相对的两点A ， B的距离，可以在池塘外取AB的垂线BF上的两点C ， D ， 使BC＝CD ， 再画出BF的垂线DE ， 使E与A ， C在一条直线上．若想知道两点A ， B的距离，只需要测量出线段的长度即可．
14. 如图，将长方形纸片进行折叠，ED ， EF为折痕，A与A＇，B与B＇，C与C＇重合，且B＇在A＇E上，若∠AED=25°，则∠BEF的度数为 ．
15. 如图，△ABC中，AD是△ABC的角平分线，BE是△ABD边AD上的中线，若△ABC的面积是30，AB=9，AC=6，则△ABE的面积是 ．
16. 在平面直角坐标系中，点A（0，4），B（2，0），在平面内有一点C（不与点B重合），使得△AOC与△AOB全等，则点C的坐标可以为 ．
三、解答题（本题共8小题，第17-19题每小题6分，第20-21题每小题8分，第22-23题每小题10分，第24题12分，共66分）
-
17. 如图，校园有两条路OA和OB ， 旁边有两块指示牌C ， D ， 学校准备在附近安装一盏路灯，要求灯柱的位置P离两块指示牌一样远，并且到两条路的距离相等，请你帮助画出灯柱的位置P（要求尺规作图并保留作图痕迹）．
18. 在棋盘中建立如图的直角坐标系，三颗棋子A ， O ， B的位置如图1，它们分别是（-1，1），（0，0）和（1，0）．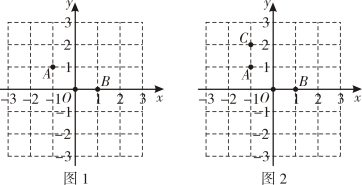
(1)、如图2，添加棋子C ， 使A ， O ， B ， C四颗棋子组成一个轴对称图形，请在图中画出该图形的对称轴；(2)、要在其他格点位置添加一颗棋子P ， 使A ， O ， B ， P四颗棋子组成一个轴对称图形，请直接写出棋子P的所有可能位置的坐标．19. 如图，把一个长为10m的梯子AB斜靠在墙上，测得AM＝8m，BM＝6m，梯子沿墙下滑到CD位置，测得∠ABM＝∠DCM ， 求梯子下滑的高度AC ．
20. 如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，下图是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．
(1)、将下面的表格补充完整：正多边形的边数
3
4
5
6
……
n
∠α的度数
60°
……
(2)、根据规律，是否存在一个正n边形，使其中的∠α＝16°？若存在，直接写出n的值；若不存在，请说明理由．21. 如图，在△ABC中，AB边的垂直平分线l1交BC于点D ， AC边的垂直平分线l2交BC于点E ， l1与l2相交于点O ． 已知△ADE的周长为8cm．
(1)、求BC的长；(2)、分别连接OA ， OB ， OC ， 若△OBC的周长为20cm，求OA的长．22. 如图，在△ABC中，∠ACB=90°，AC=BC ， BE⊥CE于点E ， AD⊥CE于点D ．
(1)、求证：△ADC≌△CEB ．(2)、若AD=5cm，DE=3cm，求BE的长度．23. 已知△ABC ．
(1)、如图1，若三角形的内角∠ABC与∠ACB的平分线交于点O ， 求证：①∠BOC=；
②∠BOC=；
(2)、如图2，若三角形的外角∠DBC与∠ECB的平分线交于点O ， 试分析∠BOC与∠A有怎样的数量关系，请说明理由；(3)、如图3，若三角形的内角∠ABC与外角∠ACD的平分线交于点O ， 则∠BOC与∠A的数量关系为 ． (只写结论，不需证明)24.
(1)、某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ， 直线l经过点A ， BD⊥直线l ， CE⊥直线l ， 垂足分别为点D、E ． 证明：DE＝BD+CE ．(2)、组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ， 其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ， 求证：I是EG的中点．