浙江省宁波市海曙区宁波市海曙区十校联考2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 若 , 则的值等于( ).A、 B、 C、 D、52. 下列事件中是必然事件的是( )A、拔苗助长 B、瓮中捉鳖 C、海底捞月 D、守株待兔3. 如图,能使成立的条件是( )
 A、 B、 C、 D、4. 由二次函数 , 可知下列说法正确的是( )A、其最小值为1 B、其图像的对称轴为直线 C、当时,随的增大而增大 D、其图像与轴的交点为5. 下列说法正确的是( )A、平分弦的直径垂直于弦 B、不在同一直线上的三点确定一个圆 C、直径是弦,弦是直径 D、长度相等的弧是等弧6. 如图,在中, , 则的度数为( )
A、 B、 C、 D、4. 由二次函数 , 可知下列说法正确的是( )A、其最小值为1 B、其图像的对称轴为直线 C、当时,随的增大而增大 D、其图像与轴的交点为5. 下列说法正确的是( )A、平分弦的直径垂直于弦 B、不在同一直线上的三点确定一个圆 C、直径是弦,弦是直径 D、长度相等的弧是等弧6. 如图,在中, , 则的度数为( ) A、 B、 C、 D、7. 如图,是的直径,弦于 , 若 , , 则直径的长为( )
A、 B、 C、 D、7. 如图,是的直径,弦于 , 若 , , 则直径的长为( ) A、10 B、12 C、15 D、208. 如图,在正方形中,为线段上一点且 , 连结 , 交于点 , 分别作 , 的中点M , N , 连结 , 若 , 则为( )
A、10 B、12 C、15 D、208. 如图,在正方形中,为线段上一点且 , 连结 , 交于点 , 分别作 , 的中点M , N , 连结 , 若 , 则为( )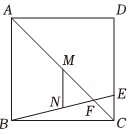 A、1 B、 C、2 D、9. 如图,二次函数的图象过点 , 对称轴为直线 , 下列结论:①;②;③;④当时,的取值范围是;其中正确的个数为( )
A、1 B、 C、2 D、9. 如图,二次函数的图象过点 , 对称轴为直线 , 下列结论:①;②;③;④当时,的取值范围是;其中正确的个数为( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本题有6小题,每小题4分,共24分)
-
10. 一道你完全不会的数学选择题,你做对的概率为.11. 把抛物线先向左平移1个单位,再向上平移3个单位,则平移后的抛物线表达式为.12. 如图,在平行四边形中,是线段上一点,连结、交于点.若 , 则.
 13. 如图,在半径为2的扇形中, , 将扇形沿过点B的直线折叠,点O恰好落在弧上,折痕交于点C , 则图中阴影部分的周长是.
13. 如图,在半径为2的扇形中, , 将扇形沿过点B的直线折叠,点O恰好落在弧上,折痕交于点C , 则图中阴影部分的周长是. 14. 点 , 都在二次函数的图象上.若 , 则的取值范围为.15. 如图,是的直径,为圆上一点,连结 , D , E分别为 , 的中点, , 若为弧上的三等分点,且靠近点,连结 , 则的最小值为.
14. 点 , 都在二次函数的图象上.若 , 则的取值范围为.15. 如图,是的直径,为圆上一点,连结 , D , E分别为 , 的中点, , 若为弧上的三等分点,且靠近点,连结 , 则的最小值为.
三、解答题(本大题共8小题,共66分.)
-
16. 一个不透明的袋中装有分别标着汉字“杭”、“州”、“亚”、“运”的四个小球,除标注的汉字不同外,小球无任何区别,每次摸球前先搅拌均匀再摸球。(1)、从袋中摸出一个球,球上的汉字刚好是“杭”的概率是.(2)、从袋中任摸一球,不放回,再从袋中任摸一球,请用树状图(或列表法)表示出所有可能出现的结果,并求出摸到的两个球上的汉字恰好能组成“亚运”的概率。17. 如图,在正方形网格中,每个小正方形边长为1,当三角形的三个顶点都在正方形网格线的交点上时,我们称三角形为格点三角形.
 (1)、如图1,请在图1中标出的外接圆的圆心O的位置;(2)、请在图2中画一个格点三角形与原三角形相似。18. 如图,已知为的直径,是弦,于E , 于F , 连接 , , .
(1)、如图1,请在图1中标出的外接圆的圆心O的位置;(2)、请在图2中画一个格点三角形与原三角形相似。18. 如图,已知为的直径,是弦,于E , 于F , 连接 , , . (1)、求证:;(2)、若 , 求的值及阴影部分的面积.19. 已知某二次函数图象上两点坐标分别为; , 与x轴的一个交点为 , D为顶点坐标.(1)、求出该二次函数表达式(2)、求出的面积20. 如图,已知中, , 以为直径的交于点D , 交于点E , 连结 , 相交于点F.
(1)、求证:;(2)、若 , 求的值及阴影部分的面积.19. 已知某二次函数图象上两点坐标分别为; , 与x轴的一个交点为 , D为顶点坐标.(1)、求出该二次函数表达式(2)、求出的面积20. 如图,已知中, , 以为直径的交于点D , 交于点E , 连结 , 相交于点F. (1)、求证:(2)、若 , , 求的长。21. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件,设每天的销售利润为W元.(1)、当销售价为每件30元时,每天的销售量为多少件;(2)、若商场要每天获得销售利润2000元,销售单价应定为多少元?(3)、求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?22.
(1)、求证:(2)、若 , , 求的长。21. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件,设每天的销售利润为W元.(1)、当销售价为每件30元时,每天的销售量为多少件;(2)、若商场要每天获得销售利润2000元,销售单价应定为多少元?(3)、求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?22. (1)、【基础巩固】
(1)、【基础巩固】如图1,在中,D , E分别在 , 上,连结DE,若 , 求证:.
(2)、【尝试应用】如图2,在中,在上取一点E , 以为一边构造平行四边形 , 使点D , F恰好落在 , 上,连结 , 若 , , , 求的长.
(3)、【拓展提高】如图3,在中,在上取一点E , 以为一边构造平行四边形 , 使点F恰好落在上,连结 , , 若 , , , , 求的长。
23. 如图1,为四边形的外接圆,与相交于点 , 且 , 连结 , 设. (1)、用含的代数式表示.(2)、如图2,连结 , 交于点 , 若 , 求证:.(3)、在(2)的基础上,当 , 时,求出的值.
(1)、用含的代数式表示.(2)、如图2,连结 , 交于点 , 若 , 求证:.(3)、在(2)的基础上,当 , 时,求出的值.