浙江省台州市和合教育联盟2023-2024学年八年级第一学期数学期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列运动图标中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点关于y轴对称的点B的坐标为( )A、(2,3) B、(2,3) C、(2,3) D、(3,2)3. 两根木棒的长度分别为5cm,8cm,取第三根木棒,使它们首尾顺次相接组成一个三角形,则第三根木棒的长度可以是( )A、2cm B、3cm C、6cm D、15cm4. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 下列命题属于假命题的是( )A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等6. 如图,在△ABC中,作BC边上的高线,下列画法正确的是( )A、
2. 点关于y轴对称的点B的坐标为( )A、(2,3) B、(2,3) C、(2,3) D、(3,2)3. 两根木棒的长度分别为5cm,8cm,取第三根木棒,使它们首尾顺次相接组成一个三角形,则第三根木棒的长度可以是( )A、2cm B、3cm C、6cm D、15cm4. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 下列命题属于假命题的是( )A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等6. 如图,在△ABC中,作BC边上的高线,下列画法正确的是( )A、 B、
B、 C、
C、 D、
D、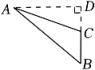 7. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
7. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( ) A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC8. 一个等腰三角形的一个外角为130 , 那么这个三角形的底角度数为( )A、65 B、50 C、50或40 D、65或509. 如图,在中,过点B作的角平分线的垂线,垂足为F,交于点G,若 , 则线段的长为( )
A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC8. 一个等腰三角形的一个外角为130 , 那么这个三角形的底角度数为( )A、65 B、50 C、50或40 D、65或509. 如图,在中,过点B作的角平分线的垂线,垂足为F,交于点G,若 , 则线段的长为( ) A、1 B、2 C、2.5 D、310. 如下图所示,∠BAD=∠CAE=90°,AB=AD,AE=AC,D在CE上,F是CB延长线上一点,AF⊥BC,下列结论:①∠ACF=45°;②四边形ABCD的面积等于AC2;③CE=2AF;④S△BCD=S△ABF+S△ADE其中正确的是( )
A、1 B、2 C、2.5 D、310. 如下图所示,∠BAD=∠CAE=90°,AB=AD,AE=AC,D在CE上,F是CB延长线上一点,AF⊥BC,下列结论:①∠ACF=45°;②四边形ABCD的面积等于AC2;③CE=2AF;④S△BCD=S△ABF+S△ADE其中正确的是( ) A、①② B、②③ C、①②③ D、①②③④
A、①② B、②③ C、①②③ D、①②③④二、填空题(本题有6小题,每小题4分,共24分)
-
11. 一个正五边形的内角和为 .12. 点P(m , 2)关于x轴的对称点P'的坐标是(1,3-n),则m+n的值为 .13. 若等腰三角形的两边长分别为3cm , 8cm , 则它的周长是 .14. 如图,在中, , , , 将沿折叠,点B的对应点是点 , 则的度数是 .
 15. 当三角形中一个内角是另一个内角的两倍时,称此三角形为“特征三角形”,如果一个“特征三角形”是等腰三角形,那么这个“特征三角形”的最小内角的度数为.16. 如图,中, , , , 平分 , 如果点P,点G分别为 , 上的动点,那么的最小值是.
15. 当三角形中一个内角是另一个内角的两倍时,称此三角形为“特征三角形”,如果一个“特征三角形”是等腰三角形,那么这个“特征三角形”的最小内角的度数为.16. 如图,中, , , , 平分 , 如果点P,点G分别为 , 上的动点,那么的最小值是.
三、解答题(本题有8小题,其中17、18、19每题6分,20、21每题8分,22,23每题10分,24题12分)
-
17. 一个多边形内角和为1080 , 求这个多边形的边数。18. 在由边长为1个单位长度的小正方形组成的网格中建立直角坐标系,△ABC的位置如图所示.
 (1)、试在网格图中画出△A1B1C1 , 使△A1B1C1与△ABC关于x轴对称.(2)、在x轴上找一点P,使得PA+PB最小19. 如图,已知 , 分别是边上的高和中线,若 , , , .
(1)、试在网格图中画出△A1B1C1 , 使△A1B1C1与△ABC关于x轴对称.(2)、在x轴上找一点P,使得PA+PB最小19. 如图,已知 , 分别是边上的高和中线,若 , , , . (1)、求的长度.(2)、求的面积.20. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
(1)、求的长度.(2)、求的面积.20. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.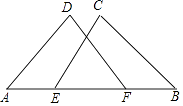 21. 如图,为的角平分线,于点 , 于点 , 交于点
21. 如图,为的角平分线,于点 , 于点 , 交于点
求证:垂直平分 .
22. 如图,点 , 分别是正五边形的边 , 上的点,且 , 交点 . (1)、求证:≌ .(2)、求的度数.23. 如图,在△ABC中,∠ABC=2∠ACB,BD为△ABC的角平分线;
(1)、求证:≌ .(2)、求的度数.23. 如图,在△ABC中,∠ABC=2∠ACB,BD为△ABC的角平分线; (1)、若AB=BD,则∠A的度数为 °(直接写出结果);(2)、如图1,若E为线段BC上一点,∠DEC=∠A;求证:AB=EC.(3)、如图2,若E为线段BD上一点,∠DEC=∠A,求证:AB=EC.24. 如图,已知△ABC是边长为8cm(可求得高为4√3cm)的等边三角形,边AB在射线OM上,且OA=12cm,点D从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,以CD为边作等边三角形CDE,连结BE.
(1)、若AB=BD,则∠A的度数为 °(直接写出结果);(2)、如图1,若E为线段BC上一点,∠DEC=∠A;求证:AB=EC.(3)、如图2,若E为线段BD上一点,∠DEC=∠A,求证:AB=EC.24. 如图,已知△ABC是边长为8cm(可求得高为4√3cm)的等边三角形,边AB在射线OM上,且OA=12cm,点D从O点出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,以CD为边作等边三角形CDE,连结BE.
 (1)、证明:△CAD≌△CBE;(2)、如图2,当12<t<20时,求△BDE的周长的最小值;(3)、当点D在射线OM上运动(即t≥0)时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由。
(1)、证明:△CAD≌△CBE;(2)、如图2,当12<t<20时,求△BDE的周长的最小值;(3)、当点D在射线OM上运动(即t≥0)时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由。