浙江省杭州市十三中教育集团期中考试2023-2024学年九年级上学期数学11月期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 已知 , 则下列各式正确的是( )A、 B、 C、 D、2. 下列事件中,属于必然事件的是( )A、在一个装着白球和黑球的袋中摸出红球 B、三角形三个内角的和小于180° C、在一张纸上任意画两条线段,这两条线段相交 D、若a是实数,则a2≥03. 将二次函数y=3x2的图象先向左平移2个单位,再向上平移4个单位后,得到的抛物线的表达式为( )A、y=3(x-2)2+4 B、y=3(x+2)2+4 C、y=3(x+2)2-4 D、y=3(x-2)2-44. 如图,直线l1∥l2∥l3 , 若AB=2,BC=4,DE=3,则DF=( )
 A、5 B、6 C、8 D、95. 下列命题正确的是( )A、三个点确定一个圆 B、圆是轴对称图形,其对称轴是直径 C、90°的圆周角所对的弦是直径 D、平分弦的直径垂直于弦6. 如图,正五边形ABCDE内接于⊙O , 连结OC , OD , 则∠COD=( )
A、5 B、6 C、8 D、95. 下列命题正确的是( )A、三个点确定一个圆 B、圆是轴对称图形,其对称轴是直径 C、90°的圆周角所对的弦是直径 D、平分弦的直径垂直于弦6. 如图,正五边形ABCDE内接于⊙O , 连结OC , OD , 则∠COD=( )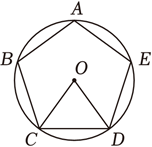 A、72° B、60 C、54 D、48°7. 已知m=6,关于x的一元二次方程(x+3)(x-4)-m=0的解为x1 , x2(x1<x2),则下列结论正确的是( )A、x1<-3<4<x2 B、-3<x1<4<x2 C、-3<x1<x2<4 D、x1<-3<x2<48. 为迎接校庆,我校音乐社团购买了一种乐器,如图,乐器上的一根弦AB=60cm , 两个端点A , B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C , D之间的距离为( )
A、72° B、60 C、54 D、48°7. 已知m=6,关于x的一元二次方程(x+3)(x-4)-m=0的解为x1 , x2(x1<x2),则下列结论正确的是( )A、x1<-3<4<x2 B、-3<x1<4<x2 C、-3<x1<x2<4 D、x1<-3<x2<48. 为迎接校庆,我校音乐社团购买了一种乐器,如图,乐器上的一根弦AB=60cm , 两个端点A , B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C , D之间的距离为( ) A、()cm B、()cm C、()cm D、()cm9. 如图,抛物线y1=a(x+2)2-3与y2=(x-3)2+1相交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B , C.有下列结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=5;④2AB=3AC , 其中正确的有( )
A、()cm B、()cm C、()cm D、()cm9. 如图,抛物线y1=a(x+2)2-3与y2=(x-3)2+1相交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B , C.有下列结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=5;④2AB=3AC , 其中正确的有( )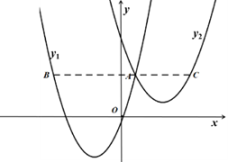 A、①② B、①③ C、③④ D、①④10. 已知等腰直角三角形OAC , ∠OAC=90°,以O为圆心,OA为半径的圆交OC于点F , 过点F作AC的垂线交⊙O于点E , 交AC于点B.连结AE , 交OC于点D , 若OD= , 则AB的长为( )
A、①② B、①③ C、③④ D、①④10. 已知等腰直角三角形OAC , ∠OAC=90°,以O为圆心,OA为半径的圆交OC于点F , 过点F作AC的垂线交⊙O于点E , 交AC于点B.连结AE , 交OC于点D , 若OD= , 则AB的长为( )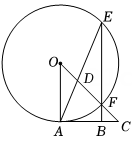 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题4分,共24分)
-
11. 已知⊙O的面积为25π,点P在圆上,则OP= .12. 在三张完全相同的卡片上,分别画有正三角形、正方形、正五边形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率是 .13. 已知二次函数y=x2-4x+5,则其顶点关于y轴对称的点的坐标为 .14. 已知△ABC的边BC= , 且△ABC内接于半径为4cm的⊙O , 则∠A的度数为 .15. 对于一个函数,自变量x取a时,函数值y也等于a , 则称a是这个函数的幸运数.已知二次函数y=x2+4x+m .(1)、若5是此函数的幸运数,则m的值为 .(2)、若此函数有两个相异的幸运数a , b , 且a<2<b , 则m的取值范围为 .16. 如图,△ABC是⊙O的内接等腰三角形,∠ABC=30°,弦EF过AB边的中点D , 且EF∥BC , 若BC= , 则外接圆的半径为 , EF=.

三、解答题(共66分)
-
17. 如图,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6)在给出的平面直角坐标系中:
 (1)、画出△ABC绕点A顺时针旋转90°后得到的△AB1C1;并直接写出B1 , C1的坐标;(2)、计算点B旋转到点B1位置时,经过的路径弧BB1的长度.18. 在一个不透明的盒子里装有除颜色外其余均相同的1个黄色球和若干个白色球,从盒子里随机摸出一个乒乓球,摸到黄球的概率是.(1)、白球的个数为个.(2)、现从盒子中摸球,摸出一个球,记下颜色后放回,再从中随机摸出一个球.请通过列表或画树状图的方法,求两次摸到相同颜色球的概率.19. 如图,△ABC∽△ACD .
(1)、画出△ABC绕点A顺时针旋转90°后得到的△AB1C1;并直接写出B1 , C1的坐标;(2)、计算点B旋转到点B1位置时,经过的路径弧BB1的长度.18. 在一个不透明的盒子里装有除颜色外其余均相同的1个黄色球和若干个白色球,从盒子里随机摸出一个乒乓球,摸到黄球的概率是.(1)、白球的个数为个.(2)、现从盒子中摸球,摸出一个球,记下颜色后放回,再从中随机摸出一个球.请通过列表或画树状图的方法,求两次摸到相同颜色球的概率.19. 如图,△ABC∽△ACD . (1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.20. 如图,⊙O的直径BC为6cm , 弦AC为3cm . ∠CAB的平分线交⊙O于点D.
(1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.20. 如图,⊙O的直径BC为6cm , 弦AC为3cm . ∠CAB的平分线交⊙O于点D. (1)、求∠CBD的度数.(2)、求阴影部分的面积.21. 如图,小明、小红两人分别跑步从相距5km的A , C两地同时出发,各自沿箭头所指方向前进.已知小明的速度是8km/h , 小红的速度是6km/h , 且当小明到达C地时两人停止运动,且AC⊥CD.设小明运动的时间为t(h),小明与小红的距离为s(km).
(1)、求∠CBD的度数.(2)、求阴影部分的面积.21. 如图,小明、小红两人分别跑步从相距5km的A , C两地同时出发,各自沿箭头所指方向前进.已知小明的速度是8km/h , 小红的速度是6km/h , 且当小明到达C地时两人停止运动,且AC⊥CD.设小明运动的时间为t(h),小明与小红的距离为s(km). (1)、写出s与t的关系式.(2)、当小明与小红出发多少时间后,两人相距离千米?(3)、出发多少时间后两人相距最近?最近距离为多少千米?22. 如图,某公路上有一隧道,顶部是圆弧形拱顶,圆心为O , 隧道的水平宽AB为24m , AB离地面的高度AE=10m , 拱顶最高处C离地面的高度CD为18m.若在拱顶的M , N处安装照明灯,且M , N离地面的高度相等,都为17m.
(1)、写出s与t的关系式.(2)、当小明与小红出发多少时间后,两人相距离千米?(3)、出发多少时间后两人相距最近?最近距离为多少千米?22. 如图,某公路上有一隧道,顶部是圆弧形拱顶,圆心为O , 隧道的水平宽AB为24m , AB离地面的高度AE=10m , 拱顶最高处C离地面的高度CD为18m.若在拱顶的M , N处安装照明灯,且M , N离地面的高度相等,都为17m.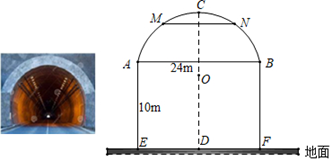 (1)、求圆弧形拱顶的半径的长度.(2)、求MN的长度.
(1)、求圆弧形拱顶的半径的长度.(2)、求MN的长度.