浙江省杭州市十三中教育集团期中考试2023-2024学年七年级上学期数学11月期中试卷

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分。每小题只有一个选项符合题意）

1. 下列各组数中，互为相反数的是（）

A、6和 $- 6$ B、 $- 6$ 和 $\frac{1}{6}$ C、 $- 6$ 和 $- \frac{1}{6}$ D、 $\frac{1}{6}$ 和6

查看试题解析
2. 杭州市2022年 $G D P$ 超过了18000亿元，18000亿用科学记数法表示为（）

A、1.8 $\times$ 10⁴ B、18 $\times$ 10¹¹ C、1.8 $\times$ 10¹² D、1.8 $\times$ 10¹¹

查看试题解析
3. 下列说法错误的是（）

A、 $m$ 、 $n$ 互为倒数，则 $m n = 1$ B、绝对值等于本身的是非负数 C、 $-$ 2⁵表示5个 $- 2$ 相乘 D、若一个数减去一个正数，差一定小于被减数

查看试题解析
4. 下列各数314， $\frac{π}{3}$ ， $0 . \dot{4}$ ， $\sqrt{16}$ ， $2.1313313331 \dots$ （相邻两个1之间3的个数逐次多1）， $\frac{23}{21}$ ， $\sqrt{7}$ ，其中有理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 一件校服，按标价的6折出售，售价是 $x$ 元，这件校服的标价是（）

A、 $0.6 x$ 元 B、 $\frac{x}{0.4}$ 元 C、 $0.4 x$ 元 D、 $\frac{x}{0.6}$ 元

查看试题解析
6. 正方形面积为10，其边长是x，以下说法正确的是（）

A、x是有理数 B、2＜x＜3 C、3＜x＜4 D、在数轴上找不到表示实数x的点

查看试题解析
7. 下列说法正确的是（）

A、 $\sqrt{64}$ 的立方根是2 B、 $- 3$ 是27负的立方根 C、 $\frac{125}{216}$ 的立方根是 $\pm \frac{5}{6}$ D、 $(- 1)^{2}$ 的立方根是 $- 1$

查看试题解析
8. 下列说法中，正确的个数有（）
①数轴上的点都表示有理数； ②若 $a < 0$ ， $b < 0$ ，则 $a + b = - (| a | + | b |)$ ；
③几个有理数相乘，积的符号由负因数的个数决定；
④小于2014且大于 $- 2013$ 的所有整数的和是2013；
⑤在1和3之间的无理数有且只有 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ ， $\sqrt{7}$ 这4个．

A、2 B、3 C、4 D、5

查看试题解析
9. 已知数 $a$ 、 $b$ 在数轴上的位置如图所示，下列结论：①ab＜0；②a+b＞0；③a³＞b³；④（a﹣b）³＞0；⑤a＜ $-$ b＜b＜ $-$ a；⑥ $| b - a | - | a | = b$ ．其中正确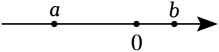的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，1925年数学家莫伦发现了世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形．如果标注A ， B的正方形边长分别为x ， y ，则标注E的正方形的边长（）

A、2y﹣3x B、3y﹣3x C、3y﹣2x D、2y﹣2x

查看试题解析

二、填空题（每小题4分，共24分）

11. 小华今年a岁，小明比他小2岁，则小明的年龄是岁．

查看试题解析
12. 3.14精确到0.1是， 3.98万是精确到位．

查看试题解析
13. 若a、b互为相反数，c是最大的负整数，则代数式 $\frac{a}{b} - c^{2}$ = ．

查看试题解析
14. 若 $2 + \sqrt{7}$ 的整数部分为a ，小数部分为b ，则a= ， a $-$ b= ．

查看试题解析
15. 有理数a、b、c在数轴上的位置如图所示，化简： $|a - b| + |b - c| - |c - a| =$ ．

查看试题解析
16. 一列数a₁ ， a₂ ， a₃ ， ……，a_n ，其中 $a_{1} = - 3$ ， $a_{2} = \frac{1}{1 - a_{1}}$ ， $a_{3} = \frac{1}{1 - a_{2}}$ ， ……， $a_{n} = \frac{1}{1 - a_{n - 1}}$ ，则 $a_{1} \times a_{2} \times a_{3} \times \dots \dots \times a_{2023} =$ ； $a_{1} + a_{2} + a_{3} + \dots \dots + a_{37} =$ ．

查看试题解析

三、解答题（共66分，解答应写出必要的文字说明、证明过程或演算步骡）

17. 在数轴上表示下列各数，并把它们按照从小到大的顺序排列．
$- (- 2)$ ， $- 2^{2}$ ， 0， $- | - 3 |$ ， π ， $- 4 \frac{1}{2}$ ．

查看试题解析
18. 计算：

(1)、2 $-$ 23+35；

(2)、 ${- 1}^{2} \times {(- 2)}^{3} + \sqrt{{(- 3)}^{2}} - \sqrt[3]{- 64}$

查看试题解析
19. 如图，根据图中所给条件解答下列各题：

(1)、用含x ， y的式子表示图中阴影部分的周长；

(2)、当x＝1.5，y＝0.5时，求图中阴影部分的周长．

查看试题解析
20.

(1)、若a、b互为相反数，c、d互为倒数，并且m的立方等于它的本身．求 $\frac{2 a + 2 b}{m + 2} + c d$ 的值.

(2)、已知当x= $-$ 1时，ax³ $-$ bx+c=5，则当x= $-$ 1时，求代数式7 $+$ ax⁴ $-$ bx² $-$ c的值.

查看试题解析
21. 在杭州亚运会期间，出租车司机小张某天以家为出发地在东西方向营运.如果规定向东为“正”，向西为“负”，他这天上午的行程可以表示为：+3，+6，-5，+4，-3，+2，-7，+3，-9，+5（单位：千米）.借助数轴，解决以下问题：

(1)、小张将最后一名乘客送达目的地后需要返回出发地，请问小张该如何行驶才能回到出发地？

(2)、该马路东西方向上至少有多少千米？

(3)、若汽车耗油量为0.6升/千米，发车前油箱有28.5升汽油，若小张将最后一名乘客送达目的地，再返回出发地，问小张今天上午是否需要加油？若要加油至少需要加多少才能返回出发地？若不用加油，请说明理由.

查看试题解析
22. 在学习一个数的绝对值过程中，化简|a|时，可以这样分类：当a＞0时，|a|＝a；当a＝0时，|a|＝0；当a＜0时，|a|＝ $-$ a ．请用这种方法解决下列问题．

(1)、当a＝3时，则 $\frac{a}{|a|}$ ＝；当a＝ $-$ 2时，则 $\frac{a}{|a|}$ ＝．

(2)、已知a ， b是有理数，当ab＞0时，试求 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值．

(3)、已知a ， b ， c是非零有理数，满足a+b+c＝0且 $\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} ＝$ 1，求 $\frac{b + c}{|a|} + \frac{a + c}{|b|} + \frac{a + b}{|c|}$ 的值．

查看试题解析
23. 数轴是初中数学中一个重要的工具，研究数轴可以发现许多重要的规律．如数轴上的点A、点B表示的数分别为a、b ，则A、B两点之间的距离AB＝|a $-$ b|，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．
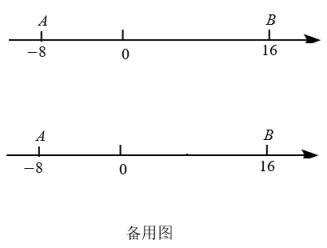
解决问题：现数轴上有一点A表示的数为﹣8，点B表示的数为16，点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度向左匀速运动，设运动的时间为t秒（t＞0）．

(1)、则A、B两点之间的距离AB＝，到A、B两点距离相等的点表示的数是．

(2)、求当t为何值时，PQ＝ $\frac{1}{4}$ AB ．

(3)、折叠数轴使点P与Q重合，折点记为M ，还原后再折叠数轴使点B与Q重合，折点记为N ，点P和点Q在运动过程中，线段MN的中点E的位置是否发生变化？若不变，请求出线段MN的中点E表示的数；若改变，请说明理由.

查看试题解析