沪科版数学九年级上册第23.1锐角的三角函数(专题汇编)
试卷更新日期:2023-11-24 类型:同步测试
一、锐角三角函数值计算
-
1.(1)、(2)、(3)、(4)、2. 计算:3. 计算(1)、;(2)、 .4. 计算.
二、与解直角三角形相关作图题
-
5. 如图,AD是△ABC的中线,tanB= ,cosC= ,AC=
 (1)、求BC的长;(2)、作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.6. 如图,在 的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段 的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
(1)、求BC的长;(2)、作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.6. 如图,在 的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段 的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹. (1)、在图①中画一条射线 ,使 .(2)、在图②中画一条射线 ,使 .7. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
(1)、在图①中画一条射线 ,使 .(2)、在图②中画一条射线 ,使 .7. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形. (1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .
(1)、在图①中找到一个格点C , 使∠ABC是锐角,且tan∠ABC= ,并画出△ABC .(2)、在图②中找到一个格点D , 使∠ADB是锐角,且tan∠ADB=1,并画出△ABD .三、与反比例函数、相似结合
-
8. 如图,点B是双曲线y= (k≠0)上的一点,点A在x轴上,且AB=2,OB⊥AB , 若∠BAO=60°,求k的值.
 9. 如图,一次函数的图象与y轴交于点A , 与反比例函数的图象交于点和点 , 连接 .
9. 如图,一次函数的图象与y轴交于点A , 与反比例函数的图象交于点和点 , 连接 .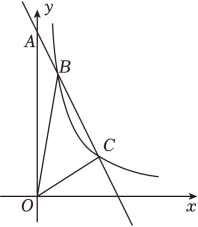 (1)、求的值;(2)、求的面积.10. 如图,在平面直角坐标系中,点P在反比例函数的图象上,点A , B在x轴上,且 , 垂足为P , PA交y轴于点C , , 的面积是2.则k的值是( )
(1)、求的值;(2)、求的面积.10. 如图,在平面直角坐标系中,点P在反比例函数的图象上,点A , B在x轴上,且 , 垂足为P , PA交y轴于点C , , 的面积是2.则k的值是( )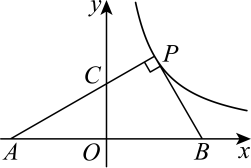 A、1 B、 C、 D、211. 如图,点A在双曲线上,连接 , 作 , 交双曲线于点B , 连接 . 若 , 则k的值为( )
A、1 B、 C、 D、211. 如图,点A在双曲线上,连接 , 作 , 交双曲线于点B , 连接 . 若 , 则k的值为( ) A、1 B、2 C、 D、1612. 如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数 , 在第一象限内的图像交于点B,连接 , 若 , , 则m的值是( )
A、1 B、2 C、 D、1612. 如图,在平面直角坐标系中,直线与y轴交于点C,与反比例函数 , 在第一象限内的图像交于点B,连接 , 若 , , 则m的值是( )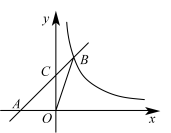 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12四、与二次函数,相似结合
-
13. 如图,在平面直角坐标系中,抛物线经过点 , 顶点为A,连结 .
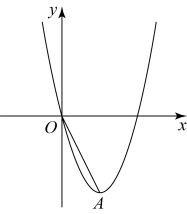 (1)、求a的值.(2)、求A的坐标.(3)、P为x轴上的动点,当时,请直接写出OP的长.14. 如图,直线与轴交于点 , 与轴交于 , 抛物线经过、两点,与轴正半轴交于点 , 为抛物线的顶点,连接 .
(1)、求a的值.(2)、求A的坐标.(3)、P为x轴上的动点,当时,请直接写出OP的长.14. 如图,直线与轴交于点 , 与轴交于 , 抛物线经过、两点,与轴正半轴交于点 , 为抛物线的顶点,连接 .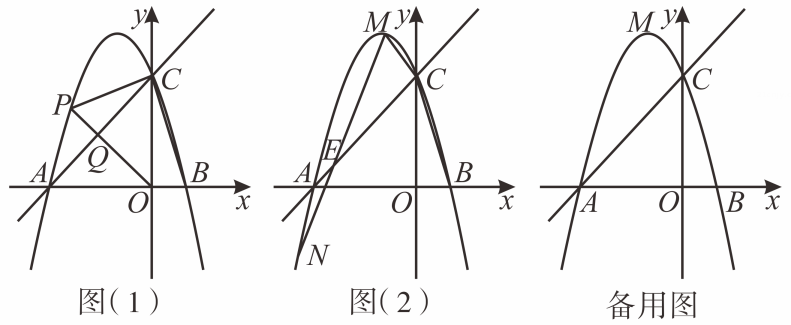 (1)、求抛物线的解析式及顶点的坐标;(2)、如图 , 点为直线上方的抛物线上的一点,连接、、 , 交于点 , 若将的面积分为:两部分,求点的坐标;(3)、如图 , 若点是第三象限的抛物线上一点,连接 , 交直线于 , 当时,求点的坐标;(4)、在(3)的条件下,若是轴上的一个动点,请直接写出的最小值.
(1)、求抛物线的解析式及顶点的坐标;(2)、如图 , 点为直线上方的抛物线上的一点,连接、、 , 交于点 , 若将的面积分为:两部分,求点的坐标;(3)、如图 , 若点是第三象限的抛物线上一点,连接 , 交直线于 , 当时,求点的坐标;(4)、在(3)的条件下,若是轴上的一个动点,请直接写出的最小值.五、胡不归最值相关
-
15. 如图,在中, , , 交于点D , P为线段上的动点,则的最小值为 .
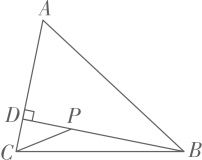 16. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .
16. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .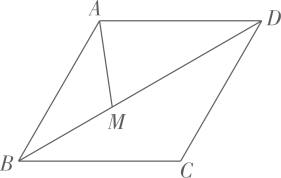
六、与勾股定理相关
-
17. 如图,在中, , 点为的中点,于点 , 连接 , 已知 .
 (1)、若 , 求的长度;(2)、若 , 求 .18. 如图,中, , D是的中点,交AC于点E, . 求的正切值.
(1)、若 , 求的长度;(2)、若 , 求 .18. 如图,中, , D是的中点,交AC于点E, . 求的正切值. 19. 如图,在中, , 延长斜边BC到点D,使 , 联结AD,如果 , 求的值.
19. 如图,在中, , 延长斜边BC到点D,使 , 联结AD,如果 , 求的值. 20. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
20. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.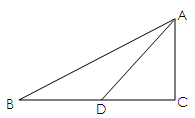 21. 如图,在边长相同的小正方形网格中,点、、、都在这些小正方形的顶点上,与相交于点 , 则的值为 .
21. 如图,在边长相同的小正方形网格中,点、、、都在这些小正方形的顶点上,与相交于点 , 则的值为 . 22. 如图,在正方形网格中每个小正方形的边长都是 , 小正方形的顶点称为格点,的顶点都在格点上,则的正切值是( )
22. 如图,在正方形网格中每个小正方形的边长都是 , 小正方形的顶点称为格点,的顶点都在格点上,则的正切值是( ) A、
A、
B、
C、
D、23. 如图,在中, , 于 , 平分交于 , , 则的值为( )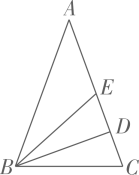 A、 B、 C、 D、24. 如图,点是矩形纸片边上一点,如果沿着折叠矩形纸片,恰好使点落在边上的点处,已知 , , 那么折痕的长是 .
A、 B、 C、 D、24. 如图,点是矩形纸片边上一点,如果沿着折叠矩形纸片,恰好使点落在边上的点处,已知 , , 那么折痕的长是 .
七、综合题