浙江省台州市温岭市团队六校2023-2024学年九年级上学期数学期中试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题:本大题有10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 抛物线y=2(x﹣3)2的顶点坐标为( )A、(3,0) B、(﹣3,0) C、(0,3) D、(0,﹣3)2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
3. 解一元二次方程x2+4x﹣1=0,配方正确的是( )A、(x+2)2=3 B、(x﹣2)2=3 C、(x+2)2=5 D、(x﹣2)2=54. 抛物线y=x2先向下平移1个单位,再向右平移2个单位,所得函数的解析式为( )A、y=x2﹣2x﹣1 B、y=x2﹣4x+3 C、y=x2+4x﹣3 D、y=x2﹣2x+15. 如图,点A , B , C , D四点均在⊙O上,∠AOD=68°,AO∥DC , 则∠B的度数为( )
斐波那契螺旋线
3. 解一元二次方程x2+4x﹣1=0,配方正确的是( )A、(x+2)2=3 B、(x﹣2)2=3 C、(x+2)2=5 D、(x﹣2)2=54. 抛物线y=x2先向下平移1个单位,再向右平移2个单位,所得函数的解析式为( )A、y=x2﹣2x﹣1 B、y=x2﹣4x+3 C、y=x2+4x﹣3 D、y=x2﹣2x+15. 如图,点A , B , C , D四点均在⊙O上,∠AOD=68°,AO∥DC , 则∠B的度数为( ) A、40° B、60° C、56° D、68°6. 电影《八角笼中》讲述了向腾辉倾注心血想把当地无人照料的孩子培养成才,这让生活本没有出路的孩子们看到了一丝通向未来的曙光的故事。一经上映就获得追捧,第一天票房收入约6亿元,第三天票房收入达到了8.64亿元,设第一天到第三天票房收入平均每天增长的百分率为x , 则可列方程( )A、6(1+x)=8.64 B、6(1+2x)=8.64 C、6(1+x)2=8.64 D、6(1﹣x)2=8.647. 函数y=ax2与y=﹣ax+b的图象可能是( )A、
A、40° B、60° C、56° D、68°6. 电影《八角笼中》讲述了向腾辉倾注心血想把当地无人照料的孩子培养成才,这让生活本没有出路的孩子们看到了一丝通向未来的曙光的故事。一经上映就获得追捧,第一天票房收入约6亿元,第三天票房收入达到了8.64亿元,设第一天到第三天票房收入平均每天增长的百分率为x , 则可列方程( )A、6(1+x)=8.64 B、6(1+2x)=8.64 C、6(1+x)2=8.64 D、6(1﹣x)2=8.647. 函数y=ax2与y=﹣ax+b的图象可能是( )A、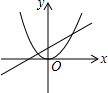 B、
B、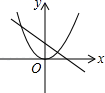 C、
C、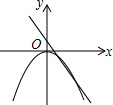 D、
D、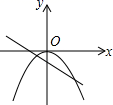 8. 我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+2x-35=0即x(x+2)=35为例说明,记载的方法是:构造如图,大正方形的面积是(x+x+2)2 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即4×35+22 , 因此x=5.则在下面四个构图中,能正确说明方程x2-5x-6=0解法的构图是( )
8. 我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程x2+2x-35=0即x(x+2)=35为例说明,记载的方法是:构造如图,大正方形的面积是(x+x+2)2 . 同时它又等于四个矩形的面积加上中间小正方形的面积,即4×35+22 , 因此x=5.则在下面四个构图中,能正确说明方程x2-5x-6=0解法的构图是( )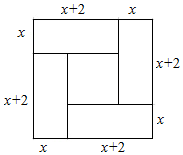 A、
A、 B、
B、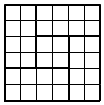 C、
C、 D、
D、 9. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A , B , C . 如下四个推断:
9. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A , B , C . 如下四个推断:
①抛物线开口向下;
②当x=﹣2时.y取最大值;
③当m≤4时,关于x的一元二次方程ax2+bx+c=m总有两个不相等的实数根;
④若直线y=kx+c(k≠0)经过点A , C , 当kx+c>ax2+bx+c时,x的取值范围是﹣4<x<0.
其中推断正确的有( ).
A、1个 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=4 , ∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )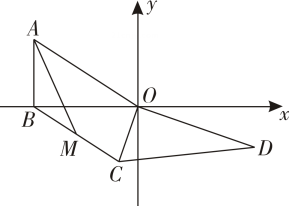 A、3 B、6-4 C、2-2 D、2
A、3 B、6-4 C、2-2 D、2二、填空题:本大题有6个小题,每小题4分,共24分.
-
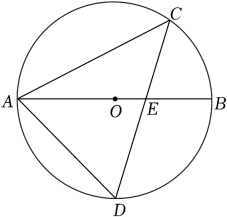
11. 请写出一个开口向上,并且与y轴交于点(0,2)的抛物线的表达式: .12. 请写出一个常数c的值,使得关于x的方程x22x+c=0有两个不相等的实数根,则c的值可以是 .13. 已知点P(﹣b , 2)与点Q(3,2a)关于原点对称,则ab的值是 .14. 如图,AB是⊙O的直径,弦CD交AB于点E , 连接AC , AD . 若∠D=62°,则∠BAC= .
 15. 如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形ABC , 点A在圆内,且AC恰好经过点O , 其中BC=12,OA=8,则BD的长为 .
15. 如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形ABC , 点A在圆内,且AC恰好经过点O , 其中BC=12,OA=8,则BD的长为 .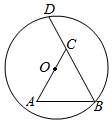 16. 如图,已知抛物线y1的开口向上且顶点D在y轴的负半轴上,y2由y1先绕顶点旋转180°,再平移得到,它们与x轴的交点为A、B、C且AB=BC=2OD=4,则抛物线y2的顶点E的坐标是;若过定点(1,1)的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为.
16. 如图,已知抛物线y1的开口向上且顶点D在y轴的负半轴上,y2由y1先绕顶点旋转180°,再平移得到,它们与x轴的交点为A、B、C且AB=BC=2OD=4,则抛物线y2的顶点E的坐标是;若过定点(1,1)的直线被抛物线y1、y2所截得的线段长相等,则这条直线的解析式为.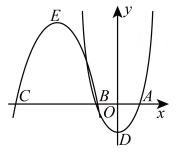
三、解答题:本大题有7个小题,共66分.
-
17. 解方程:(1)、x2﹣2x﹣8=0.(2)、(x﹣2)2=2x﹣4.18. 如图,在⊙O中,0A , OB为⊙O的半径,点C为优弧AB的中点,AD=BE.
求证:CD=CE.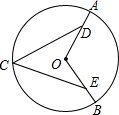 19. 已知二次函数y=﹣x2﹣2x+3.
19. 已知二次函数y=﹣x2﹣2x+3. (1)、将二次函数化成y=a(x﹣h)2+k的形式;(2)、在平面直角坐标系中画出y=﹣x2﹣2x+3的图象;(3)、结合函数图象,直接写出y>0时x的取值范围.20. 已知:如图在△ABC中,AB=AC , ∠BAC=150°,线段AC绕点C逆时针旋转90°得到线段CD , 连接AD , BD , 过点B作BE⊥CD于点E.
(1)、将二次函数化成y=a(x﹣h)2+k的形式;(2)、在平面直角坐标系中画出y=﹣x2﹣2x+3的图象;(3)、结合函数图象,直接写出y>0时x的取值范围.20. 已知:如图在△ABC中,AB=AC , ∠BAC=150°,线段AC绕点C逆时针旋转90°得到线段CD , 连接AD , BD , 过点B作BE⊥CD于点E.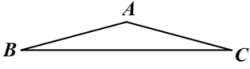 (1)、依题意补全图形;
(1)、依题意补全图形;
(2)、求∠DBE的度数.
(3)、若AB=4,求△ABD的面积.
21. 已知⊙O的弦AB的长等于⊙O的半径,求此弦AB所对的圆周角的度数.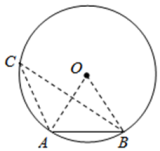
安安的解题过程如下:
【解】如图所示,连接OA , OB , 在优弧AB上任取一点C , 连接CA , CB . 因为AB=OA=OB , 所以∠AOB=60°,所以∠ACB=∠AOB=30°,即弦AB所对的圆周角等于30°.
(1)、请问安安的解题过程正确吗?如果不正确,请写出正确的解题步骤.(2)、归纳:在同园中,同弦或等弦所对的圆周角的关系是.22. 如图,点P是正方形ABCD内的一点,连接CP , 将线段CP绕点C顺时针旋转90°,得到线段CQ , 连接BP , DQ .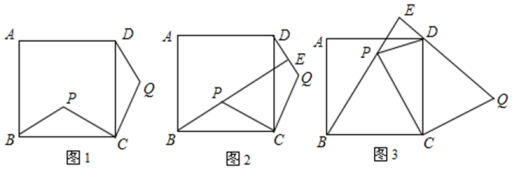 (1)、如图1,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E .
(1)、如图1,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E .①如图2,求证:BE⊥DQ;
②如图3,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
23. 定义:若一个函数图象上存在纵坐标与横坐标互为相反数的点,则称该点为这个函数图象的“互逆点”
(1)、若点M(-2,m)是一次函数y=kx+6的图象上的“互逆点”,则k=若点N(n , -n)是函数y的图象上的“互逆点”,则n=
(2)、若点P(p , 3)是二次函数y=x2+bx+c的图象上唯一的“互逆点”,求这个二次函数的表达式;
(3)、若二次函数y=ax2+bx+c(a , b是常数,a>0)的图象过点(0,2),且图象上存在两个不同的“互逆点”A(x1 , -x1),B(x2 , -x2),且满足-1<x1<1,|x1x2|=2,如果z=b2+2b+2,请求出z的取值范围。