浙江省绍兴市新昌县部分校2023-2024学年九年级上学期数学期中联考试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(每小题有4个选项,其中有且只有一个正确,请把正确选项的编码填入答题卷的相应空格,每小题3分,共30分)
-
1. 下列事件是必然事件的是( )A、在学校操场上抛出的篮球会落下 B、买奖券中特等奖 C、明天会下雨 D、打开电视,正在播放动画片2. 如图,点A、B、C在⊙O上,若 , 则的度数为( )
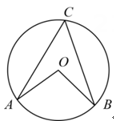 A、34° B、42° C、54° D、68°3. 已知⊙O的半径为5cm , 点A到圆心O的距离为6cm , 则点A与⊙O的位置关系为( )A、点A在⊙O上 B、点A在⊙O内 C、点A在⊙O外 D、不能确定4. 若一个正多边形的每个外角都是36°,则这个正多边形的边数是( )A、9 B、10 C、11 D、125. 如图,四边形ABCD内接于⊙O , 若∠B=108°,则∠D的度数为( )
A、34° B、42° C、54° D、68°3. 已知⊙O的半径为5cm , 点A到圆心O的距离为6cm , 则点A与⊙O的位置关系为( )A、点A在⊙O上 B、点A在⊙O内 C、点A在⊙O外 D、不能确定4. 若一个正多边形的每个外角都是36°,则这个正多边形的边数是( )A、9 B、10 C、11 D、125. 如图,四边形ABCD内接于⊙O , 若∠B=108°,则∠D的度数为( ) A、34° B、42° C、54° D、72°6. 已知扇形的圆心角为120°,面积为 , 则扇形的弧长是( )A、 B、 C、 D、7. 如图,在△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A′B′C , 点A的对应点A′落在AB边上,则∠BCA′的度数为( )
A、34° B、42° C、54° D、72°6. 已知扇形的圆心角为120°,面积为 , 则扇形的弧长是( )A、 B、 C、 D、7. 如图,在△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A′B′C , 点A的对应点A′落在AB边上,则∠BCA′的度数为( )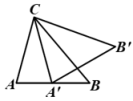 A、25° B、27.5° C、30° D、358. 如图,AB、CD是⊙O的两条直径,点E是劣弧的中点,连接BC,DE.若 , 则的度数为( )
A、25° B、27.5° C、30° D、358. 如图,AB、CD是⊙O的两条直径,点E是劣弧的中点,连接BC,DE.若 , 则的度数为( ) A、34° B、29° C、32° D、24°9. 已知函数y=-x2+2x+3,在a≤x≤4上最大值为4,最小值为-5,则a的取值范围是( )A、a≤-2 B、1≤a≤4 C、-2≤a≤1 D、a≥410. 如图,等腰三角形ABC内接于半圆O , AB=AC= , 半径长为 , 且直径EF∥BC , 则BC的长为( )
A、34° B、29° C、32° D、24°9. 已知函数y=-x2+2x+3,在a≤x≤4上最大值为4,最小值为-5,则a的取值范围是( )A、a≤-2 B、1≤a≤4 C、-2≤a≤1 D、a≥410. 如图,等腰三角形ABC内接于半圆O , AB=AC= , 半径长为 , 且直径EF∥BC , 则BC的长为( )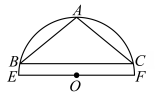 A、2 B、4 C、2 D、2
A、2 B、4 C、2 D、2二、填空题(本题有6小题,每小题4分,共24分)
-
11. 二次函数y=-2(x-1)2+4,图象的顶点坐标是 .12. 在一个不透明的盒子里装有5个黑色棋子和若干白棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是 , 则白色棋子的个数为 .13. 将二次函数y=x2-1的图象向上平移个单位,可以得到二次函数y=x2+2的图象.14. 同一平面内,一个点到圆的最小距离为6cm , 最大距离为8cm , 则该圆的半径为 .15. 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A , B , C , D分别是“果圆”与坐标轴的交点,抛物线的表达式为y=x2-2x-6,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为 .
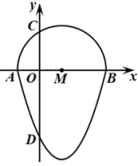 16. 如图,在△ABC中,∠ACB= , AB=10,BC=6,P是边AC上的动点,将线段BP绕点B按逆时针方向旋转到 , 旋转角等于∠ABC , 连结 .
16. 如图,在△ABC中,∠ACB= , AB=10,BC=6,P是边AC上的动点,将线段BP绕点B按逆时针方向旋转到 , 旋转角等于∠ABC , 连结 . (1)、当 , C , P在一条直线上时,线段AP的长是 .(2)、线段的最小值是 .
(1)、当 , C , P在一条直线上时,线段AP的长是 .(2)、线段的最小值是 .三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)
-
17. 如图,以△OAB的顶点O为圆心的⊙O交AB于点C , D , 且AC=BD , OA与OB相等吗?说明理由.
 18. 如图.在⊙O中.弦BC垂直于半径OA . 垂足为E . D是优弧上一点.连接BD、AD、OC , ∠ADB=30°。
18. 如图.在⊙O中.弦BC垂直于半径OA . 垂足为E . D是优弧上一点.连接BD、AD、OC , ∠ADB=30°。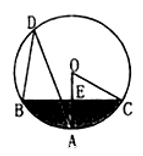 (1)、求∠AOC的度教;(2)、若弦BC= . 求图中阴影部分的面积。19. 已知二次函数y=x2+bx-5的图象经过点(2,7).(1)、求这个二次函数的表达式;(2)、求这个二次函数图象与x轴的交点坐标.20. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。21. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系.
(1)、求∠AOC的度教;(2)、若弦BC= . 求图中阴影部分的面积。19. 已知二次函数y=x2+bx-5的图象经过点(2,7).(1)、求这个二次函数的表达式;(2)、求这个二次函数图象与x轴的交点坐标.20. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y。(1)、用列表法或画树状图法,列出点M(x,y)的所有可能结果。(2)、求点M(x,y)在反比例函数y= 的图象上的概率。21. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系. (1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标;(3)、求四边形AOA1B1的面积.22. 一条盘水管的截面如图所示,水面宽AB垂直平分半径OD .
(1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标;(3)、求四边形AOA1B1的面积.22. 一条盘水管的截面如图所示,水面宽AB垂直平分半径OD . (1)、求∠ODB的度数;(2)、若⊙O的半径为6,求弦AB的长.(3)、若连结AD , 请判断四边形AOBD的形状,并给出证明.23. 一淘宝网店经营一种玩具,购进时的单价是30元.根据市场调查表明:当销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售
(1)、求∠ODB的度数;(2)、若⊙O的半径为6,求弦AB的长.(3)、若连结AD , 请判断四边形AOBD的形状,并给出证明.23. 一淘宝网店经营一种玩具,购进时的单价是30元.根据市场调查表明:当销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该玩具获得利润w元,并把结果填写在表格中:
销售单价(元
x
销售量(件
销售玩具获得利润w(元
(2)、若该网店要获得了10000元销售利润,求该玩具销售单价x应定为多少元?(3)、若该网店要完成不少于550件的销售任务,求网店销售该品牌玩具获得的最大利润是多少?
24. 如图,二次函数的图象与x轴相交于点A(-1,0)和B(m , 0),与y轴相交于点C , 且经过点D(3,3),过点D作DE⊥BD , 交y轴于点E , 连结BE . (1)、当m=6时,求这个二次函数的表达式.(2)、试用含m的代数式表示点C的坐标.(3)、作点D关于BE的对称点D′ , 连结OD′ , ED′ . 当△OD′E的面积等于1时,请直接写出m的值.
(1)、当m=6时,求这个二次函数的表达式.(2)、试用含m的代数式表示点C的坐标.(3)、作点D关于BE的对称点D′ , 连结OD′ , ED′ . 当△OD′E的面积等于1时,请直接写出m的值.