天津市武清区2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合要求的.请将正确选项填在下表中)
-
1. 在△ABC中,已知AC=3,BC=4,则AB的取值范围是( )A、6<AB<8 B、1<AB<7 C、2<AB<14 D、1<AB<142. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°4. 下列各图中,作出△ABC的AC边上的高,正确的是( )A、
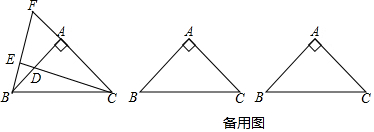
3. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°4. 下列各图中,作出△ABC的AC边上的高,正确的是( )A、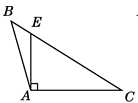 B、
B、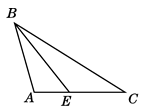 C、
C、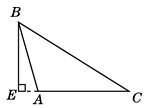 D、
D、 5. 若一个多边形的内角和与外角和相等,则这个多边形的边数是( )A、3 B、4 C、5 D、66. 下列选项中表示两个全等的图形的是( )A、形状相同的两个图形 B、周长相等的两个图形 C、面积相等的两个图形 D、能够完全重合的两个图形7. 如图,与相交于点 , , 要使≌ , 则需添加的一个条件可以是( )
5. 若一个多边形的内角和与外角和相等,则这个多边形的边数是( )A、3 B、4 C、5 D、66. 下列选项中表示两个全等的图形的是( )A、形状相同的两个图形 B、周长相等的两个图形 C、面积相等的两个图形 D、能够完全重合的两个图形7. 如图,与相交于点 , , 要使≌ , 则需添加的一个条件可以是( )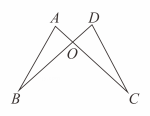 A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,AD平分∠BAC , 过点D作DE⊥AB , 若BC=7,BD=4,则DE的长为( )
A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,AD平分∠BAC , 过点D作DE⊥AB , 若BC=7,BD=4,则DE的长为( ) A、5 B、4 C、3 D、29. 等腰三角形的两条边长分别为15和7,则它的周长等于( )A、22 B、29 C、37 D、29或3710. 若点A(x,3)与点B(2,y)关于x轴对称,则( )A、x=﹣2,y=3 B、x=2,y=3 C、x=﹣2,y=﹣3 D、x=2,y=﹣311. 如图,在△ABC中,∠ACB=90°,CD⊥AB , 垂足为D , 若∠A=30°,BD=1,则AD的长为( )
A、5 B、4 C、3 D、29. 等腰三角形的两条边长分别为15和7,则它的周长等于( )A、22 B、29 C、37 D、29或3710. 若点A(x,3)与点B(2,y)关于x轴对称,则( )A、x=﹣2,y=3 B、x=2,y=3 C、x=﹣2,y=﹣3 D、x=2,y=﹣311. 如图,在△ABC中,∠ACB=90°,CD⊥AB , 垂足为D , 若∠A=30°,BD=1,则AD的长为( ) A、
A、 B、2
C、3
D、2
B、2
C、3
D、2 12. 如图,在 中, 是高, 是中线, 是角平分线, 交 于点G,交 于点H,下面说法正确的是( )
12. 如图,在 中, 是高, 是中线, 是角平分线, 交 于点G,交 于点H,下面说法正确的是( )
① 的面积 的面积 ② ; ③ ④ .
A、①②③④ B、①②④ C、①②③ D、③④二、填空题(本大题共6小题,每小题3分,共18分.请将答案直接填在题中横线上)
-
13. 已知等腰三角形的一个内角为110°,则等腰三角形的底角的度数为.14. 长度分别为2cm , 3cm , 7cm的木条 (填“能”或“不能”)围成一个三角形.15. 已知△ABC和△DEF中,AB=DE , BC=EF , 再添加一个条件可使△ABC≌△DEF , 则添加的条件为 .16. 如图,在△ABC中,AB=AC , AD=BD , ∠A=36°,则图中等腰三角形的个数是 .
 17. 如图,已知∠B+∠C=150°,则∠A+∠D+∠E+∠F等于 (度).
17. 如图,已知∠B+∠C=150°,则∠A+∠D+∠E+∠F等于 (度). 18. 如图,在3×3的正方形网格中,图中的△ABC为格点三角形.
18. 如图,在3×3的正方形网格中,图中的△ABC为格点三角形. (1)、在图中画出一个与△ABC成轴对称的格点三角形(画出一个即可);(2)、在图中与△ABC成轴对称的格点三角形共可画出 个.
(1)、在图中画出一个与△ABC成轴对称的格点三角形(画出一个即可);(2)、在图中与△ABC成轴对称的格点三角形共可画出 个.三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程)
-
19. 图中有几个三角形?用符号表示这些三角形.
 20. 如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
20. 如图,在平面直角坐标系中,△ABC的三个顶点均在格点上. (1)、写出△ABC三个顶点的坐标;(2)、画出△ABC关于y轴的对称图形△DEF , 点A , B , C的对应点分别是点D , E , F;(3)、写出(2)中△DEF三个顶点的坐标.21. 如图,有一池塘,要测池塘两端A , B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使CD=CA . 连接BC并延长到E , 使EC=CB , 连接DE .
(1)、写出△ABC三个顶点的坐标;(2)、画出△ABC关于y轴的对称图形△DEF , 点A , B , C的对应点分别是点D , E , F;(3)、写出(2)中△DEF三个顶点的坐标.21. 如图,有一池塘,要测池塘两端A , B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使CD=CA . 连接BC并延长到E , 使EC=CB , 连接DE . (1)、要测池塘两端A , B的距离,只要测出图中线段 的长即可;(2)、证明(1)中结论.22. 如图,在等边三角形ABC中,点D , E , F分别在边BC , CA , AB上,且AE=CD=BF .
(1)、要测池塘两端A , B的距离,只要测出图中线段 的长即可;(2)、证明(1)中结论.22. 如图,在等边三角形ABC中,点D , E , F分别在边BC , CA , AB上,且AE=CD=BF . (1)、判断△DEF的形状;(2)、证明(1)中结论.23. 如图,在△ABC与中,AC与BD相交于点E , 且∠A=∠D , AB=DC .
(1)、判断△DEF的形状;(2)、证明(1)中结论.23. 如图,在△ABC与中,AC与BD相交于点E , 且∠A=∠D , AB=DC . (1)、求证:△ABE≌△DCE;(2)、当∠AEB=50°时,求∠EBC的度数.
(1)、求证:△ABE≌△DCE;(2)、当∠AEB=50°时,求∠EBC的度数.