云南省文山州丘北县2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 下列是一元二次方程的是（）

A、x+y＝1 B、x²+2＝0 C、2x²-y＝1 D、 $x^{2} + \frac{1}{x} = 1$

查看试题解析
2. 下列图形中不一定是相似图形的是（　　）

A、两个等边三角形 B、两个等腰直角三角形 C、两个长方形 D、两个正方形

查看试题解析
3. 下列说法中，不正确的是（）

A、一组邻边相等的矩形是正方形 B、一组对边相等且有一个角是直角的四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
4. 连续掷两枚质地均匀的硬币，出现一枚正面朝上、一枚反面朝上的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、1

查看试题解析
5. 关于x的一元二次方程x²+（k-3）x-2k＝0的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定

查看试题解析
6. 一个盒子中装有a个白球和3个红球（除颜色外完全相同），若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在80%左右，则a的值约为（）

A、9 B、12 C、15 D、18

查看试题解析
7. 在一幅比例尺为1：1000000的地图上，量得某座大桥长5.5厘米，这座大桥的实际长度是（）

A、55米 B、10千米 C、55千米

查看试题解析
8. 如图，将矩形ABCD绕点A旋转一个角度得到AB₁C₁D₁ ，使得点D₁恰好落在BC边上，若AD＝2AB＝4，则CD₁的长为（）

A、1 B、2 C、 $2 \sqrt{3}$ D、 $4 - 2 \sqrt{3}$

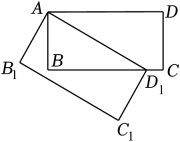查看试题解析
9. 若a、b是菱形ABCD的两条对角线的长，且a、b是一元二次方程x²-14x+48＝0的两个根，则菱形ABCD的边长为（）

A、4 B、5 C、 $\sqrt{13}$ D、10

查看试题解析
10. 如图，点 $D$ 在 $△ A B C$ 的边 $A C$ 上，添加一个条件，不能判断 $△ A B C$ 与 $△ B D C$ 相似的是（）

A、 $∠ C B D = ∠ A$ B、 $\frac{B C}{A C} = \frac{C D}{A B}$ C、 $∠ C B A = ∠ C D B$ D、 $\frac{B C}{A C} = \frac{C D}{B C} = \frac{D B}{A B}$

查看试题解析
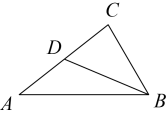11. 要组织一次篮球邀请赛，参赛的每两个队之间都要赛一场，赛程计划安排7天，每天安排4场比赛．如果共有x个队参赛，为了求出x ，根据题意可列方程（）

A、x（x+1）＝4×7 B、x（x-1）＝4×7 C、 $\frac{1}{2} x (x + 1) = 4 \times 7$ D、 $\frac{1}{2} x (x - 1) = 4 \times 7$

查看试题解析
12. 如图，在正方形ABCD中，E、F、H分别是AB、BC、CD的中点，CE、DF交于点G ，连接AG ，下列结论中，不正确的是（）

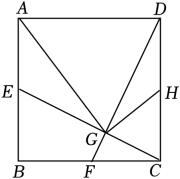A、CE＝DF B、CE⊥DF C、 $G H = \frac{1}{2} A D$ D、△ADG是等边三角形

查看试题解析

二、填空题（本大题共4小题，每小题2分共8分）

13. 如果 $\frac{b}{a - b} = \frac{3}{2}$ ，那么 $\frac{a}{b}$ ＝．

查看试题解析
14. 如图，在△ABC中，若∠ACB＝90°，点D是AB的中点，AB＝4，则CD的长度是．

查看试题解析
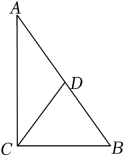15. 若关于x的方程x²+bx+6＝0的一个根是3，则b的值为．

查看试题解析
16. 如图，在菱形ABCD中，对角线AC ， BD相交于点O ，点E为CD的中点．若OE＝3，则菱形ABCD的周长为．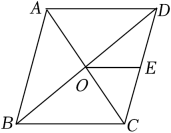

查看试题解析

三、解答题（本大题共8小题，共56分）

17. 解方程：

(1)、x²-4x＝4；

(2)、（x+2）（x+1）＝12．

查看试题解析
18. 如图，D、E、F分别是△ABC的AB、AC、BC边上的点，且DE∥BC ， EF∥AB ，求证：△ADE∽△EFC ．

查看试题解析
19. 随着“共享经济”的概念迅速普及，共享汽车业进入了人们的视野，某共享汽车租赁公司年初在某地投放了一批共享汽车，全天包车的租金定为每辆120元．据统计，八月份的全天包车数为25次，在租金不变的基础下，九月、十月的全天包车数持续走高，十月份的全天包车数达到64次．若从八月份到十月份的全天包车数月平均增长率不变，求全天包车数的月平均增长率．

查看试题解析
20. 如图，佳佳同学正在使用手电筒进行物理光学实验，水平地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F ，落在墙上的点E处，点E到地面的高度DE＝3.5m ，点F到地面的高度CF＝1.5m ，灯泡到木板的水平距离AC＝5.4m ，木板到平面镜的水平距离BC＝3m ，已知光在镜面反射中的入射角等于反射角，求灯泡到地面的高度AG ．

查看试题解析
21. 在一个不透明的袋子中装有3个大小、质地完全相同的乒乓球，球面上分别标有数字1、2、3，搅匀后先从袋子中任意摸出一个乒乓球，记下数字后放回，搅匀后再从袋子中任意摸出一个乒乓球，记下数字．

(1)、用列表或画树状图的方法表示出所有可能出现的结果；

(2)、求两次摸到乒乓球上的数字之和是奇数的概率．

查看试题解析
22. 如图，在四边形ABCD中，AB∥DC ， AB＝CD ，对角线AC、BD交于点O ，过点C作CE⊥AB交AB延长线于点E ，且∠ABO＝∠ACE ，连接OE ．

(1)、求证：四边形ABCD是菱形；

(2)、若 $C E = 3 \sqrt{3}$ ， ∠ADC＝120°，求菱形ABCD的面积．

查看试题解析
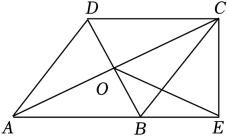23. 已知实数a、b满足（2a²+b²+1）（2a²+b²-1）＝80，试求2a²+b²的值．解：设2a²+b²＝m ，则原方程可化为（m+1）（m-1）＝80，即m²＝81，解得：m＝±9，∵2a²+b²≥0，∴2a²+b²＝9，上面的这种方法称为“换元法”，换元法是数学学习中最常用的一种思想方法，在结构较复杂的数和式的运算中，若把其中某些部分看成一个整体，并用新字母代替（即换元），则能使复杂问题简单化．根据以上阅读材料，解决下列问题：

(1)、已知实数x、y满足（2x²+2y²-1）（x²+y²）＝3，求3x²+3y²-2的值；

(2)、若四个连续正整数的积为120，求这四个正整数．

查看试题解析
24. 如图，在四边形ABCD中，对角线AC、BD相交于点O ， OA＝OC ， OB＝OD ， ∠ABC＝90°，AB＝6cm ， BC＝12cm ，动点P从点A出发沿着边AB向点B以1cm/s的速度运动，同时动点Q从点B出发沿着边BC向点C以2cm/s的速度运动，当点P停止运动时，点Q也随之停止运动，设运动时间为ts ．

(1)、求证：四边形ABCD是矩形；

(2)、是否存在某一时刻，使得以B、P、Q为顶点的三角形与△ABC相似？若存在，求出此时t的值；若不存在，请说明理由．

查看试题解析