北京市四十四中2023-2024学年八年级上学期数学月考考试试卷
试卷更新日期:2023-11-24 类型:月考试卷
一、选择题(每小题4分,共32分)
-
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑、白棋子摆成的图案中.是轴对称图形的是( )A、
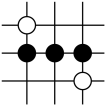 B、
B、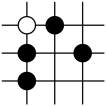 C、
C、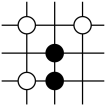 D、
D、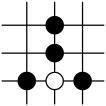 2. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
2. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )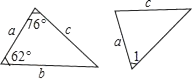 A、76° B、62° C、42° D、76°、62°或42°都可以3. 如图是战机在空中展示的轴对称队形.以飞机B , C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
A、76° B、62° C、42° D、76°、62°或42°都可以3. 如图是战机在空中展示的轴对称队形.以飞机B , C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )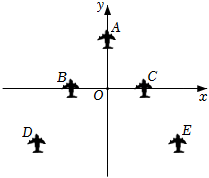 A、(40,-a) B、(-40,a) C、(-40,-a) D、(a , -40)4. 如图,在△ABC和△ABD中,已知∠CAB=∠DAB , 在不添加任何辅助线的前提下,要使△ABC≌△ABD , 只需再添加的一个条件不可以是( )
A、(40,-a) B、(-40,a) C、(-40,-a) D、(a , -40)4. 如图,在△ABC和△ABD中,已知∠CAB=∠DAB , 在不添加任何辅助线的前提下,要使△ABC≌△ABD , 只需再添加的一个条件不可以是( )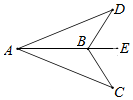 A、AC=AD B、BC=BD C、∠C=∠D D、∠CBE=∠DBE5. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、AC=AD B、BC=BD C、∠C=∠D D、∠CBE=∠DBE5. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )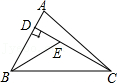 A、10 B、7 C、5 D、46. 如图,已知∠A=60°,∠B=40°,∠C=30°,则∠D+∠E等于( )
A、10 B、7 C、5 D、46. 如图,已知∠A=60°,∠B=40°,∠C=30°,则∠D+∠E等于( )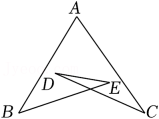 A、30° B、40° C、50° D、60°7. 如图,PD垂直平分AB , PE垂直平分BC , 若PA的长为7,则PC的长为( )
A、30° B、40° C、50° D、60°7. 如图,PD垂直平分AB , PE垂直平分BC , 若PA的长为7,则PC的长为( )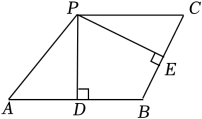 A、5 B、6 C、7 D、88. 如图,在Rt△ABC中,AC=6,BC=8,AB=10.点P从点A出发,以每秒2个单位长度的速度沿折线A-C-B向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线B-C-A向终点A运动,点P , Q都运动到各自的终点时停止.设运动时间为t(秒),直线l经过点C , 且l∥AB , 过点P , Q分别作直线l的垂线段,垂足为E , F . 当△CPE与△CQF全等时,t的值不可能是( )
A、5 B、6 C、7 D、88. 如图,在Rt△ABC中,AC=6,BC=8,AB=10.点P从点A出发,以每秒2个单位长度的速度沿折线A-C-B向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线B-C-A向终点A运动,点P , Q都运动到各自的终点时停止.设运动时间为t(秒),直线l经过点C , 且l∥AB , 过点P , Q分别作直线l的垂线段,垂足为E , F . 当△CPE与△CQF全等时,t的值不可能是( )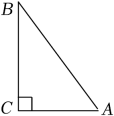 A、2 B、2.8 C、3 D、6
A、2 B、2.8 C、3 D、6二、填空题(每小题3分,共24分)
-
9. 如图,公园里有一座假山,要测量假山两端A、B的距离,先在平地上取一个可以直接到达A、B的点C , 分别延长AC、BC , 到D、E , 使CE=CB , CA=CD , 连接DE , 这样就可以利用三角形全等,通过测量DE的长得到假山两端A、B的距离,则这两个三角形全等的依据是 .
 10. 在9×7的网格中,∠AOB的位置如图所示,则到∠AOB两边距离相等的点是 .
10. 在9×7的网格中,∠AOB的位置如图所示,则到∠AOB两边距离相等的点是 .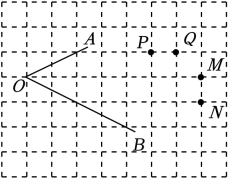 11. 图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=度.
11. 图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=度. 12. 如图所示,在△ABC中,∠B=∠C=50°,BD=CF , BE=CD , 则∠EDF的度数是 .
12. 如图所示,在△ABC中,∠B=∠C=50°,BD=CF , BE=CD , 则∠EDF的度数是 .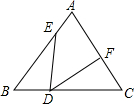 13. 如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB , BC于点D、E , AC的垂直平分线分别交AC , BC于点F、G , 则△AEG的周长为 .
13. 如图,在△ABC中,AB=6,AC=8,BC=11,AB的垂直平分线分别交AB , BC于点D、E , AC的垂直平分线分别交AC , BC于点F、G , 则△AEG的周长为 .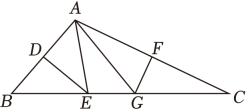 14. 如图,在△ABC中,∠B=40°,∠C=30°,D为边BC上一点,将△ADC沿直线AD翻折后,点C落到点E处.若DE∥AB , 则∠AFC的度数为 .
14. 如图,在△ABC中,∠B=40°,∠C=30°,D为边BC上一点,将△ADC沿直线AD翻折后,点C落到点E处.若DE∥AB , 则∠AFC的度数为 . 15. 如图,在平面直角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A , B . 则OA+OB的长是 .
15. 如图,在平面直角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A , B . 则OA+OB的长是 .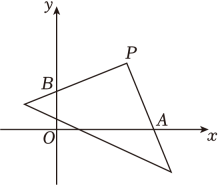 16. 李老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点Q在轨道槽AM上运A动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动.图2是操作学具时,所对应某个位置的图形的示意图.
16. 李老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题.操作学具时,点Q在轨道槽AM上运A动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动.图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ;
②当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ;
③当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ;
其中所有正确结论的序号是 .
三、解答题(共44分)
-
17. 下面是小东设计的尺规作图过程.
已知:如图,在Rt△ABC中,∠ABC=90°,
求作:点D , 使点D在BC边上,且到AB和AC的距离相等.
作法:①如图,以点A为圆心,任意长为半径画弧,分别交AB , AC于点M、N;
②分别以点M , N为圆心,大于
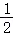 MN的长为半径画弧,两弧交于点P;
MN的长为半径画弧,两弧交于点P;③画射线AP , 交BC于点D .
所以点D即为所求.
根据小东设计的尺规作图过程:
(1)、使用直尺和圆规,补全图形(保留作图痕迹);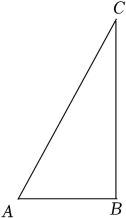 (2)、完成下面的证明.
(2)、完成下面的证明.证明:过点D作DE⊥AC于点E , 连接MP , NP .
在△AMP与△ANP中,
∵AM=AN , MP=NP , AP=AP ,
∴△AMP≌△ANP(SSS).
∴∠▲=∠▲ .
∵∠ABC=90°,
∴DB⊥AB .
又∵DE⊥AC ,
∴DB=DE( )(填推理的依据)
18. 如图,在△ABC中, (1)、尺规作图:作边AC的垂直平分线,交AB于点D,交AC于点E,连结CD.(2)、若△BCD的周长等于18,AE=4,求△ABC的周长.19. 如图,在四边形ABCD中,已知AD∥BC , E为CD的中点,连接AE并延长AE交BC的延长线于点F .
(1)、尺规作图:作边AC的垂直平分线,交AB于点D,交AC于点E,连结CD.(2)、若△BCD的周长等于18,AE=4,求△ABC的周长.19. 如图,在四边形ABCD中,已知AD∥BC , E为CD的中点,连接AE并延长AE交BC的延长线于点F .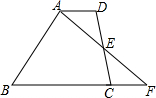 (1)、求证:CF=AD;(2)、若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上?为什么?20. 如图,四边形ABCD中,AB=AD , BC=DC , 我们把这种两组邻边分别相等的四边形叫做“筝形”.
(1)、求证:CF=AD;(2)、若AD=2,AB=8,当BC为多少时,点B在线段AF的垂直平分线上?为什么?20. 如图,四边形ABCD中,AB=AD , BC=DC , 我们把这种两组邻边分别相等的四边形叫做“筝形”.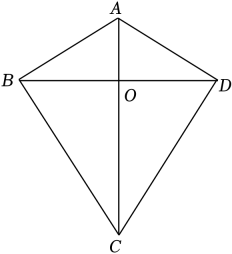 (1)、求证:△ABC≌△ADC;(2)、测量OB与OD、∠BOA与∠DOA , 你有何猜想?证明你的猜想.
(1)、求证:△ABC≌△ADC;(2)、测量OB与OD、∠BOA与∠DOA , 你有何猜想?证明你的猜想.

