山东省济南市商河县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-11-24 类型:期中考试
一、单选题(4*10)
-
1. 一个几何体如图水平放置,它的俯视图是( )
 A、
A、 B、
B、 C、
C、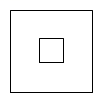 D、
D、 2. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、33. 菱形不一定具有的性质是( )A、四条边相等 B、对角线相等 C、是轴对称图形 D、是中心对称图形4. 如图,直线 , 直线AC和DF被 , , 所截,AB=8,BC=12,EF=9,则DE的长为( )
2. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、33. 菱形不一定具有的性质是( )A、四条边相等 B、对角线相等 C、是轴对称图形 D、是中心对称图形4. 如图,直线 , 直线AC和DF被 , , 所截,AB=8,BC=12,EF=9,则DE的长为( ) A、5 B、6 C、7 D、85. 一元二次方程经过配方后,可变形为 ( )A、 B、 C、 D、6. 已知与△相似,且相似比为 , 则与△的面积比为A、1:1 B、1:3 C、1:6 D、1:97. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、8. 一本书的宽与长之比为黄金比,书的长为14cm,则它的宽为( )cmA、 B、 C、 D、9. 如图,矩形内接于 , 且边落在上,若 , , , , 那么的长为( )
A、5 B、6 C、7 D、85. 一元二次方程经过配方后,可变形为 ( )A、 B、 C、 D、6. 已知与△相似,且相似比为 , 则与△的面积比为A、1:1 B、1:3 C、1:6 D、1:97. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、8. 一本书的宽与长之比为黄金比,书的长为14cm,则它的宽为( )cmA、 B、 C、 D、9. 如图,矩形内接于 , 且边落在上,若 , , , , 那么的长为( ) A、 B、 C、 D、10. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( )
A、 B、 C、 D、10. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(6*4)
-
11. 若 ,则 = .12. 关于 的一元二次方程 的一个根是2,则另一个根是 .13. 在平面直角坐标系中,已知点 , , 以原点为位似中心,画 , 使它与位似,且相似比为 , 则点的对应点的坐标是 .14. 若关于的一元二次方程有实数根,则实数的取值范围是 .15. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为.
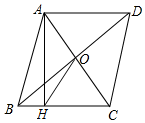 16. 如图,E , F是平行四边形对角线上两点, , 连接并延长,分别交于点G , H , 连接 , 下列结论:① , ② , ③ , ④ , 其中正确的结论有(只填序号).
16. 如图,E , F是平行四边形对角线上两点, , 连接并延长,分别交于点G , H , 连接 , 下列结论:① , ② , ③ , ④ , 其中正确的结论有(只填序号).
三、解答题
-
17. 解方程:(1)、(2)、18. 如图,在平行四边形ABCD中,点E , F在上, . 求证: .
 19. 为了测得一棵树的高度 , 一个小组的同学进行了如下测量:在阳光下,测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时发现这棵树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),测得墙壁上的影长为1.5米,落在地面上的影长为3米.
19. 为了测得一棵树的高度 , 一个小组的同学进行了如下测量:在阳光下,测得一根与地面垂直、长为1米的竹竿的影长为0.8米.同时发现这棵树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),测得墙壁上的影长为1.5米,落在地面上的影长为3米.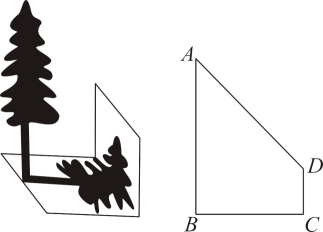 (1)、该小组同学是利用投影的有关知识进行计算的;(填“平行”或“中心”)(2)、求这棵树的高度 .20. 李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有:A.转移注意力,B.合理宣泄,C.自我暗示,D.放松训练.(1)、若小如随机取走一个锦囊,则取走的是写有“自我暗示”的概率是;(2)、若小如和小意每人先后随机抽取一个锦囊(取走后不放回),请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的概率.21. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
(1)、该小组同学是利用投影的有关知识进行计算的;(填“平行”或“中心”)(2)、求这棵树的高度 .20. 李老师为缓解小如和小意的压力,准备了四个完全相同(不透明)的锦囊,里面各装有一张纸条,分别写有:A.转移注意力,B.合理宣泄,C.自我暗示,D.放松训练.(1)、若小如随机取走一个锦囊,则取走的是写有“自我暗示”的概率是;(2)、若小如和小意每人先后随机抽取一个锦囊(取走后不放回),请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的概率.21. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP. 22. 如图,用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),若这个围栏的面积为 , 求与墙垂直的一边的长度.
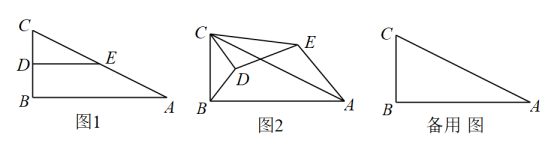
22. 如图,用一段长为的篱笆围成一个一边靠墙的矩形围栏(墙长),若这个围栏的面积为 , 求与墙垂直的一边的长度. 23. 如图,、相交于点 , 连接、 , 且 , , , , 求的长.
23. 如图,、相交于点 , 连接、 , 且 , , , , 求的长.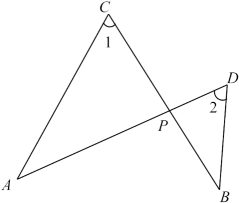 24. 某公司设计了一款工艺品,每件的成本是40元,为了合理定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件52元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?
24. 某公司设计了一款工艺品,每件的成本是40元,为了合理定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件52元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?