湖南省长沙市长郡教育集团2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本大题共10个小题,每小题3分,共30分,在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项)
-
1. 我们生活在一个充满对称的世界中:许多建筑都设计成对称形,艺术作品的创作往往也从对称角度考虑,自然界的许多动植物也按对称形生长,中国的方块字中有些也具有对称性……对称给我们带来多少美的感受!在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中,轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 小明和小红两位小朋友在做拼三角形的游戏,小明手上有两根木棒长分别为和 , 小红手上有四根木棒,长度如下: , , , , 小明从小红手中选一根要能拼成一个三角形的木棒,小明应选的木棒长度是( )A、 B、 C、 D、3. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
2. 小明和小红两位小朋友在做拼三角形的游戏,小明手上有两根木棒长分别为和 , 小红手上有四根木棒,长度如下: , , , , 小明从小红手中选一根要能拼成一个三角形的木棒,小明应选的木棒长度是( )A、 B、 C、 D、3. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )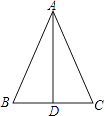 A、∠B=∠C B、AD⊥BC C、AD平分∠BAC D、AB=2BD6. 如图,在中,已知 , , 则的度数为( )
A、∠B=∠C B、AD⊥BC C、AD平分∠BAC D、AB=2BD6. 如图,在中,已知 , , 则的度数为( ) A、 B、 C、 D、7. 如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
A、 B、 C、 D、7. 如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( ) A、360° B、250° C、180° D、140°8. 如图,已知 , 添加下列一个条件后,无法判定的是( )
A、360° B、250° C、180° D、140°8. 如图,已知 , 添加下列一个条件后,无法判定的是( ) A、 B、 C、 D、9. 如果等腰三角形两边长是和 , 那么它的周长是( )A、 B、 C、 D、16或10. 如图,平分 , 于点 , 于点 , 连接交于点 , 则下列结论:①;②;③;④ , 其中正确结论的个数是( )
A、 B、 C、 D、9. 如果等腰三角形两边长是和 , 那么它的周长是( )A、 B、 C、 D、16或10. 如图,平分 , 于点 , 于点 , 连接交于点 , 则下列结论:①;②;③;④ , 其中正确结论的个数是( )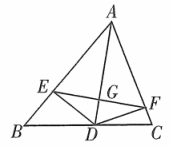 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本题共6个小题,每小题3分,共18分)
-
11. 已知 , , 则的值是 .12. 已知边形的内角和等于 , 则的值是 .13. 如图,已知线段是等边的高,点在上,且 , 则 .
 14. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交于点 , 连接 , 若 , , 则的周长为 .
14. 如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交于点 , 连接 , 若 , , 则的周长为 . 15. 如图,已知 , , , , 垂足点分别是 , , , , 则的长为 .
15. 如图,已知 , , , , 垂足点分别是 , , , , 则的长为 . 16. 如图,已知是的中线, , , 则线段的取值范围是 .
16. 如图,已知是的中线, , , 则线段的取值范围是 .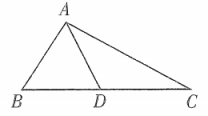
三、解答题(本题共8个小题,共72分)
-
17. 计算:(1)、;(2)、;(3)、;(4)、 .18. 先化简,再求值: , 其中 , .19. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点 , , 在小正方形的顶点上.
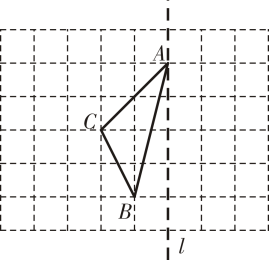
⑴在图中画出与关于直线成轴对称的;
⑵求的面积;
⑶在直线上找一点(在答题纸上图中标出),使的值最小.
20. 已知 , .(1)、求的值;(2)、求的值.21. 如图,已知在与中,与交于点 , 且 , . (1)、求证:;(2)、当时,求的度数.22. 如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,
(1)、求证:;(2)、当时,求的度数.22. 如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F, (1)、求∠F的度数;(2)、若CD=3,求DF的长.23. 阅读材料,解决后面的问题:
(1)、求∠F的度数;(2)、若CD=3,求DF的长.23. 阅读材料,解决后面的问题:若 , 求的值.
解: ,
,
即: , , ,
解得: , , .
(1)、若 , 求的值;(2)、已知等腰的两边长 , , 满足 , 求该的周长;(3)、已知正整数 , , 满足不等式 , 求的值.24. 如图1,在平面直角坐标系中,已知点 , , 且 , 满足 .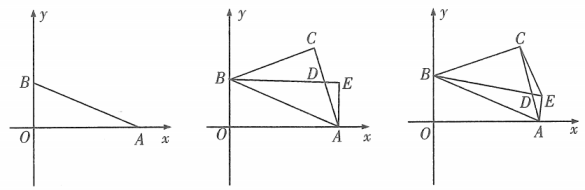
图1 图2 图3
(1)、求的面积;(2)、如图1,以为斜边构造等腰直角 , 请直接写出点的坐标;(3)、如图2,已知等腰直角中, , , 点是腰上的一点(不与 , 重合),连接 , 过点作 , 垂足为点 .①若是的角平分线,求证:;
②探究:如图3,连接 , 当点在线段上运动时(不与 , 重合),的大小是否发生变化?若改变,求出它的最大值;若不改变,求出这个定值.