河北省石家庄市栾城区2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题（本大题共12个小题，每小题2分，共24分，把每小题的正确选项填涂在答题纸上）

1. 下列函数关系式中属于反比例函数的是（）

A、 $y = 3 x$ B、 $y = - \frac{2}{x}$ C、 $y = x^{2} + 3$ D、 $x + y = 52$

查看试题解析
2. 把一元二次方程 $2 x (x - 1) = (x - 3) + 4$ 化成一般式之后，其二次项系数与一次项分别是（）

A、2， $- 3$ B、 $- 2$ ， $- 3$ C、2， $- 3 x$ D、 $- 2$ ， $- 3 x$

查看试题解析
3. 如图，在 $5 \times 6$ 的正方形网格中，点A ， B ， C都在格点上，则 $t a n ∠ A B C$ 的值为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、1 D、 $\frac{\sqrt{3}}{3}$

查看试题解析
4. 如图，在 $6 \times 6$ 的正方形网格中，以O为位似中心，把格点 $△ A B C$ 放大为原来的2倍，则A的对应点为（）

A、点 $A_{1}$ B、点 $A_{2}$ C、点 $A_{3}$ D、点 $A_{4}$

查看试题解析
5. 一组数据1，x，5，7有唯一众数，且中位数是6，则平均数是（）

A、6 B、5 C、4 D、3

查看试题解析
6. 某射击运动队进行了五次射击测试，甲、乙两名选手的测试成绩如下表．甲、乙两名选手成绩的方差分别记为 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ ，则 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ 的大小关系是（）

A、 $S_{甲}^{2} > S_{乙}^{2}$ B、 $S_{甲}^{2} < S_{乙}^{2}$ C、 $S_{单}^{2} = S_{乙}^{2}$ D、无法确定

查看试题解析
7. 下列关于x的一元二次方程中有两个不相等的实数根的方程是（）

A、 $x^{2} + 1 = 0$ B、 $x^{2} + x - 1 = 0$ C、 $2 x^{2} + 2 x + 3 = 0$ D、 $4 x^{2} - 4 x + 1 = 0$

查看试题解析
8. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
9. 在人体躯干与身高的比例上，肚脐是理想的黄金分割点，即脚底到肚脐的长度与身高的比值越接近0.618越给人以美感．小明的妈妈脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该穿多高的高跟鞋看起来会更美？（）

A、0.075m B、0.8m C、0.085m D、0.065m

查看试题解析
10. 反比例函数 $y = \frac{k}{x}$ 的图象经过 $A (3 ， m)$ 、 $B (m - 1 ， 6)$ 两点，则k的值为（）

A、4 B、6 C、9 D、12

查看试题解析
11. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ，点D在 $A C$ 上， $∠ D B C = ∠ A$ ．若 $A C = 4 ， c o s A = \frac{4}{5}$ ，则 $B D$ 的长度为（）

A、 $\frac{9}{4}$ B、 $\frac{12}{5}$ C、 $\frac{15}{4}$ D、4

查看试题解析
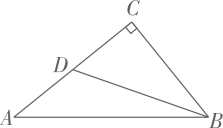12. 如图，在锐角三角形ABC中， $A B = 6$ cm， $A C = 12$ cm，动点D从点A出发到点B停止，动点E从点C出发到点A停止，点D运动的速度为1cm/s，点E运动的速度为2cm/s，如果两点同时开始运动，那么以点A ， D ， E为顶点的三角形与 $△ A B C$ 相似时的运动时间为（）

A、4.5s或3s B、3s C、4.5s D、4.8s或3s

查看试题解析

二、填空题（本大题共8个小题，每小题3分，共24分，将正确答案填写在答题纸上）

13. 已知一组数据：4，5，5，6，5，4，7，8，则这组数据的众数是.

查看试题解析
14. 如图，矩形ABCD的边AB与y轴平行，顶点A的坐标为 $(1 ， 4)$ ，顶点C的坐标为 $(3 ， 1)$ ，若反比例函数 $y = \frac{k}{x}$ 的图像与矩形ABCD有公共点，则k的值可以是．（写出一个即可）

查看试题解析
15. “共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献．全球共有40多个国家引种杂交水稻，中国境外种植面积达800万公顷．某村引进了甲、乙两种超级杂交水稻品种，在条件（肥力、日照、通风……）不同的6块试验田中同时播种并核定亩产，统计结果为： ${\bar{x}}_{甲} = 1042$ kg/亩， $s_{甲}^{2} = 6.5$ ， $\bar{x} /_{乙} = 1042$ kg/亩， $s_{乙}^{2} = 1.2$ ，则品种更适合在该村推广．（填“甲”或“乙”）

查看试题解析
16. 方程 $x^{2} + m x - 1 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，且 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 3$ ，则 $m =$ ．

查看试题解析
17. 某楼盘2020年房价为每平方米8100元，经过两年连续降价后，2022年房价为7600元．设该楼盘这两年房价平均降低率为x ，根据题意可列方程为．

查看试题解析
18. 如图 $△ A B C$ 中， $A B = A C$ ，点D ， E分别是边AB ， AC的中点，点G ， F在BC边上，四边形DEFG是正方形．若 $D E = 2$ cm，则 $A C =$ cm．

查看试题解析
19. 如图，在矩形 $A B C D$ 中， $D E ⊥ A C$ ，垂足为点 $E$ .若 $\sin ∠ A D E = \frac{4}{5}$ ， $A D = 4$ ，则 $A B$ 的长为.

查看试题解析
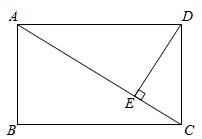20. 如图，在平行四边形ABCD中，E是线段AB上一点，连结AC、DE交于点F．若 $\frac{A E}{E B} = \frac{2}{3}$ ，则 $\frac{S_{△ A D F}}{S_{△ A E F}} =$ ．

查看试题解析

三、解答题（本大题共5个小题，满分52分，解答应写出相应的文字说明、证明过程或演算步骤，将答案写在答题纸上）

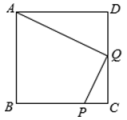
21. 如图，利用一面墙（墙EF最长可利用28米），围成一个矩形花园ABCD ．与墙平行的一边BC上要预留2米宽的入口（如图中MN所示，不用砌墙）．用砌60米长的墙的材料，当矩形的长BC为多少米时，矩形花园的面积为300平方米；能否围成480平方米的矩形花园，为什么？

查看试题解析
22. 为了解学生完成书面作业所用时间的情况，进一步优化作业管理，某中学从全校学生中随机抽取部分学生，对他们一周平均每天完成书面作业的时间t（单位：分钟）进行调查．将调查数据进行整理后分为五组：A组“ $0 < t \leq 45$ ”；B组“ $45 < t \leq 60$ ”；C组“ $60 < t \leq 75$ ”；D组“ $75 < t \leq 90$ ”；E组“ $t > 90$ ”．现将调查结果绘制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：

(1)、这次调查的样本容量是，请补全条形统计图；

(2)、在扇形统计图中，A组对应的圆心角的度数是°，本次调查数据的中位数落在组内；

(3)、若该中学有2000名学生，请你估计该中学一周平均每天完成书面作业不超过90分钟的学生有多少人？

查看试题解析
23. 如图，它是反比例函数 $y = \frac{m - 1}{x}$ （m为常数，且 $m \neq 1$ ）图象的一支．

(1)、图象的另一支位于哪个象限？求m的取值范围；

(2)、点 $A (2 ， 3)$ 在该反比例函数的图象上．
①判断点 $B (3 ， 2)$ ， $C (4 ， - 2)$ ， $D (- 1 ， - 6)$ 是否在这个函数的图象上，并说明理由；
②在该函数图象的某一支上任取点 $M (x_{1} ， y_{1})$ 和 $N (x_{2} ， y_{2})$ ．如果 $x_{1} < x_{2}$ ，那么 $y_{1}$ 和 $y_{2}$ 有怎样的大小关系？

查看试题解析
24. 如图所示，在正方形ABCD中，P是BC上的点，且 $B P = 3 P C$ ， Q是CD的中点．

(1)、 $△ A D Q$ 与 $△ Q C P$ 是否相似？为什么？

(2)、试问：AQ与PQ有什么关系？

查看试题解析
25. 如图，某天然气公司的主输气管道途经A小区，继续沿A小区的北偏东60°方向往前铺设．测绘员在A处测得另一个需要安装天然气的P小区位于北偏东30°方向，测绘员从A处出发，沿主输气管道方向前行2000米
到达B处，此时测得P小区位于北偏西75°方向．

(1)、 $∠ P A B =$ 度， $∠ P B A =$ 度；

(2)、现要在主输气管道AB上选择一个支管道连接点Q ，使从Q处到P小区铺设的管道最短，求A小区与支管道连接点Q的距离．（结果保留根号）

查看试题解析