甘肃省白银市2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题．（每题只有一个正确答案，请将正确答案填在下面的表格里．每题3分，共36分）

1. 若 $a$ 是常数，下列方程中一定是一元二次方程的是（）

A、 $(a + 1) x^{2} + 5 x - 1 = 0$ B、 $(a^{2} - 1) x^{2} - 2 x + 3 = 0$ C、 $(a^{2} + 1) x^{2} + 2 x + 1 = 0$ D、 $(a - 1) x^{2} + 3 x + 1 = 0$

查看试题解析
2. 已知矩形 $A B C D$ 的对角线 $A C = 4 c m$ ，则 $B D =$ （）

A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $4 c m$

查看试题解析
3. 将一元二次方程 $x (x + 1) - 2 x = 2$ 化为一般形式，正确的是（）

A、 $x^{2} - x = 2$ B、 $x^{2} + x + 2 = 0$ C、 $x^{2} - x + 2 = 0$ D、 $x^{2} - x - 2 = 0$

查看试题解析
4. 具有四条边都相等的性质的四边形是（）

A、任意四边形 B、平行四边形 C、矩形 D、菱形

查看试题解析
5. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，并绘制了如下表格．则该结果发生的概率约为（）
实验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.345 0.339 0.333

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
6. 一元二次方程 $x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
7. 在Rt△ABC中，∠ACB=90°，∠B=30°，AC= $\sqrt{3}$ cm，则AB边上的中线为（　　）

A、1cm B、2cm C、1.5cm D、 $\sqrt{3}$ cm

查看试题解析
8. 若 $x = - 2$ 是一元二次方程 $x^{2} + 2 x + m = 0$ 的一个根，则方程的另一个根是（）

A、2 B、1 C、0 D、 $- 2$

查看试题解析
9. 2023年12月13日，是我国第十个南京大屠杀死难者国家公祭日．某地从《南京！南京！》《东京审判》《屠城血证》三部影片中随机选取两部进行展播，则恰好展播《南京！南京！》《东京审判》的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
10. 如图，已知 $▱ A B C D$ 的四个内角的平分线分别交于点 $E$ 、 $F$ 、 $G$ 、 $H$ ，则四边形 $E F G H$ 的形状是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
11. 某超市第一季度中，1月的营业额为200万元，2、3月的总营业额为1000万元，如果平均每月增长率为 $x$ ，由题意可列方程（）

A、 $200 {(1 + x)}^{2} = 1000$ B、 $200 + 200 \times 2 x = 1000$ C、 $200 (1 + x) + 200 {(1 + x)}^{2} = 1000$ D、 $200 + 200 (1 + x) + 200 {(1 + x)}^{2} = 1000$

查看试题解析
12. 如图，正方形ABCD的边长为4，E为BC上一点， $B E = 1$ ， F为AB上一点， $A F = 2$ ， P为AC上一点，则 $P F + P E$ 的最小值为（）

A、 $\sqrt{15}$ B、4 C、 $\sqrt{17}$ D、 $3 \sqrt{2}$

查看试题解析

二、填空题．（每题3分，共12分）

13. 方程 $x^{2} - 2 x = 0$ 的根为．

查看试题解析
14. 为了解某地南迁到该区域某湿地的A种候鸟的情况，从中捕捉40只，戴上识别卡并放回，经过一段时间后观察发现，200只A种候鸟只有10只戴着识别卡，由此可估计该湿地有只A种候鸟．

查看试题解析
15. 如图，矩形 $O A B C$ 的顶点 $A$ 在 $x$ 轴上，点 $B$ 的坐标为 $(1 ， 2)$ ，固定边 $O A$ ，向左“推”矩形 $O A B C$ 使点 $B$ 落在 $y$ 轴的点 $B^{'}$ 的位置，则点 $C$ 的对应点 $C^{'}$ 的坐标是．

查看试题解析
16. 在 $▱ A B C D$ 中， $A B = 10 ， B C = 14 ， E 、 F$ 分别为边 $B C 、 A D$ 上的点，若四边形 $A E C F$ 为正方形，则 $A E$ 的长为．

查看试题解析

三、解答题．（本大题12个小题，共72分）

17. 解方程： $x^{2} + 2 x - 2 = 0$ .

查看试题解析
18. 解方程：(x＋3)²＝2(x＋3)；

查看试题解析
19. 用配方法求证：代数式 $3 x^{2} - 6 x + 7$ 的值恒为正数．

查看试题解析
20. 已知 $▱ A B C D$ 的两边 $A B 、 B C$ 的长是关于 $x$ 的方程 $x^{2} - (m + 3) x + 2 m + 2 = 0$ 的两个实数根，当 $m$ 为何值时，四边形 $A B C D$ 是菱形？写出解题过程．

查看试题解析
21. 如图，正方形ABCD中，对角线AC与BD相交于O点，作 $O E ⊥ O F$ 分别交AB、BC于点E、F ，若AE＝4，CF＝3，则EF的长是多少？

查看试题解析
22. 已知方程 $x^{2} + x - 6 = 0$ 的负数根也是方程 $x^{2} - 2 x + a = 0$ 的一个根，求 $a$ 的值．

查看试题解析
23. 已知关于x的方程mx²﹣（m+2）x+2=0（m≠0）．

(1)、求证：方程总有两个实数根；

(2)、若方程的两个实数根都是整数，求正整数m的值．

查看试题解析
24. 为了调动同学们学习数学的积极性，班内组织开展了“数学小先生”讲题比赛，老师将四道备讲题的题号1，2，3，4，分别写在完全相同的4张卡片的正面，将卡片背面朝上洗匀．

(1)、随机抽取一张卡片，卡片上的数字是“4”的概率是；

(2)、小明随机抽取两张卡片，用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率．

查看试题解析

25. 小敏与小霞两位同学解方程

3 (x - 3) = {(x - 3)}^{2}

的过程如下框：

小敏：

两边同除以 $(x - 3)$ ，得

$3 = x - 3$ ，

则 $x = 6$ ．

小霞：

移项，得 $3 (x - 3) - {(x - 3)}^{2} = 0$ ，

提取公因式，得 $(x - 3) (3 - x - 3) = 0$ ．

则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ ，

解得 $x_{1} = 3$ ， $x_{2} = 0$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

26. 如图，在四边形ABCD中，AB $∥$ CD，AC平分∠DAB，AB＝2CD，E为AB中点，连接CE.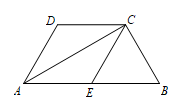

(1)、求证：四边形AECD为菱形；

(2)、若∠D＝120°，DC＝2，求△ABC的面积.

查看试题解析
27. 2020年秋冬以来，由于全国大葱种植面积的减少与产量的减产，10月份到12月份，大葱的批发价格持续走高。10月份大葱的批发价格为5元/公斤，12月份大葱的批发价格涨到7.2元/公斤．

(1)、求10月份到12月份大葱批发价格的月平均增长率；

(2)、进入12月份以来，某农贸市场按照7.2元/公斤的批发价购进大葱进行销售，销售价格为10元/公斤，每天能销售大葱500公斤，为了扩大销售，增加盈利，最大限度让利于顾客，该农贸市场决定对大葱进行降价销售，根据市场调查发现，大葱的销售单价每降低0.1元，每天的销售量将增加40公斤，求当大葱的销售价格降低多少元时，该农贸市场每天销售大葱的利润为1640元？

查看试题解析
28. 如图，平行四边形 $A B C D$ 中， $A D = 9 c m$ ， $C D = 3 \sqrt{2} c m$ ， $∠ B = 45 °$ ，点 $M$ ， $N$ 分别以 $A$ ， $C$ 为起点， $1 c m / 秒$ 的速度沿 $A D$ ， $C B$ 边运动，设点 $M$ ， $N$ 运动的时间为 $t$ 秒 $(0 \leq t \leq 6)$ ．

(1)、求 $B C$ 边上高 $A E$ 的长度；

(2)、连接 $A N$ ， $C M$ ，当 $t$ 为何值时，四边形 $A M C N$ 为菱形；

(3)、作 $M P ⊥ B C$ 于 $P$ ， $N Q ⊥ A D$ 于 $Q$ ，当 $t$ 为何值时，四边形 $M P N Q$ 为正方形．

查看试题解析

实验次数	100	500	1000	2000	4000
频率	0.37	0.32	0.345	0.339	0.333