山东省烟台市芝罘区2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题（每题3分，满分36分）

1. 下列因式分解正确的是（）

A、 $a x + y = a (x + y)$ B、 $x^{2} + x - 2 = x (x + 1) - 2$ C、 $2 x^{2} - x = x (2 x - 1)$ D、 $x^{2} - 16 = {(x - 4)}^{2}$

查看试题解析
2. 下列等式成立的是（）

A、 $\frac{1}{a} - \frac{1}{b} = \frac{1}{a - b}$ B、 $\frac{- x + y}{x + y} = - 1$ C、 $\frac{x - y}{y - x} = - 1$ D、 $\frac{x + 1}{y + 1} = \frac{x}{y}$

查看试题解析
3. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值为（）

A、-3 B、3 C、-3或3 D、0或3

查看试题解析
4. 分式方程 $\frac{x}{x - 1} - 3 = \frac{k}{1 - x}$ 去分母后，正确的是（）

A、 $x - 3 = k$ B、 $x - 3 = - k$ C、 $x - 3 (x - 1) = k$ D、 $x - 3 (x - 1) = - k$

查看试题解析
5. 下列多项式能用完全平方公式因式分解的是（）

A、 $a^{2} - 4 a b + 4 b^{2}$ B、 $a^{2} - 4 a b - 4 b^{2}$ C、 $- a^{2} + 4 a b + 4 b^{2}$ D、 $a^{2} - 2 a b + 4 b^{2}$

查看试题解析
6. 某滑雪俱乐部12名会员被分成甲、乙两组，他们的身高情况如图所示，甲组身高的平均数为 $\bar{x_{甲}} = 176 c m$ ，则下列结论正确的是（）

A、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ B、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$ C、 $\bar{x_{甲}} < \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ D、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$

查看试题解析
7. 计算 ${(- 2)}^{2023} + 2^{2022}$ 的结果是（）

A、-2 B、 $- 2^{2022}$ C、 $2^{2022}$ D、 $- 2^{2023}$

查看试题解析
8. 世界文化遗产“三孔”景区已经完成5G基站布设，“孔夫子家”自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍，在峰值速率下传输500兆数据，5G网络比4G网络快45秒，求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x兆数据，依题意，可列方程是（）

A、 $\frac{500}{x} - \frac{5000}{x} = 45$ B、 $\frac{5000}{x} - \frac{500}{x} = 45$ C、 $\frac{500}{10 x} - \frac{500}{x} = 45$ D、 $\frac{500}{x} - \frac{500}{10 x} = 45$

查看试题解析
9. 为庆祝中国共产党成立102周年，某学校开展“学党史，跟党走”师生阅读活动，老师每周对各小组阅读情况进行综合评分.下表是其中一周的评分结果：
组别
一
二
三
四
五
六
七
分值
90
96
90
89
91
85
90
则“分值”这组数据的中位数和众数分别是（）

A、89，90 B、90，95 C、88，95 D、90，90

查看试题解析
10. 已知 $x^{2} = 2 y + 7$ ， $y^{2} = 2 x + 7$ ，且 $x \neq y$ ，则xy的值为（）

A、7 B、3 C、-3 D、-7

查看试题解析
11. 若关于x的分式方程 $\frac{6}{x - 1} = \frac{x + 3}{x (x - 1)} - \frac{k}{x}$ 无解，则k的取值是（）

A、 $k = - 3$ B、 $k = - 3$ 或 $k = - 5$ C、 $k = 1$ D、 $k = 1$ 或 $k = - 5$

查看试题解析
12. 对于两个不相等的实数a ， b ，我们规定符号 $m a x | a ， b |$ 表示a ， b中较大的值，如 $m a x | 2 ， 4 | = 4$ .按照这个规定，方程 $m a x | \frac{2}{x} ， - \frac{2}{x} | = \frac{3}{x - 1} (x > 0)$ 的解为（）

A、-1或-2 B、-2 C、无解 D、-1

查看试题解析

二、填空题（每题3分，满分24分）

13. 若分式 $\frac{x}{x - 1}$ 有意义，则x的值为.

查看试题解析
14. 计算 $1 \div (- a) \cdot \frac{1}{a}$ 的结果是.

查看试题解析
15. 体育课某次体能测试，5名学生的平均分是92分，其中两人的平均分是95分，则其余3名学生的平均分是.

查看试题解析
16. 若 $(x - 2)$ 是多项式 $x^{3} + 3 x^{2} - 8 x + k$ 的一个因式，则k的值是.

查看试题解析
17. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，评价成绩80分以上（含80分）为“优秀”.下面表中是小王同学的成绩记录：
项目
完成作业
单元测试
期末考试
成绩
65
75

若完成作业、单元检测、期末考试三项成绩按1：3：6的权重来确定期末评价成绩，小王的期末评价为优秀，那么他的期末考试最低成绩是.

查看试题解析
18. 已知m、n互为相反数，且满足 ${(m + 4)}^{2} - {(n + 4)}^{2} = 16$ ，则 $m^{2} + n^{2} - \frac{m}{n}$ 的值是.

查看试题解析
19. 现在生活人们已经离不开密码，如取款、上网等都需要密码，有一种用“因式分解”法产生的密码，方便记忆。原理是：如对于多项式 $x^{4} - y^{4}$ ，因式分解的结果是 $(x - y) (x + y) (x^{2} + y^{2})$ ，若取 $x = 9$ ， $y = 9$ 时则各个因式的值是： $x - y = 0$ ， $x + y = 18$ ， $x^{2} + y^{2} = 162$ ，把这些值从小到大排列得到018162，于是就可以把“018162”作为一个六位数的密码.对于多项式 $4 x^{3} - x y^{2}$ ，取 $x = 21$ ， $y = 19$ 时，请你写出一个用上述方法产生的密码.

查看试题解析
20. 观察下列各式： $\frac{1}{1 \times 3} = \frac{1}{2} (1 - \frac{1}{3})$ ， $\frac{1}{3 \times 5} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5})$ ， $\frac{1}{5 \times 7} = \frac{1}{2} (\frac{1}{5} - \frac{1}{7})$ ， .....，根据观察，计算； $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + ⋯ + \frac{1}{4 n^{2} - 1}$ 的结果是（n为正整数）.

查看试题解析

三、解答题（共7道题，满分60分）

21. 因式分解：

(1)、 $2 x^{2} y - 8 x y + 8 y$

(2)、 ${(m^{2} - 5)}^{2} + 2 (m^{2} - 5) + 1$

查看试题解析
22. 解分式方程： $\frac{9 x - 7}{3 x - 2} - 1 = \frac{4 x - 5}{2 - 3 x}$

查看试题解析
23. 已知关于x的分式方程 $\frac{2 x - m}{x - 1} - \frac{3}{1 - x} = 1$ 的解是正数，求m的取值范围.

查看试题解析
24. 我市某中学举办“网络安全知识竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示：

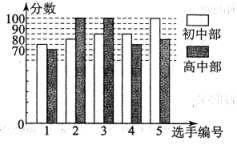
平均数
中位数
众数
方差
初中部
a
85
b
$s^{2}$
高中部
85
c
100
160

(1)、根据图示求出a= ， b= ， c=；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩好？

(3)、计算初中代表队决赛成绩的方差 $s^{2}$ ，并判断哪一个代表队选手成绩较为稳定.

查看试题解析
25. 已知： $a > 0$ ， $b > 0$ ， $\frac{a}{b} + \frac{b}{a} + 2 = a b$ ，且 $a \neq b$ .

(1)、求证： $a + b = a b$ ；

(2)、求 $\frac{a^{2}}{2 a - 2 b} - \frac{a^{2}}{2 a + 2 b} - \frac{a b^{2} + a^{2} b}{2 a^{2} - 2 b^{2}}$ 的值.

查看试题解析
26. 节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶，某品牌油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，则费用为80元；若完全用电做动力行驶，则费用为30元，已知汽车行驶中每千米用油费用比用电费用多0.5元.

(1)、求汽车行驶中每千米用电费用是多少元？甲、乙两地的距离是多少千米？

(2)、若汽车从甲地到乙地采用油电混合动力行驶，要使行驶总费用不超过60元，求至少需要用电行驶多少千米？

查看试题解析
27. 观察下列分解因式的过程： $x^{2} + 2 x y - 3 y^{2}$
解：原式 $= x^{2} + 2 x y + y^{2} - y^{2} - 3 y^{2}$
$= (x^{2} + 2 x y + y^{2}) - 4 y^{2}$
$= {(x + y)}^{2} - {(2 y)}^{2}$
$= (x + y + 2 y) (x + y - 2 y)$
$= (x + 3 y) (x - y)$
像这种通过增减项把多项式转化成适当的完全平方形式的方法，在代数计算与推理中往往能起到巧妙解题的效果.

(1)、请你运用上述方法分解因式： $x^{2} + 4 x y - 5 y^{2}$ ；

(2)、若 $M = 2 (3 x^{2} + 3 x + 1)$ ， $N = 4 x^{2} + 2 x - 3$ ，比较M、N的大小，并说明理由；

(3)、已知 $R t △ A B C$ 中， $∠ C = 90 °$ ，三边长a ， b ， c满足 $c^{2} + 25 = 8 a + 6 b$ ，求 $△ A B C$ 的周长.

查看试题解析

	平均数	中位数	众数	方差
初中部	a	85	b	$s^{2}$
高中部	85	c	100	160

组别	一	二	三	四	五	六	七
分值	90	96	90	89	91	85	90

项目	完成作业	单元测试	期末考试
成绩	65	75