吉林省名校调研（省命题三十七）2023-2024学年八年级上学期期中测试数学试卷
试卷更新日期：2023-11-24 类型：期中考试
一、选择题（每小题2分，共12分）
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 若一个三角形的三边长分别为2、6、a，则a的值可以是（ ）A、8 B、7 C、4 D、33. 如图，∠ACD=120°，∠B=20°，则∠A的度数是（ ）
A、120° B、90° C、100° D、30°4. 如图，点P是AB上任意一点，∠ABC=∠ABD，从下列条件中补充一个条件，不一定能推出△APC≌△APD的是（ ）
A、BC=BD B、∠ACB=∠ADB C、AC=AD D、∠CAB=∠DAB5. 三个等边三角形的摆放位置如图所示，若∠1+∠2=100°，则∠3的度数为（ ）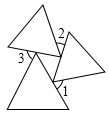
A、 B、 C、 D、6. 如图所示的五边形花环是用五个全等的等腰三角形拼成的，则∠BAC的度数为（ ）
A、28° B、36° C、45° D、72°二、填空题（每小题3分，共24分）
-
7. 如图，生活中会把花架做成三角形的支架，这是利用了三角形的
8. 在平面直角坐标系中．点P（-1，-5）关于y轴对称的点的坐标是9. 如图，点D与点D'关于AE对称，若∠CED'=60°．则∠AED =度．
10. 如图，已知OA=5cm，P是射线ON上的一动点，∠AON=60°，则当OP=cm时，△AOP是等边三角形．
11. 如图，AD是△ABC的中线，E是AB的中点，连接DE，若△ABC的面积为24，则△BDE的面积为
12. 如图，是的平分线，于点D ， 于点C ， 则关于直线对称的三角形共有对．
13. 如图，点E、A、C在同一条直线上，AB∥CD，AB=CE，AC=CD，若∠D=40°，∠ECD=115°，则∠B=度．
14. 如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，若∠A =∠ABE，AC = 10，BC = 6，则BD的长为
三、解答题（每小题5分，共20分）
-
15. 已知一个多边形的内角和的等于它的外角和，求这个多边形的边数．16. 如图，在△ABC中，过点A作AE⊥BC，垂足为E，延长EA至点D，使AD=AC．在边AC上取一点F．连接DF．若∠DAF=110°，∠BAE=40°，∠D=∠C，求证：AF=AB．
17. 如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上．
(1)、图中点D的对应点是点 ， AE的对应边是；(2)、若∠DAE=108°，∠EAF=39°，求∠DAC的度数．18. 如图，AB=CD，AE⊥BC于点E，DF⊥BC于点F，且AE=DF．判断BF和CE的数量关系．并说明理由．
四、解答题（每小题7分，共28分）
-
19. 如图，A、B两点位于高墙外，不能直接测量出A、B间的距离．学习了三角形全等知识后，小明给出了如下的方案：先在地面上取一点可以直接到达A点和B点的点O，连接AO并延长到C，使OC=OA；连接BO并延长到D，使OD=OB，连接CD并测量出CD的长度，CD的长度就是A、B间的距离，请根据以上的信息，说明AB=CD．
20. 如图，在四边形ABCD中，∠B=50°，∠C=110°，∠D=90°，AE⊥BC，AF是∠BAD的平分线，与边BC交于点F．
(1)、求∠DAE的度数；(2)、∠EAF=度．21. 如图，△ABC的边AC与△CDE的边CE在一条直线上，且点C为AE的中点，AB=CD，BC=DE．
(1)、求证：△ABC≌△CDE；(2)、判断BC与DE的位置关系，并说明理由．22. 图①、图②均是6×6的正方形网格，每个小正方形的顶点叫做格点，每个小正方形的边长都是1，点A、B、E、F均在格点上．在图①、图②中，只用无刻度的直尺，在给定的网格中按要求画图，使所画图形的顶点均在格点上，不要求写画法．
(1)、在图①中，以线段AB为底画一个等腰三角形ABC，且顶角为锐角；(2)、在图②中，以线段EF为对角线画一个轴对称四边形EMFN，使其面积为4．五、解答题（每小题8分，共16分）
-
23. 如图，直线AB∥CD，∠ACD的平分线CE交AB于点F，c LAFE的平分线交CA的延长线于点G．
(1)、求证：△ACF是等腰三角形；(2)、若∠FCD=30°，求∠G的大小．24. 如图，在△ABC中，AB=AC，D是BC的中点，EF垂直平分AC，交AC于点E，交AB于点F，M是直线EF．上的动点．
(1)、当MD⊥BC时．①若ME=1，则点M到AB的距离为 ▲
②若∠CMD=30°，CD=3，求△BCM的周长；
(2)、若BC=8，且△ABC的面积为40，则△CDM的周长的最小值为六、解答题（每小题10分，共20分）
-
25. 如图①，在△ABC中，∠ACB=90°，AC=BC，点P是线段AB上的一点，过点A作AE⊥CP，交CP的延长线于点E，过点B作BF⊥CP于点F．
(1)、若BF=8，AE=3，则EF=(2)、在图①中，线段AE、BF、EF有怎样的数量关系？请说明理由；(3)、如图②，在△ABC中，∠ACB=90°，AC=BC，点P是△ABC内部的一点，且BP⊥CP，连接AP，若CP=5，求△ACP的面积．26. 在边长为9cm的等边三角形ABC中，点Q是BC边上的一点，动点P以1cm/s的速度从点A沿AB向点B运动，设运动时间为t（s）．
(1)、如图①，若BQ=6，PQ∥AC，求t的值；(2)、如图②，若点P从点A向点B运动的同时，点Q以2cm/s的速度从点B沿BC-CA向点A运动，求t为何值时，OAPQ是等边三角形；(3)、如图③，将边长为9cm的等边三角形ABC变换为以AB、AC为腰、BC为底的等腰三角形，且AB=AC=10cm，BC=8cm，点P运动到AB的中点处停止．点P停止运动后，点M以1cm/s的速度从点B沿BC向点C运动，同时点N以acm/s的速度从点C沿CA向点A运动，当△BPM与△CNM全等时，直接写出a的值．