吉林省四平市铁西区2023-2024学年八年级上学期期中考试数学试题
试卷更新日期:2023-11-24 类型:期中考试
一、单项选择题(每小题2分,共12分)
-
1. 下列品牌的标识中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用直角三角板作△ABC的高,下列作法正确的是( )A、
2. 用直角三角板作△ABC的高,下列作法正确的是( )A、 B、
B、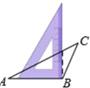 C、
C、 D、
D、 3. 空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
3. 空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( ) A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 已知图中的两个三角形全等,则∠1等于( )
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短4. 已知图中的两个三角形全等,则∠1等于( )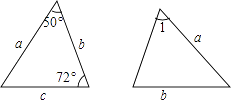 A、50° B、58° C、60° D、72°5. 小明用长度分别为5,a,9的三根木棒首尾相接组成一个三角形,则a可能是( ).A、 B、 C、 D、6. 如图,正方形纸片ABCD:①先对折使AB与CD重合,得到折痕EF;②折叠纸片,使得点A落在EF的点H上,沿BH和CH剪下△BCH.则判定△BCH为等边三角形的依据是( )
A、50° B、58° C、60° D、72°5. 小明用长度分别为5,a,9的三根木棒首尾相接组成一个三角形,则a可能是( ).A、 B、 C、 D、6. 如图,正方形纸片ABCD:①先对折使AB与CD重合,得到折痕EF;②折叠纸片,使得点A落在EF的点H上,沿BH和CH剪下△BCH.则判定△BCH为等边三角形的依据是( ) A、三个角都相等的三角形是等边三角形 B、有两个角是60°的三角形是等边三角形 C、三边都相等的三角形是等边三角形 D、有一个角是60°的等腰三角形是等边三角形
A、三个角都相等的三角形是等边三角形 B、有两个角是60°的三角形是等边三角形 C、三边都相等的三角形是等边三角形 D、有一个角是60°的等腰三角形是等边三角形二、填空题(每小题3分,共24分)
-
7. 点M(1, 2)关于x轴对称点的坐标为8. 若一个多边形的每一个外角都等于40°,则这个多边形是边形.9. 如图,点A、E、B、F在同一条直线上,AC∥DF,AC=DF,要使△ABC≌△FED,则可以补充一个条件:
 10. 如图是由一副三角板拼凑得到的,图中的∠ABC的度数为度.
10. 如图是由一副三角板拼凑得到的,图中的∠ABC的度数为度. 11. 如图,在△ABC中,AB的垂直平分线DE与边AB, AC分别交于点D,E.已知△ABC与△BCE的周长分别为22cm和14cm,则BD的长为cm.
11. 如图,在△ABC中,AB的垂直平分线DE与边AB, AC分别交于点D,E.已知△ABC与△BCE的周长分别为22cm和14cm,则BD的长为cm.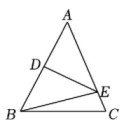 12. 如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是度.
12. 如图,在△ABC中,∠B=30°,∠C=50°,通过观察尺规作图的痕迹,∠DEA的度数是度. 13. 如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,点E为AB的中点,若AB=12,CD=3,则△DBE的面积为
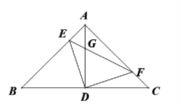
13. 如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,点E为AB的中点,若AB=12,CD=3,则△DBE的面积为 14. 如图,在△ABC中,∠BAC= =90°,AB=AC, D是BC的中点,点E、F分别在边AB、AC上,且∠EDF=90°.下列结论正确的是 (填所有正确答案的序号).
14. 如图,在△ABC中,∠BAC= =90°,AB=AC, D是BC的中点,点E、F分别在边AB、AC上,且∠EDF=90°.下列结论正确的是 (填所有正确答案的序号).①△ADE≌△CDF;②AC=BE+CF;③EF=AD;
三、解答题(每小题5分,共20分)
-
15. 如图,在△ABC中,∠B=30°,∠C=50°,∠BAC的平分线AD交BC于点D.求∠DAC与∠ADB的度数.
 16. 如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,求证:BC=CD.
16. 如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,求证:BC=CD. 17. 如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠A=∠D.
17. 如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠A=∠D.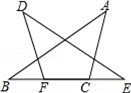 18. 下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.
18. 下列正方形网格图中,部分方格涂上了阴影,请按照不同要求作图.如图①,将某一个方格涂上阴影,使整个图形有两条对称轴.
如图②,将某一个方格涂上阴影,使整个图形有四条对称轴.

四、解答题(每题7分,共28分)
-
19. 如图所示,根据图中的对话回答问题.
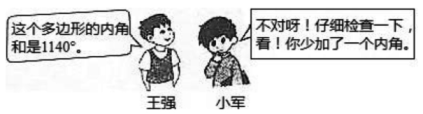 (1)、王强是在求几边形的内角和?(2)、少加的那个内角为多少度?20. 如图,点D在BC边上,△ABC≌△ADE,∠B=70°,请求出∠EAC的度数.
(1)、王强是在求几边形的内角和?(2)、少加的那个内角为多少度?20. 如图,点D在BC边上,△ABC≌△ADE,∠B=70°,请求出∠EAC的度数. 21. 如图,在平面直角坐标系中,A(-1,2)、B(-4,0)、C(-3,-2).
21. 如图,在平面直角坐标系中,A(-1,2)、B(-4,0)、C(-3,-2). (1)、在图中作出△ABC关于y轴的对称图形△A'B'C,并写出点B'的坐标;(2)、请直接写出△ABC的面积;(3)、若点M(m-1,3)与点N(-2,n+1)关于x轴对称,请直接写出m、n的值.22. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,请求出∠CDE的度数.
(1)、在图中作出△ABC关于y轴的对称图形△A'B'C,并写出点B'的坐标;(2)、请直接写出△ABC的面积;(3)、若点M(m-1,3)与点N(-2,n+1)关于x轴对称,请直接写出m、n的值.22. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,请求出∠CDE的度数.
五、解答题(每题8分,共16分)
-
23. 如图,CB=CD,∠D+∠ABC=180°,CE⊥AD于E,CF⊥AB交AB的延长线于点F.
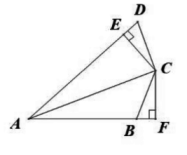 (1)、求证:AC平分∠DAB;(2)、若AE=8,DE=2,求AB的长.24. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,CD平分∠ACB,交边AB于点D,点E是边AB的中点.点P为边CB上的一个动点.
(1)、求证:AC平分∠DAB;(2)、若AE=8,DE=2,求AB的长.24. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=3,CD平分∠ACB,交边AB于点D,点E是边AB的中点.点P为边CB上的一个动点.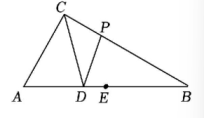 (1)、AE= , ∠ACD=度;(2)、当四边形ACPD为轴对称图形时,求CP的长;(3)、若△CPD是等腰三角形,请直接写出∠CDP的度数;
(1)、AE= , ∠ACD=度;(2)、当四边形ACPD为轴对称图形时,求CP的长;(3)、若△CPD是等腰三角形,请直接写出∠CDP的度数;六、解答题(每题10分,共20分)
-
25. 如图,已知A(0,-6),B (6,0),D为第一象限内一点,AD交x轴于点C,DE⊥x轴于点E,BF⊥AD垂足为点H,交OD于点F,线段AC上有一动点G,连接OG.
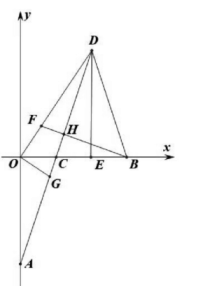 (1)、若AC=CD=DB,
(1)、若AC=CD=DB,①请说明△ACO≌△DCE;
②请求出点C的坐标;
(2)、若∠DOG=90°,试探究AD,DG,BF之间的数量关系,说明理由;26. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点O是线段AD上一点,点P是BA延长线上一点,且OP=OC. (1)、请直接写出线段OB和OP之间的数量关系:(2)、请说明:∠APO+∠DCO=30° ;(3)、请说明:△POC是等边三角形;(4)、请直接写出线段AB、OA、AP之间的数量关系.
(1)、请直接写出线段OB和OP之间的数量关系:(2)、请说明:∠APO+∠DCO=30° ;(3)、请说明:△POC是等边三角形;(4)、请直接写出线段AB、OA、AP之间的数量关系.