吉林省名校调研（省命题十）2023-2024学年九年级上学期期中考试数学试卷

试卷更新日期：2023-11-24 类型：期中考试

进入 出卷网 下载

一、选择题（每小题2分，共12分）

  • 1. 抛物线y=-9（x-7）2的顶点坐标是（    ）
    A、（9，0） B、（-9，7） C、（9，-7） D、（7，0）

    查看试题解析

  • 2. 如图所示的交通标志中，是中心对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 若x=a．是关于x的一元二次方程x2+3x-5= 0的一个根，则-a2-3a的值为（发 ）
    A、0 B、3 C、-5 D、5

    查看试题解析

  • 4. 二次函数y=ax2+bx+c的部分图象如图所示，对称轴为x=-1，图象与x轴相交于点（1，0），则方程ax2+bx+c= 0的根为（    ）

    A、x1=1，x2=-3 B、x1=-1，x2=3 C、x1=1，x2= −13 D、x1=-1，x2= 13

    查看试题解析

  • 5. 某人患了流感，经过两轮传染后共有36人患了流感，设每一轮传染中平均每人传染了x人，则可列方程（    ）
    A、x+（1+x）=36 B、1+x+x（1+x）=36 C、2（1+x）=36 D、1+x+x2=36

    查看试题解析

  • 6. 为了使居住环境更加美观，某小区建造了一个小型喷泉，水流从地面上的点O喷出，在各个方向上沿形状相同的抛物线落到地面，某方向上抛物线的形状如图所示，落点A到点O的距离为4，水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系式y=ax2+245x ， 则水流喷出的最大高度为（　　）

    A、245m B、5m C、112m D、6m

    查看试题解析

二、填空题（每小题3分，共24分）

  • 7. 如图所示的图案绕中心旋转n°后能与原来的图案完全重合，则n的最小值为

    查看试题解析

  • 8. 若关于x的一元二次方程mx2+2x+m2-1=0的常数项为0，则m=

    查看试题解析

  • 9. 若二次函数y=（2a-6）x2+4的图象开口向下，则a的取值范围是

    查看试题解析

  • 10. 如图，△AOB与△OOD关于点O成中心对称，已知∠BAO=90°，AB=4，AO=3，则AD的长为

    查看试题解析

  • 11. 已知抛物线y=-x2-6x+m与x轴没有交点，则m的取值范围是

    查看试题解析

  • 12. 一个三角形的两边长分别为2和3，第三边的长是方程x2-10x+21=0的根，则该三角形的第三边的长为

    查看试题解析

  • 13. 如图，在△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转，得到△EDC，使点B的对应点D恰好落在AB边上，AC、ED交于点F．若∠BCD=50°，则∠EFC=度．

    查看试题解析

  • 14. 如图①，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A、B（点A在点B的左侧），根据对称性知△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”。如图②，抛物线y=x2的“完美三角形”的斜边AB的长为

    查看试题解析

三、解答题（每小题5分，共20分）

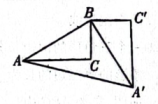
  • 15. 解方程：3x（x-1）=2x-2．

    查看试题解析

  • 16. 已知抛物线y=12（x+h）2+k的顶点坐标为（2，8），求抛物线与y轴的交点坐标．

    查看试题解析

  • 17. 如图，在Rt△ABC中，∠C=90°，∠BAC=30°，BC=2，以点B为旋转中心，把Rt△ABC逆时针旋转90°，得到△A'BC'，连接AA'，求AA'的长，

    查看试题解析

  • 18. 已知二次函数y=-x2+8x-7．
    (1)、直接写出当x为何值时，y随x的增大而增大；
    (2)、直接写出当x为何值时，y<0．

    查看试题解析

四、解答题（每小题7分，共28分）

  • 19. 如图是由边长为1的小正方形构成的4×4的正方形网格，线段AB、EF的端点均在格点上，请按要求画图．

    (1)、在图①中，以AB为边画一个面积是9的四边形，使它的另外两个顶点在格点上，且该四边形是中心对称图形，但不是轴对称图形；
    (2)、在图②中，以EF为对角线画一个四边形，使它的另外两个顶点在格点上，且该四边形既是轴对称图形又是中心对称图形．

    查看试题解析

  • 20. 如图，抛物线y=a（x-2）2-2（a≠0）与x轴交于原点O与点A，点B为顶点．

    (1)、求抛物线的解析式；
    (2)、已知Q（-1，-2） ，将该抛物线向下平移k个单位长度，若平移后的抛物线与线段BQ只有一个公共点，直接写出k的取值范围．

    查看试题解析

  • 21. 如图，在平面直角坐标系中，△ABC的顶点C的坐标为（-4，1）．

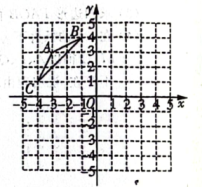    (1)、画出△A1B1C1 ， 使△A1B1C1与△ABC关于原点O对称；并写出点C的对应点C1的坐标；
    (2)、以O为旋转中心，将△ABC逆时针旋转90°得到△A2B2C2 ， 画出△A2B2C2并写出点C的对应点C2的坐标．

    查看试题解析

  • 22. 如图，用40m的篱笆围成一个一边靠墙的矩形场地，墙长15m，垂直于墙的边长为xm，围成的矩形场地的面积为ym2 ．

    (1)、求y与x的函数关系式，并写出自变量x的取值范围；
    (2)、求这个矩形场地面积的最大值．

    查看试题解析

五、解答题（每小题8分，共16分） ，

  • 23. 如图，已知抛物线y=-x2+6x，点P是第一象限内抛物线上的一个动点，作PA⊥x轴于点A，点B是第一象限内抛物线上的另一个点（点B在AP的右侧），且BP=BA，作BC⊥x轴于点C．

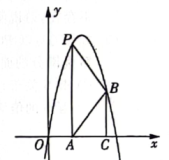    (1)、若点P的横坐标为2，求点B的坐标；
    (2)、若点B关于AP的对称点恰好落在y轴上时，求AC的长．

    查看试题解析

  • 24. 阅读下面材料，并解决问题：

    (1)、如图①，在等边△ABC内有一点P ，若点P到顶点A、B、C的距离分别为3、4、5，求∠APB的度数；为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP'处，此时△ACP'≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB的度数，请你按照这个思路写出求解过程；
    (2)、能力提升

    如图②，在Rt△ABC中，∠ACB=90°，AC=1，∠ABC=30°，点O为Rt△ABC内一点，连接AO、BO、CO，且∠AOC=∠COB=∠BOA=120°，直接写出OA+OB+OC的值．

    查看试题解析

六、解答题（每小题10分，共20分}

  • 25. 如图①，在Rt△ABC中，∠C=90°，AC=BC=6cm，动点P从点C出发，以1cm/s的速度沿CA匀速运动，同时动点Q从点A出发，以2cm/s的速度沿AB匀速运动，当点P到达点A时，点P、Q同时停止运动，设运动时间为t（s）．

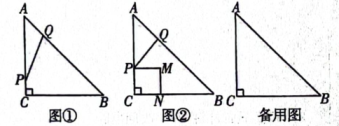    (1)、当t=3时，线段PQ的长为cm；
    (2)、是否存在某一时刻t，使点B在线段PQ的垂直平分线上？若存在，请求出t的值；若不存在，请说明理由；
    (3)、如图②，以PC为边，向PC右侧作正方形CPMN，设正方形CPMN与Rt△ABC重叠部分的面积为S．

    ①求S关于t的函数关系式；

    ②当S的值为14时，直接写出t的值．

    查看试题解析

  • 26. 如图，在平面直角坐标系中，直线y=x+b与x轴交于点A（4，0），与y轴交于点B，过，A、B两点的抛物线交x轴于另一点C，且OA=2OC，点F是直线AB下方抛物线上的一个动点，连接FA、FB．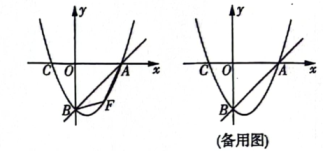

    (1)、求抛物线的解析式；
    (2)、当点F与抛物线的顶点重合时，△ABF的面积为 ；
    (3)、求四边形FAOB面积的最大值及此时点F的坐标；
    (4)、在（3）的条件下，点Q为平面内y轴右侧的一点，是否存在点Q及平面内另一点M，使得以A、F、Q、M为顶点的四边形是正方形？若存在，直接写出点Q的坐标；若不存在，说明理由．

    查看试题解析