吉林省名校调研（省命题十）2023-2024学年八年级上学期期中考试数学试卷

试卷更新日期：2023-11-24 类型：期中考试

进入 出卷网 下载

一、选择题（每小题2分，共12分）

  • 1. 下面几幅图片是校园中运动场上代表体育项目的图标，其中可以看作是轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如图，△ABC的边AC上的高是（ ）

    A、线段AE B、线段BA C、线段BD D、线段BC

    查看试题解析

  • 3. 在下列长度的四组线段中，能组成三角形的是（    ）
    A、2、3、6 B、3、5、9 C、3、4、5 D、2、3、5

    查看试题解析

  • 4. 如图；直线a∥b，等边三角形ABC的顶点C在直线b上，若∠1=40°，则∠2等于（    ）

    A、80° B、70° C、60° D、50°

    查看试题解析

  • 5. 如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（　　）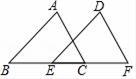

    A、∠A＝∠D B、BC＝EF C、AC＝DF D、∠ACB＝∠F

    查看试题解析

  • 6. 如图，在△ABC中，AB=AC，∠B=30°，D为BC上一点，若CD=AD=4，则BC的长为（    ）

    A、10 B、12 C、14 D、16

    查看试题解析

二、填空题（每小题3分，共24分）

  • 7. 匠人制作马扎时，支撑架都设计成如图形状，这种方法是利用了三角形的 .

    查看试题解析

  • 8. 如图，△ABO≌△DCO，点B、D、A、C在同一直线上，若AD=1，BC=9，则BD=

    查看试题解析

  • 9. 若等腰三角形的一边长为3，另一边长为7，则这个三角形的周长为

    查看试题解析

  • 10. 如图，在△ABC中，AB=15，BC=9，BD是AC边上的中线，若△ABD的周长为35，则△BCD的周长是

    查看试题解析

  • 11. 如图，在△ABC中，AB=5，AC=7，MN为BC边的垂直平分线，若点D在直线MN上，连接AD、BD，则△ABD周长的最小值为 ．

    查看试题解析

  • 12. 如图，为了测量A、B两点之间的距离，在地面上找到一点C，连接BC、AC，使∠ACB=90°，然后在BC的延长线上确定点D，使CD=BC，那么只要测量出AD的长度就得到A、B两点之间的距离，其中△ABC≌△ADC的依据是

    查看试题解析

  • 13. 如图，AB是线段CD的垂直平分线，E、F分别是AB上的两点，若∠CEB=30°，∠CDF=40°，则∠ECF的度数为

    查看试题解析

  • 14. 边长相等的正五边形与正六边形按如图所示拼接在一起，则∠ABO的度数为

    查看试题解析

三、解答题（每小题5分，共20分）

  • 15. 一个多边形的内角和等于它的外角和的6倍，求该多边形的边数．

    查看试题解析

  • 16. 如图，在△ABC中，CB⊥AB、∠BAC=45°，F是AB延长线上一点，点E在BC上，且AE=CF．求证：Rt△ABE≌Rt△CBF．

    查看试题解析

  • 17. 如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，EG是线段BD的垂直平分线，连接DE交AC于点F．求证：点E在线段AF的垂直平分线上，

    查看试题解析

  • 18. 如图，AB=CD，BF=DE，E、F是AC上的两点，且：AE=CF．请你判断BF与DE的位置关系，并说明理由．

    查看试题解析

四、解答题（每小题7分；共28分）

  • 19. 如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．

    (1)、若∠B=35°，∠E=25°，求∠CAE的度数；
    (2)、求证：∠BAC=∠B+2∠E．

    查看试题解析

  • 20. 如图，△ABC的三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．

    ⑴在图中作出△ABC关于y轴对称的△A1B1C1 ， 并写出点A1、B1、C1的坐标（点A、B、C的对应点分别是点A1、B1、C1）；

    ⑵在x轴上找一点P，使得PA + PB的距离最短，在图中作出点P的位置．

    查看试题解析

  • 21. 如图，在△ABC中，BD平分∠ABC，CD平分∠ACB，DE⊥AB于点E．

    (1)、若∠ABC=50°，∠ACB=80°，求∠BDC的度数： 
    (2)、若DE=4，BC=12，求△BCD的面积．

    查看试题解析

  • 22. 如图，在△ABC中，D为AC边上一点，DE⊥AB于点E，ED的延长线交BC的延长线于点F，且CD = CF．

    (1)、求证：△ABC是等腰三角形
    (2)、当∠F=    ▲     度时，△ABC是等边三角形？并证明你的结论．

    查看试题解析

五、解答题（每小题8分，共16分）

  • 23. 如图，在△ABC 和△DBC 中，∠ACB＝∠DBC＝90°，点 E 是 BC 的中点，DE⊥AB 于点F，且 AB＝DE．

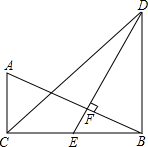    (1)、求证：△ACB≌△EBD；
    (2)、若 DB＝12，求 AC 的长．

    查看试题解析

  • 24. 在四边形ABCD中，∠BAD的平分线与边BC交于点E，∠ADC的平分线交直线AE于点O．

    (1)、若点O在四边形ABCD的内部．

    ①如图①，若AD∥BC，∠B=40°，∠C=70° ，则∠DOE=    ▲     °；

    ②如图②，试判断∠B、∠C、∠DOE之间的数量关系并证明；

    (2)、如图③，若点O在四边形ABCD的外部，请直接写出∠B、∠C、∠DOE之间的数量关系．

    查看试题解析

六、解答题（每小题10分，共20分）

  • 25. 如图，AD为'△ABC的中线，分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF，且AE=AB，AF=AC，连接EF，∠EAF+∠BAC=180°．

    (1)、若∠ABE=63°，∠BAC=45°，求∠FAC的度数；
    (2)、延长AD至点H，使DH=AD，连接BH，求证：∠ABH+∠BAC=180°；
    (3)、在（2）的条件下，请直接写出线段EF和线段AD之间的数量关系．

    查看试题解析

  • 26. 如图，等边△ABC的边长为7cm，现有两动点M．N分别从点A、B同时出发，点M沿折线AC-CB向终点B运动，点N沿折线BA-AC-CB向终点B运动，已知点M的速度为1cm/s，点N的速度为2.5cm/s，当有一点到达终点时另一点也随之停止运动，设运动时间为t（秒）．

    (1)、当M、N两点重合时，求出此时t的值；
    (2)、当点M、N均在边BC上运动时，连接AM、AN，能否得到以MN为底边的等腰三角形AMN？若能，请求出此时MN的长；若不能，请说明理由；
    (3)、在点M，N的运动过程中，当以点M、N及△ARC中的某一顶点为顶点构成的三角形是等边三角形时，请直接写出此时t的值．

    查看试题解析