沪科版数学八年级上册第14章全等三角形判定及性质综合题(拓展提升)
试卷更新日期:2023-11-24 类型:同步测试
一、手拉手模型
-
1. 如图,是边长为2的等边三角形,是延长线上一点,以为边作等边三角形 , 连接.
 (1)、求的度数.(2)、求的值.2. 在等腰中, , 点D在上,延长至点E,使 , 连接 .
(1)、求的度数.(2)、求的值.2. 在等腰中, , 点D在上,延长至点E,使 , 连接 . (1)、若 ,
(1)、若 ,①如图1,求证:;
②如图2,将绕点C按顺时针方向旋转一定的角度,使点A,D,E三点在一条直线上,判定的形状,并说明理由.
(2)、若 , 如图3,(1)中①的结论是否成立?若不成立,请给出 , 之间的数量关系;若成立,请给出证明.3. 已知△ABC与ΔADE均为等腰直角三角形,且∠BAC=∠DAE=90°,点D在直线BC上. (1)、如图1,当点D在CB延长线上时,求证:BE⊥CD;(2)、如图2,当D点不在直线BC上时, BE、CD相交于M,
(1)、如图1,当点D在CB延长线上时,求证:BE⊥CD;(2)、如图2,当D点不在直线BC上时, BE、CD相交于M,①直接写出∠CME的度数;
②求证:MA平分∠CME
4. 在ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作ADE,使AE=AD,∠DAE=∠BAC,连接CE. (1)、如图,当点D在BC延长线上移动时,若∠BAC=26°,则∠DCE= .(2)、设∠BAC=α,∠DCE=β.
(1)、如图,当点D在BC延长线上移动时,若∠BAC=26°,则∠DCE= .(2)、设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
5. 在等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接FC. (1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;(3)、如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.6. 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC.过点C作CF⊥DE交DE于点F.
(1)、如图1,求证:∠ABE=∠ACF;(2)、如图2,当∠ABC=60°时,在BE上取点M,使BM=EF,连接AM.求证:△AFM是等边三角形;(3)、如图3,当∠ABC=45°,且AEBC时,求证:BD=2EF.6. 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC.过点C作CF⊥DE交DE于点F.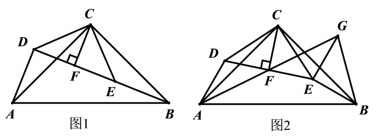 (1)、如图1,当点B、E、D在同一条线上时,
(1)、如图1,当点B、E、D在同一条线上时,①求证:;
②求∠BDA的度数;
(2)、如图2,连接AF并延长至点G,使AF=GF,连接GE、GB,试判断△BEG形状,并说明理由.二、动态几何全等模型
-
7. 如图,与相交于点C, , , , 点P从点A出发,沿方向以的速度运动,点Q从点D出发,沿方向以的速度运动,P、Q两点同时出发,当点P回到点A时,P、Q两点同时停止运动,设点P的运动时间为 .
 (1)、求证: .(2)、写出线段的长(用含t的式子表示).(3)、连接 , 当线段经过点C时,求t的值.8. 如图,已知 中, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由 点向 点运动,设点 运动的时间为 .
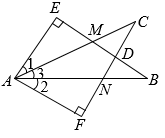
(1)、求证: .(2)、写出线段的长(用含t的式子表示).(3)、连接 , 当线段经过点C时,求t的值.8. 如图,已知 中, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由 点向 点运动,设点 运动的时间为 . (1)、用含 的式子表示 的长为;(2)、若点 的运动速度与点 的运动速度相等,经过 秒后, 与 是否全等?请说明理由;(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?9. 某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知: 中, ;机器人从点 出发,沿着 边按 的方向匀速移动到点 停止;机器人移动速度为每秒 个单位,移动至拐角处调整方向需要 秒(即在 处拐弯时分别用时 秒).设机器人所用时间为 秒时,其所在位置用点 表示(机器人大小不计).
(1)、用含 的式子表示 的长为;(2)、若点 的运动速度与点 的运动速度相等,经过 秒后, 与 是否全等?请说明理由;(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?9. 某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知: 中, ;机器人从点 出发,沿着 边按 的方向匀速移动到点 停止;机器人移动速度为每秒 个单位,移动至拐角处调整方向需要 秒(即在 处拐弯时分别用时 秒).设机器人所用时间为 秒时,其所在位置用点 表示(机器人大小不计). (1)、点 到边 的距离是;(2)、是否存在这样的时刻,使 为等腰三角形?若存在,求出 的值;若不存在,请说明理由.10. 如图(1), , , 垂足分别为A、B , .点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)、点 到边 的距离是;(2)、是否存在这样的时刻,使 为等腰三角形?若存在,求出 的值;若不存在,请说明理由.10. 如图(1), , , 垂足分别为A、B , .点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束). (1)、若点Q的运动速度与点P的运动速度相等,当 时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“ , ”改为“ ”,点Q的运动速度为x cm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.
(1)、若点Q的运动速度与点P的运动速度相等,当 时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)、如图(2),若“ , ”改为“ ”,点Q的运动速度为x cm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.三、一线三等角模型
-
11. 已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E.
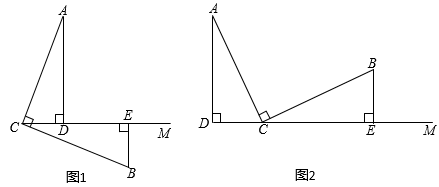 (1)、如图1,①线段CD和BE的数量关系是 ▲ ;②请写出线段AD,BE,DE之间的数量关系并证明.(2)、如图2,上述结论②还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系并证明.12. 如图1,在中, , , 于点 , 于点 .
(1)、如图1,①线段CD和BE的数量关系是 ▲ ;②请写出线段AD,BE,DE之间的数量关系并证明.(2)、如图2,上述结论②还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系并证明.12. 如图1,在中, , , 于点 , 于点 . (1)、求证:;(2)、如图2,若点O为的中点,连接DO,EO,判断的形状,并说明理由.13. 如图所示,回答下列问题
(1)、求证:;(2)、如图2,若点O为的中点,连接DO,EO,判断的形状,并说明理由.13. 如图所示,回答下列问题 (1)、如图1, 在 中, , ,直线 经过点 , 直线 , ⊥直线 ,垂足分别为点 、 .证明: .(2)、如图2,将(1)中的条件改为:在 中, , 、 、 三点都在直线 上,并且有 ,其中 为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图3, 、 是 、 、 三点所在直线 上的两动点( 、 、 三点互不重合),点 为 平分线上的一点,且 和 均为等边三角形,连接 、 ,若 , ,试判断 的形状,并求出 的长.14. 利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
(1)、如图1, 在 中, , ,直线 经过点 , 直线 , ⊥直线 ,垂足分别为点 、 .证明: .(2)、如图2,将(1)中的条件改为:在 中, , 、 、 三点都在直线 上,并且有 ,其中 为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图3, 、 是 、 、 三点所在直线 上的两动点( 、 、 三点互不重合),点 为 平分线上的一点,且 和 均为等边三角形,连接 、 ,若 , ,试判断 的形状,并求出 的长.14. 利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用. (1)、如图①, , , 三点共线, 于点 , 于点 , ,且 .若 ,求 的长.(2)、如图②,在平面直角坐标系中, 为等腰直角三角形,直角顶点 的坐标为 ,点 的坐标为 .求直线 与 轴的交点坐标.(3)、如图③, , 平分 ,若点 坐标为 ,点 坐标为 .则 . (只需写出结果,用含 , 的式子表示)
(1)、如图①, , , 三点共线, 于点 , 于点 , ,且 .若 ,求 的长.(2)、如图②,在平面直角坐标系中, 为等腰直角三角形,直角顶点 的坐标为 ,点 的坐标为 .求直线 与 轴的交点坐标.(3)、如图③, , 平分 ,若点 坐标为 ,点 坐标为 .则 . (只需写出结果,用含 , 的式子表示)四、倍长中线模型
-
15. 如图,在中,为边的中线,E为上一点,连接并延长交于点F,若 , , , 则的长为.
 16.
16. (1)、阅读理解:如图1,在△ABC中,若AB=10,BC=8,求AC边上的中线BD的取值范围.小聪同学是这样思考的:延长BD至E,使DE=BD,连结CE.利用全等将边AB转化到CE,在△BCE中利用三角形三边关系即可求出中线BD的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是;中线BD的取值范围是 .(2)、问题解决:如图2,在△ABC中,点D是AC的中点,点M在AB边上,点N在BC边上,若DM⊥DN,求证:AM+CN>MN.(3)、问题拓展:如图3,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=∠NBC=90°,连接MN,探索BD与MN的关系,并说明理由.17.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:
(1)、阅读理解:如图1,在△ABC中,若AB=10,BC=8,求AC边上的中线BD的取值范围.小聪同学是这样思考的:延长BD至E,使DE=BD,连结CE.利用全等将边AB转化到CE,在△BCE中利用三角形三边关系即可求出中线BD的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是;中线BD的取值范围是 .(2)、问题解决:如图2,在△ABC中,点D是AC的中点,点M在AB边上,点N在BC边上,若DM⊥DN,求证:AM+CN>MN.(3)、问题拓展:如图3,在△ABC中,点D是AC的中点,分别以AB,BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN,其中∠ABM=∠NBC=90°,连接MN,探索BD与MN的关系,并说明理由.17.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:

如图 , 中,若 , , 求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长至点 , 使 , 连接 .
请根据小明的方法思考:
由已知和作图能得到≌ , 依据是 .
A.;;;
由“三角形的三边关系”可求得的取值范围是 .
(2)、【初步运用】如图 , 是的中线,交于 , 交于 , 且若 , , 求线段的长.
(3)、【灵活运用】如图 , 在中, , 为中点, , 交于点 , 交于点 , 连接试猜想线段三者之间的数量关系,并证明你的结论.
五、角平分线模型
-
18. 在 中, 为 的角平分线.


图1 图2
(1)、如图1, , ,点 在边 上, ,请直接写出图中所有与 相等的线段.(2)、如图2, ,如果 ,求证: .19. 如图,在中,平分 , , 垂足为点E . 若的面积为16, , 则的长为( ) A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6六、直角三角形判定HL
-
20. 已知 ≌ , .


 (1)、将 和 按图①方式摆放,使 经过点 ,延长 交线段 于点 .试判断线段 、 、 之间的数量关系,并证明你的结论;(2)、将 和 按图②方式摆放,延 交线段 于点 .请直接写出 、 、 之间的数量关系 .(3)、将 和 按图③方式摆放,延长 交 的延长线于点 .请直接写出线段 、 、 之间的数量关系: .
(1)、将 和 按图①方式摆放,使 经过点 ,延长 交线段 于点 .试判断线段 、 、 之间的数量关系,并证明你的结论;(2)、将 和 按图②方式摆放,延 交线段 于点 .请直接写出 、 、 之间的数量关系 .(3)、将 和 按图③方式摆放,延长 交 的延长线于点 .请直接写出线段 、 、 之间的数量关系: .七、其他综合
-
21. 已知:任意一个三角形的三条角平分线都交于一点.如图,在 中, 、 分别平分 、 ,过点 作直线分别交 、 于点 、 ,若 ,解答下列问题:
 (1)、证明: ;(2)、若 , , , ,求 的长.22. 如图,在中, , 且 , D是的中点,E是延长线上一点,交的延长线于F,的延长线交的延长线于点G,连接 .
(1)、证明: ;(2)、若 , , , ,求 的长.22. 如图,在中, , 且 , D是的中点,E是延长线上一点,交的延长线于F,的延长线交的延长线于点G,连接 .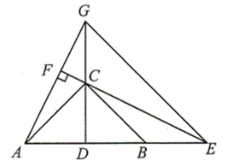 (1)、求证:①;②;(2)、若 , 求的度数.23. 如图,在中,点D是延长线上一点,过点D作于点F,延长交于点E,交的平分线于点N,点M为与的交点, , .
(1)、求证:①;②;(2)、若 , 求的度数.23. 如图,在中,点D是延长线上一点,过点D作于点F,延长交于点E,交的平分线于点N,点M为与的交点, , . (1)、求的度数;(2)、证明:.
(1)、求的度数;(2)、证明:.
-