北京市丰台区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-11-24 类型:期中考试
一、选择题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列四个品牌图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用配方法解一元二次方程x2-8x+3=0,此方程可化为( )A、(x-4)2=13 B、(x+4)2=13 C、(x-4)2=19 D、(x+4)2=193. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( )
2. 用配方法解一元二次方程x2-8x+3=0,此方程可化为( )A、(x-4)2=13 B、(x+4)2=13 C、(x-4)2=19 D、(x+4)2=193. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( ) A、 B、 C、 D、4. 在平面直角坐标系中,将抛物线先向左平移个单位,再向下平移个单位,所得抛物线为( )A、 B、 C、 D、5. 在平面直角坐标系中,二次函数的图象如图所示,关于 , 的符号判断正确的是( )
A、 B、 C、 D、4. 在平面直角坐标系中,将抛物线先向左平移个单位,再向下平移个单位,所得抛物线为( )A、 B、 C、 D、5. 在平面直角坐标系中,二次函数的图象如图所示,关于 , 的符号判断正确的是( )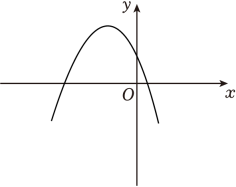 A、 , B、 , C、 , D、 ,6. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5km的雷达,监测点的分布情况如图,如果将雷达装置设在P点,每一个小格的边长为1km , 那么能被雷达监测到的最远点为( )
A、 , B、 , C、 , D、 ,6. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5km的雷达,监测点的分布情况如图,如果将雷达装置设在P点,每一个小格的边长为1km , 那么能被雷达监测到的最远点为( )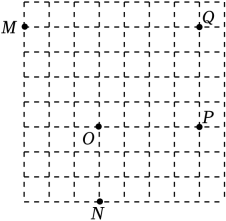 A、M点 B、N点 C、P点 D、Q点7. 二次函数的图象是抛物线 , 自变量与函数的部分对应值如下表:
A、M点 B、N点 C、P点 D、Q点7. 二次函数的图象是抛物线 , 自变量与函数的部分对应值如下表:x … -3 -2 -1 0 1 2 … y … 4 0 -2 -2 0 4 … 下列说法错误的是( )
A、抛物线的开口向上 B、抛物线的对称轴是 C、抛物线与轴的交点坐标为 D、二次函数的最小值为8. 两块完全相同的含角的直角三角板和重合在一起,将三角板绕直角顶点按逆时针方向旋转 , 如图所示.以下结论错误的是( )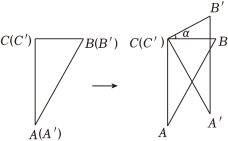 A、当时,与的交点恰好为中点.
A、当时,与的交点恰好为中点.
B、当时,恰好经过点 .
C、在旋转过程中,存在某一时刻,使得 .
D、在旋转过程中,始终存在 .二、填空题(本大题共8小题,共40.0分)
-
9. 方程x2=1的解是 .10. 在平面直角坐标系中,点关于原点对称的点的坐标为 .11. 写出一个开口向上,并且与y轴交于点(0,2)的抛物线的解析式 .12. 如图,将绕点顺时针旋转得到 , 边 , 相交于点 , 若 , 则 .
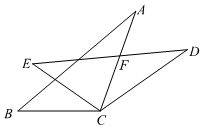 13. 在平面直角坐标系中,抛物线经过点 , 则填“”,“=”或“” .14. 若函数的图象与轴只有一个公共点,则 .15. 《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材,埋在壁中,不知大小.以锯锯之、深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,AB是⊙O的直径,弦CD⊥AB于点E , EB=1寸,CD=10寸,则直径AB长为 寸.
13. 在平面直角坐标系中,抛物线经过点 , 则填“”,“=”或“” .14. 若函数的图象与轴只有一个公共点,则 .15. 《九章算术》是中国传统数学重要的著作之一,其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材,埋在壁中,不知大小.以锯锯之、深一寸,锯道长一尺,问径几何?”用几何语言表达为:如图,AB是⊙O的直径,弦CD⊥AB于点E , EB=1寸,CD=10寸,则直径AB长为 寸.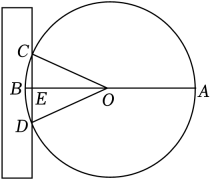 16. 我国三国时期的数学家赵爽在其所著的勾股圆方图注中记载了求一元二次方程正数解的几何解法.例如求方程的正数解的步骤为:
16. 我国三国时期的数学家赵爽在其所著的勾股圆方图注中记载了求一元二次方程正数解的几何解法.例如求方程的正数解的步骤为:将方程变形为;
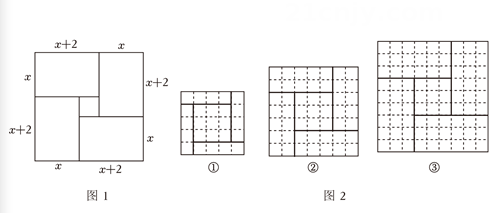
构造如图所示的大正方形,其面积是 , 其中四个全等的矩形面积分别为 , 中间的小正方形面积为;
大正方形的面积也可表示为四个矩形和一个小正方形的面积之和,即;
由此可得方程: , 则方程的正数解为 .
根据赵爽记载的方法,在图中的三个构图矩形的顶点均落在边长为的小正方形网格格点上中,能够得到方程的正数解的构图是只填序号 .
三、计算题(本大题共1小题,共5.0分)
-
17. 解方程:公式法
四、解答题(本大题共11小题,共65.0分。解答应写出文字说明,证明过程或演算步骤)
-
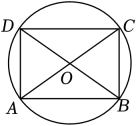
18. 如图,矩形ABCD的对角线AC , BD相交于点O .
求证:A , B , C , D四个点在以点O为圆心的同一个圆上.
 19. 已知:关于x的方程x2+4x+2m=0有两个不相等的实数根.(1)、求m的取值范围;(2)、若m为正整数,求此时方程的根.20. 在平面直角坐标系中,二次函数的图象经过点 , .
19. 已知:关于x的方程x2+4x+2m=0有两个不相等的实数根.(1)、求m的取值范围;(2)、若m为正整数,求此时方程的根.20. 在平面直角坐标系中,二次函数的图象经过点 , . (1)、求二次函数的解析式;(2)、画出二次函数的图象;(3)、当时,直接写出的取值范围.21. 如图,在中, , 且点的坐标为
(1)、求二次函数的解析式;(2)、画出二次函数的图象;(3)、当时,直接写出的取值范围.21. 如图,在中, , 且点的坐标为 (1)、画出绕点逆时针旋转后的;(2)、求点旋转到点所经过的路线长结果保留 .22. 某学校要设计校园“数学嘉年华”活动的项目介绍展板.如图,现有一块长25dm , 宽8dm的矩形展板,展示区域为全等的四个矩形,其中相邻的两个矩形展示区域之间及四周都留有宽度相同的空白区域.如果四个矩形展示区域的面积之和为120dm2 , 求空白区域的宽度.
(1)、画出绕点逆时针旋转后的;(2)、求点旋转到点所经过的路线长结果保留 .22. 某学校要设计校园“数学嘉年华”活动的项目介绍展板.如图,现有一块长25dm , 宽8dm的矩形展板,展示区域为全等的四个矩形,其中相邻的两个矩形展示区域之间及四周都留有宽度相同的空白区域.如果四个矩形展示区域的面积之和为120dm2 , 求空白区域的宽度.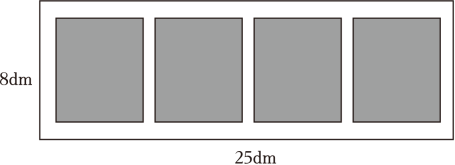 23. 如图,在等边中,是的中点,过点作 , 且 , 连接 .
23. 如图,在等边中,是的中点,过点作 , 且 , 连接 .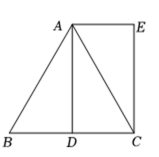 (1)、求证:四边形是矩形;(2)、连接交于点 , 连接若 , 求的长.24. 在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点(1,2).(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.25. 如图,一位足球运动员在一次训练中,从球门正前方8m的A处射门,已知球门高OB为2.44m , 球射向球门的路线可以看作是抛物线的一部分.当球飞行的水平距离为6m时,球达到最高点,此时球的竖直高度为3m .
(1)、求证:四边形是矩形;(2)、连接交于点 , 连接若 , 求的长.24. 在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过点(1,2).(1)、求这个一次函数的解析式;(2)、当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.25. 如图,一位足球运动员在一次训练中,从球门正前方8m的A处射门,已知球门高OB为2.44m , 球射向球门的路线可以看作是抛物线的一部分.当球飞行的水平距离为6m时,球达到最高点,此时球的竖直高度为3m .现以O为原点,如图建立平面直角坐标系.
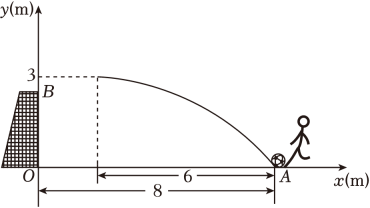 (1)、求抛物线表示的二次函数解析式;(2)、通过计算判断球能否射进球门(忽略其他因素);(3)、若运动员射门路线的形状、最大高度均保持不变,则他应该带球向正后方移动 米射门,才能让足球经过点O正上方2.25m处.26. 在平面直角坐标系中,点 , 在抛物线上,设该抛物线的对称轴为 .(1)、若 , 求的值;(2)、若 , 求的取值范围.27. 如图,在正方形中,点是线段延长线上一动点,连接 , 将线段绕点逆时针旋转得到线段 , 连接 , , 作直线交于点 .
(1)、求抛物线表示的二次函数解析式;(2)、通过计算判断球能否射进球门(忽略其他因素);(3)、若运动员射门路线的形状、最大高度均保持不变,则他应该带球向正后方移动 米射门,才能让足球经过点O正上方2.25m处.26. 在平面直角坐标系中,点 , 在抛物线上,设该抛物线的对称轴为 .(1)、若 , 求的值;(2)、若 , 求的取值范围.27. 如图,在正方形中,点是线段延长线上一动点,连接 , 将线段绕点逆时针旋转得到线段 , 连接 , , 作直线交于点 .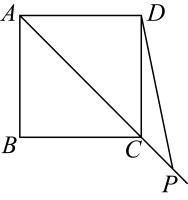 (1)、依题意补全图形;(2)、求证:;(3)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,给出如下定义:将图形绕直线上某一点顺时针旋转 , 得到图形 , 再将图形关于直线对称,得到图形此时称图形为图形关于点的“二次变换图形”已知点 .
(1)、依题意补全图形;(2)、求证:;(3)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,给出如下定义:将图形绕直线上某一点顺时针旋转 , 得到图形 , 再将图形关于直线对称,得到图形此时称图形为图形关于点的“二次变换图形”已知点 . (1)、若点 , 直接写出点关于点的“二次变换图形”的坐标;(2)、若点关于点的“二次变换图形”与点重合,求点的坐标;(3)、若点 , 半径为已知长度为的线段 , 其关于点的“二次变换图形”上的任意一点都在上或内,直接写出点的纵坐标的取值范围.
(1)、若点 , 直接写出点关于点的“二次变换图形”的坐标;(2)、若点关于点的“二次变换图形”与点重合,求点的坐标;(3)、若点 , 半径为已知长度为的线段 , 其关于点的“二次变换图形”上的任意一点都在上或内,直接写出点的纵坐标的取值范围.
-