天津市和平区2023-2024学年七年级上学期数学期中考试试卷

试卷更新日期：2023-11-24 类型：期中考试

进入出卷网下载

一、选择题（本大题共12小题，每小题2分，共24分．在每小题给出的四个选项中只有一项是符合题目要求的）．

1. 计算 $(- \frac{1}{2}) \times (- 2)$ 的结果等于（）

A、 $- \frac{5}{2}$ B、 $- 1$ C、 $\frac{1}{4}$ D、1

查看试题解析
2. 用四舍五入法取近似数0.05019（精确到0.001）的结果是（）

A、0.05 B、0.050 C、0.0501 D、0.051

查看试题解析
3. 据 $2023$ 年 $5$ 月 $21$ 日《天津日报》报道，在天津举办的第七届世界智能大会通过“百网同播、万人同屏、亿人同观”，全球网友得以共享高端思想盛宴，总浏览量达到 $935000000$ 人次，将数据 $935000000$ 用科学记数法表示应为（）

A、 $0.935 \times 1 0^{9}$ B、 $9.35 \times 1 0^{8}$ C、 $93.5 \times 1 0^{7}$ D、 $935 \times 1 0^{6}$

查看试题解析
4. 下列各组数中，互为倒数的是（）

A、1与 $- 1$ B、 $- \frac{1}{3}$ 与3 C、 $- 5$ 与 $- \frac{1}{5}$ D、 $- 3$ 与 $| - 3 |$

查看试题解析
5. 下列说法正确的是（）

A、 $- \frac{π x^{2} y}{3}$ 的系数是 $- \frac{1}{3}$ B、 $- 5 a^{2} b + 3 a b^{2} - 2$ 的常数项是2 C、 $- 3 a^{2} b^{4} c$ 与 $\frac{1}{2} b^{4} c a^{2}$ 是同类项 D、 $3^{2} x^{2} y + 2 x y - 7$ 是五次三项式

查看试题解析
6. 如果单项式 $- x {y^{b}}^{+ 1}$ 与 $\frac{1}{2} x^{a + 2} y^{3}$ 的和仍然是一个单项式，则 $a + b$ 的值为（）

A、 $1$ B、 $- 1$ C、 $- 2$ D、 $2$

查看试题解析
7. 根据等式的性质，下列各式变形正确的是（）

A、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ B、若 $a c = b c$ ，则 $a = b$ C、若 $a^{2} = b^{2}$ ，则 $a = b$ D、若 $- \frac{1}{3} x = 6$ ，则 $x = - 2$

查看试题解析
8. 下列运算结果正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $7 x^{2} y - 4 x y^{2} = 3 x^{2} y$ C、 $a - b - (a + b) = 0$ D、 $3 a + 2 b - 2 (a - b) = a + 4 b$

查看试题解析
9. 一个两位数，十位上的数是 $1$ ，个位上的数是 $x$ ．把 $1$ 与 $x$ 对调，新两位数比原两位数大 $18$ ．根据题意列出的方程为（）．

A、 $10 x + 1 - 10 + x = 18$ B、 $10 x + 1 - (10 + x) = 18$ C、 $10 + x - 10 x + 1 = 18$ D、 $10 + x - (10 x + 1) = 18$

查看试题解析
10. 王阿姨在甲批发市场以每件 $x$ 元的价格进了30件衬衫，又在乙批发市场以每件 $y$ 元 $(x > y)$ 的价格进了50件同样的衬衫．如果以每件 $\frac{x + y}{2}$ 元的价格将衬衫全部卖出，那么王阿姨（）

A、盈利了 B、亏损了 C、不盈也不亏 D、盈亏不能确定

查看试题解析
11. 对于有理数 $a$ ，下列比较大小正确的是（）

A、当 $0 < a < 1$ 时， $a < a^{2} < a^{3}$ B、当 $- 1 < a < 0$ 时， $a < a^{2} < a^{3}$ C、当 $a$ 为任意有理数时，均有 $a < a^{2} < a^{3}$ D、当 $a < - 1$ 时， $a^{3} < a < a^{2}$

查看试题解析
12. 代数式|x﹣1|﹣|x+2|的最大值为a，最小值为b，下列说法正确的是（）

A、a＝3，b＝0 B、a＝0，b＝﹣3 C、a＝3，b＝﹣3 D、a＝3，b 不存在

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）．

13. 如果水位升高 $3 m$ 时记作 $+ 3 m$ ，那么水位下降 $5 m$ 时记作 $m$ ．

查看试题解析
14. 如图，将一刻度尺放在数轴上（数轴的单位长度是 $1 c m$ ），刻度尺上“ $0 c m$ ”和“ $3 c m$ ”分别对应数轴上的3和0，那么刻度尺上“ $3.6 c m$ ”对应数轴上的数为．

查看试题解析
15. 若 $| x - 2 | + (y + 1)^{2} = 0$ ，那么 $x + y =$ ．

查看试题解析
16. 当 $a + b = 3$ 时，代数式 $2 (a + 2 b) - (3 a + 5 b) + 5$ 的值为．

查看试题解析
17. 关于 $x$ 的一元一次方程 $2 x^{a + 2} + m = 4$ 的解为 $x = 1$ ，则 $a^{m}$ 的值为．

查看试题解析
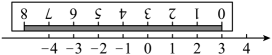18. 如下图所示，对于任意正整数，若 $n$ 为奇数则乘3再加1，若 $n$ 为偶数则除以2，在这样一次变化下，我们得到一个新的自然数．在1937年 $L o t h a r C o l l a t z$ 提出了一个问题：如此反复这种变换，是否对于所有的正整数，最终都能变换到1呢？这就是数学中著名的“考拉兹猜想”．如果某个正整数通过上述变换能变成1，我们就把第一次变成1时所经过的变换次数称为它的路径长，例如5经过5次变成1，则路径长 $m = 5$ ．若输入数 $n$ ，路径长为 $m$ ，当 $m = 7$ 时， $n$ 的所有可能值有个，其中最小值为．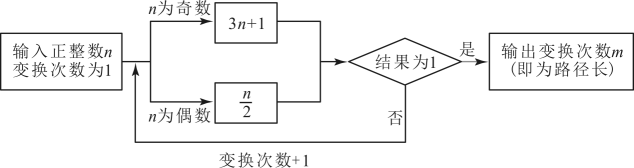

查看试题解析

三、解答题（本大题共7小题，共58分．解答应写出文字说明、演算步骤或推理过程）

19. 如图是一条不完整的数轴，相邻两点之间相距1个单位长度，点A表示的数是 $- 3$ ．

(1)、补全数轴，并指出点 $B$ 所表示的数是；

(2)、在数轴上表示下列各数，并把这些数按从小到大的顺序连接起来．
2.5， $- (- 2)^{2} ， - 1 \frac{1}{2} ， | - 5 | ， - (- 1) ， - | - 2 |$ ．

查看试题解析
20. 计算：

(1)、 $(- 0.5) - (- 3.2) + (+ 2.8) - (+ 6.5)$ ；

(2)、 $(- 155 \frac{15}{38}) \div 5$ ；

(3)、 $17 - 8 \div (- 2) + 4 \times (- 5) - 1 \div 2 \times \frac{1}{2}$ ；

(4)、 $[(- 1)^{2023} + (- 3)^{2} \times (\frac{1}{3} - \frac{1}{2})] \times \frac{3}{10} \div (- 0 . 1^{2})$ ．

查看试题解析
21. 如图，要围一个长方形菜园 $A B C D$ ，共中一边 $A D$ 是墙（墙足够长），其余的三边 $A B$ ， $B C$ ， $C D$ 用篱笆，已知 $B C$ 长为 $(x y^{2} + 5 x - 2 y + 14)$ 米， $A B$ 的长比 $B C$ 少 $(\frac{3}{2} x y^{2} + \frac{15}{2} x - 3 y + 1)$ 米．

(1)、用 $x$ ， $y$ 表示 $A B$ 的长；

(2)、若安装篱笆的造价是每米 $80$ 元，当 $x$ ， $y$ 的取值发生变化时，总造价发生变化吗？为什么？

查看试题解析
22. 已知关于 $x ， y$ 的多项式 $2 (m x^{2} - 2 y^{2}) - (x - 2 y)$ 与 $x - n y^{2} - 2 x^{2}$ 的差不含 $x^{2}$ 和 $y^{2}$ 项．

(1)、求 $m ， n$ 的值；

(2)、在（1）的条件下，化简求值 $(4 m^{2} n - 3 m n^{2}) - 2 (m^{2} n + m n^{2})$ ．

查看试题解析
23. 将从1开始的连续自然数按图规律排列：规定位于第3行，第2列的自然数 $10$ 记为 $(3 ， 2)$ ，自然数14记为 $(4 ， 3)$ ……
按此规律，回答下列问题：

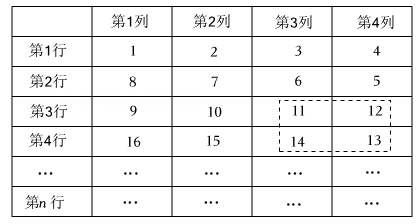(1)、记为 $(6 ， 3)$ 表示的自然数是；

(2)、自然数 $2023$ 记为；

(3)、用一个正方形方框在第 $3$ 列和第4列中任意框四个数，这四个数的和能为 $738$ 吗？如果能，求出框出的四个数中最小的数；如果不能，请写出理由．

查看试题解析
24. 在数轴上，点 $A$ ， $B$ 分别表示数 $a$ ， $b$ ．点 $C$ 在 $A$ ， $B$ 之间，点 $C$ 表示数 $c$ ．

(1)、若 $a = 2$ ， $b = 6$ ，则 $A$ ， $B$ 之间的距离是；

(2)、若 $A C = C B$ ，则点 $C$ 叫做线段 $A B$ 的中点．
①若 $a = 2$ ， $b = - 6$ ，则 $c =$ ；
②若 $c = - 1$ ，将点 $A$ 向右平移10个单位，恰好与点 $B$ 重合，则 $a =$ ；
③一般地，将 $c$ 用 $a$ 和 $b$ 表示出来为 $c =$ ；

(3)、若 $A C = λ C B$ （其中 $λ > 0$ ）．
①当 $a = - 2$ ， $b = 4$ ， $λ = \frac{1}{2}$ 时， $c =$ ；
②一般地，将 $c$ 用 $a$ ， $b$ 和 $λ$ 表示出来为 $c =$ ．

查看试题解析
25.

(1)、小天用下表记录九月的流量使用情况，每个时间段以5 $G B$ 为标准，超出部分记为正数，不足部分记为负数，（单位： $M B$ ）．
1日-5日 6日-10日 11日-15日 16日-20日 21日-25日 26日-30日
200 -100 100 -100 212 200
说明：数据流量 $1 G B = 1024 M B$ ．
请你计算：小天九月份共用使用了多少流量？

(2)、某通讯公司推出 $A ， B$ 两种话费套餐，套餐详情如下表：
月基本费/元主叫限定时间/min 主叫超时费/（元/min）被叫免费数据流量/GB
A a 600 0.15 免费 15
B 99 500 0.15 免费 20
已知小天使用 $A$ 套餐，某月主叫时间为 $800 m i n$ ，使用流量 $14.5 G B$ ，共产生109元月结话费（月结话费=月基本费+主叫超时费+流量超出费），求 $a$ 的值；

(3)、在（2）的条件下，通讯公司对 $A ， B$ 两种话费套餐做了如下补充说明：
①流量超出后， $A$ 套餐按5元 $1 G B$ 标准收取，不满 $1 G B$ 按0.005元/ $M B$ 收取．
②流量超出后， $B$ 套餐按5元 $1 G B$ 标准收取，满15元后按3元 $1 G B$ 收取，不满 $1 G B$ 按 $1 G B$ 计算．
请你根据以上信息，帮助小天解决下列问题：
①小天估计十月份主叫时间不超过 $500 m i n$ ，所用流量是 $x G B$ （ $x > 20$ 且 $x$ 是整数）．用含 $x$ 的代数式表示使用 $A ， B$ 两种套餐各需要多少钱？
②经过查询，小天发现，十月份主叫时长为 $700 m i n$ ，使用的总流量与九月份相同．请你帮助小天计算并判断选择哪种套餐更合算．

查看试题解析

1日-5日	6日-10日	11日-15日	16日-20日	21日-25日	26日-30日
200	-100	100	-100	212	200

月基本费/元	主叫限定时间/min	主叫超时费/（元/min）	被叫	免费数据流量/GB
A	a	600	0.15	免费	15
B	99	500	0.15	免费	20